Na rysunku przedstawiono bryłę, której podstawą jest kwadrat a ściany boczne są prostopadłe do płaszczyzny podstawy. Wymiary bryły podane są na rysunku.
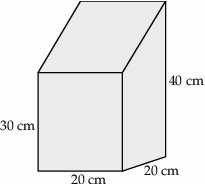
Oblicz objętość tej bryły.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Na rysunku przedstawiono bryłę, której podstawą jest kwadrat a ściany boczne są prostopadłe do płaszczyzny podstawy. Wymiary bryły podane są na rysunku.

Oblicz objętość tej bryły.
Trójkąt równoramienny o kącie 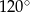 i ramieniu długości 6 obrócono względem zewnętrznej wysokości, otrzymując wydrążoną bryłę. Oblicz objętość tej bryły.
i ramieniu długości 6 obrócono względem zewnętrznej wysokości, otrzymując wydrążoną bryłę. Oblicz objętość tej bryły.
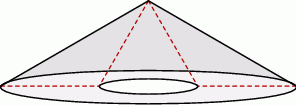
Środki ścian sześcianu są wierzchołkami innej bryły – ośmiościanu foremnego (zobacz rysunek).
Oblicz objętość tego ośmiościanu jeżeli krawędź sześcianu ma długość  .
.
Trapez prostokątny o podstawach długości 4 i 5 oraz kącie ostrym równym 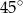 obraca się wokół krótszej podstawy. Oblicz objętość otrzymanej bryły.
obraca się wokół krótszej podstawy. Oblicz objętość otrzymanej bryły.
W kostce mającej kształt sześcianu o boku 1 dm ścięto wszystkie naroża w ten sposób ze wszystkie krawędzie nowopowstałej bryły mają tę samą długość. Obliczyć objętość otrzymanej bryły.
Trójkąt równoramienny o podstawie długości 6 cm i ramionach długości 5 cm obracamy wokół jednego z ramion. Otrzymaną w ten sposób bryłę dzielimy na dwa stożki. Podaj długość promienia podstawy i długość tworzącej każdego z tych stożków.
Oblicz długość przeciwprostokątnej trójkąta prostokątnego, wiedząc, że objętość brył powstałych z obrotu tego trójkąta wokół przyprostokątnych wynoszą odpowiednio 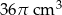 i
i 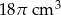 .
.
Trójkąt prostokątny o przyprostokątnych 15 i 20 obraca się wokół przeciwprostokątnej. Oblicz objętość i pole powierzchni całkowitej tej bryły.
Trapez równoramienny o podstawach długości 14 cm i 26 cm oraz o wysokości 6 cm obraca się wokół swojej osi symetrii. Oblicz objętość otrzymanej bryły.
W trójkącie ostrokątnym 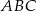 mamy
mamy  , zaś
, zaś  . Oblicz objętość bryły powstałej z obrotu trójkąta
. Oblicz objętość bryły powstałej z obrotu trójkąta  wokół prostej zawierającej bok
wokół prostej zawierającej bok 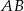 .
.
Romb o kącie ostrym 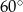 , obraca się wokół boku. Oblicz pole powierzchni i objętość otrzymanej bryły wiedząc że długość boku rombu jest równa
, obraca się wokół boku. Oblicz pole powierzchni i objętość otrzymanej bryły wiedząc że długość boku rombu jest równa  .
.
Kapsuła lądownika ma kształt stożka zakończonego w podstawie półkulą o tym samym promieniu co promień podstawy stożka. Wysokość stożka jest o 1 m większa niż promień półkuli. Objętość stożka stanowi  objętości całej kapsuły. Oblicz objętość kapsuły lądownika.
objętości całej kapsuły. Oblicz objętość kapsuły lądownika.
Z drewnianego prostopadłościanu o objętości 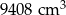 i podstawie będącej kwadratem o boku 14 cm, wycięto ostrosłup prawidłowy czworokątny o wysokości równej połowie najdłuższej krawędzi prostopadłościanu. Otrzymano w ten sposób bryłę, której widok z dwóch stron przedstawiono na rysunku. Oblicz pole powierzchni całkowitej otrzymanej bryły.
i podstawie będącej kwadratem o boku 14 cm, wycięto ostrosłup prawidłowy czworokątny o wysokości równej połowie najdłuższej krawędzi prostopadłościanu. Otrzymano w ten sposób bryłę, której widok z dwóch stron przedstawiono na rysunku. Oblicz pole powierzchni całkowitej otrzymanej bryły.
Trójkąt o bokach długości 5, 8 i 9 obraca się dookoła najdłuższego boku. Oblicz objętość powstałej bryły.
Trójkąt o bokach długości 3, 5 i 7 obraca się dookoła najdłuższego boku. Oblicz objętość powstałej bryły.
Trójkąt o bokach długości 17, 28 i 33 obraca się dookoła najdłuższego boku. Oblicz objętość powstałej bryły.
Trapez prostokątny obraca się wokół boku tworzącego z podstawami kąty proste. Podstawy trapezu mają długość odpowiednio 10 cm i 7 cm. Pole trapezu wynosi 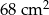 . Oblicz objętość otrzymanej bryły.
. Oblicz objętość otrzymanej bryły.
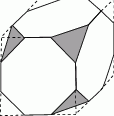
W dwudziestościanie foremnym odcięto płaszczyznami przechodzącymi przez środki krawędzi każdy z narożników. Ile ścian ma powstała w ten sposób bryła i jakimi są one wielokątami?
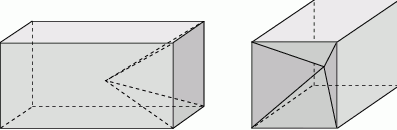
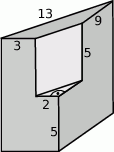
Spawacz ma wykonać z blachy konstrukcję, która powstaje przez wycięcie z graniastosłupa prostego trójkątnego innego graniastosłupa prostego trójkątnego. Wymiary elementów są podane na rysunku.
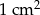 .
.Trójkąt prostokątny o przyprostokątnych długości 12 i 7 obraca się wokół przeciwprostokątnej. Oblicz promień kuli wpisanej w otrzymaną bryłę.
Kwadrat o boku długości 2 cm obraca się wokół swojej przekątnej. Oblicz objętość i pole powierzchni otrzymanej bryły.
Trzy wychodzące z jednego wierzchołka krawędzie równoległościanu są równe 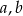 i
i  . Krawędzie
. Krawędzie  i
i 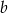 są prostopadłe, a krawędź
są prostopadłe, a krawędź  tworzy z każdą z nich kąt ostry
tworzy z każdą z nich kąt ostry  . Oblicz objętość równoległościanu.
. Oblicz objętość równoległościanu.
