Rzucamy monetą tak długo, aż dwa razy z rzędu upadnie tą samą stroną. Jakie jest prawdopodobieństwo, że zdarzenie skończy się najwyżej po  rzutach?
rzutach?
/Szkoła średnia/Prawdopodobieństwo
Rzucamy trzy razy symetryczną sześcienną kostką do gry, która na każdej ściance ma inną liczbę oczek – od jednego oczka do sześciu oczek. Oblicz prawdopodobieństwo zdarzenia 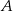 polegającego na tym, że co najmniej jeden raz wypadnie ścianka z dwoma oczkami.
polegającego na tym, że co najmniej jeden raz wypadnie ścianka z dwoma oczkami.
Rzucamy 6 razy symetryczną 6-ścienną kostką do gry. Oblicz prawdopodobieństwo
- otrzymania co najmniej raz szóstki;
- otrzymania co najwyżej raz szóstki.
Rzucamy sześcienną kostką do gry. Jakie jest prawdopodobieństwo, że wypadną co najmniej dwa oczka.
Rzucamy sześcienną kostką do gry. Jakie jest prawdopodobieństwo, że wypadnie liczba pierwsza?
Rzucamy sześcienną kostką do gry. Jakie jest prawdopodobieństwo, że wypadnie liczba od 1 do 6.
Ze zbioru wszystkich liczb naturalnych dwucyfrowych losujemy kolejno dwa razy po jednej liczbie bez zwracania. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma wylosowanych liczb będzie równa 30. Wynik zapisz w postaci ułamka zwykłego nieskracalnego.
Ze zbioru wszystkich liczb naturalnych dwucyfrowych losujemy kolejno dwa razy po jednej liczbie bez zwracania. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że jedna z wylosowanych liczb jest o 85 większa od drugiej. Wynik zapisz w postaci ułamka zwykłego nieskracalnego.
Urzędnik bankowy wie, że 12% kredytobiorców hipotecznych traci pracę i przestaje spłacać pożyczkę w ciągu 5 lat. Wie też, że 20% kredytobiorców hipotecznych traci pracę w ciągu 5 lat. Przy założeniu, że kredytobiorca hipoteczny stracił pracę, jakie jest prawdopodobieństwo, iż przestanie spłacać pożyczkę.
Ze zbioru 26 liter alfabetu łacińskiego 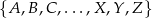 losujemy bez zwracania trzy razy jedną literę. Oblicz prawdopodobieństwo tego, że wśród wylosowanych liter znalazła się przynajmniej jedna z liter
losujemy bez zwracania trzy razy jedną literę. Oblicz prawdopodobieństwo tego, że wśród wylosowanych liter znalazła się przynajmniej jedna z liter 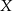 ,
, 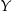 lub
lub 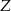 .
.
Na sześciu jednakowych kartkach napisano liczby: 1, 10, 100, 1000, 10000, 100000. Z tych kartek losujemy kolejno bez zwracania trzy. Oblicz prawdopodobieństwo, że suma wylosowanych liczb tworzy liczbę podzielną przez cztery.
Ze zbioru pięciu liczb 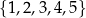 losujemy bez zwracania kolejno dwa razy po jednej liczbie. Oblicz prawdopodobieństwo zdarzenia
losujemy bez zwracania kolejno dwa razy po jednej liczbie. Oblicz prawdopodobieństwo zdarzenia 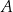 polegającego na tym, że obie wylosowane liczby są nieparzyste.
polegającego na tym, że obie wylosowane liczby są nieparzyste.
Ze zbioru wszystkich liczb naturalnych trzycyfrowych losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia 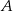 polegającego na tym, że wylosowana liczba jest podzielna przez 4 oraz ma dwie cyfry nieparzyste.
polegającego na tym, że wylosowana liczba jest podzielna przez 4 oraz ma dwie cyfry nieparzyste.
Wzór funkcji 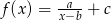 tworzymy w następujący sposób. Ze zbioru
tworzymy w następujący sposób. Ze zbioru
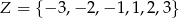
losujemy kolejno 3 liczby (bez zwracania); pierwsza z wylosowanych liczb jest równa współczynnikowi  , druga – współczynnikowi
, druga – współczynnikowi 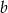 , trzecia – współczynnikowi
, trzecia – współczynnikowi  . Oblicz prawdopodobieństwo zdarzeń:
. Oblicz prawdopodobieństwo zdarzeń:
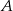 – funkcja
– funkcja 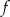 jest funkcją malejącą w każdym ze zbiorów
jest funkcją malejącą w każdym ze zbiorów 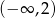 oraz
oraz 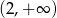 ;
; 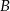 – miejscem zerowym funkcji
– miejscem zerowym funkcji 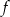 jest 0.
jest 0. 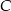 – funkcja
– funkcja 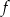 jest funkcją malejącą w każdym ze zbiorów
jest funkcją malejącą w każdym ze zbiorów 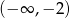 oraz
oraz 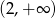 ;
;
Ze zbioru liczb 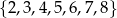 losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia
losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 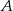 polegającego na wylosowaniu liczb, z których pierwsza jest o 2 mniejsza od drugiej.
polegającego na wylosowaniu liczb, z których pierwsza jest o 2 mniejsza od drugiej.
Ze zbioru sześciu liczb 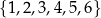 losujemy ze zwracaniem kolejno dwa razy po jednej liczbie. Oblicz prawdopodobieństwo zdarzenia
losujemy ze zwracaniem kolejno dwa razy po jednej liczbie. Oblicz prawdopodobieństwo zdarzenia 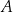 polegającego na tym, że pierwsza wylosowana liczba będzie większa od drugiej wylosowanej liczby.
polegającego na tym, że pierwsza wylosowana liczba będzie większa od drugiej wylosowanej liczby.
Ze zbioru liczb 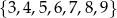 losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia
losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 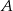 polegającego na wylosowaniu liczb, z których pierwsza jest o 3 większa od drugiej.
polegającego na wylosowaniu liczb, z których pierwsza jest o 3 większa od drugiej.
Na osi liczbowej każde dwie spośród 1000 kolejnych liczb naturalnych 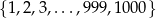 połączono odcinkiem. Następnie wybrano losowo jeden z tych odcinków. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że do wylosowanego odcinka należy liczba 307 (może też być jednym z jego końców). Wynik podaj w postaci ułamka nieskracalnego.
połączono odcinkiem. Następnie wybrano losowo jeden z tych odcinków. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że do wylosowanego odcinka należy liczba 307 (może też być jednym z jego końców). Wynik podaj w postaci ułamka nieskracalnego.
Ze zbioru wszystkich liczb naturalnych dwucyfrowych losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia 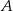 polegającego na tym, że wylosowana liczba ma w zapisie dziesiętnym cyfrę dziesiątek, która należy do zbioru
polegającego na tym, że wylosowana liczba ma w zapisie dziesiętnym cyfrę dziesiątek, która należy do zbioru 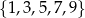 , i jednocześnie cyfrę jedności, która należy do zbioru
, i jednocześnie cyfrę jedności, która należy do zbioru 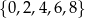 .
.
Ze zbioru wszystkich liczb naturalnych dwucyfrowych losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia 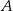 polegającego na tym, że wylosowana liczba ma w zapisie dziesiętnym nieparzystą cyfrę jedności, oraz parzystą cyfrę dziesiątek.
polegającego na tym, że wylosowana liczba ma w zapisie dziesiętnym nieparzystą cyfrę jedności, oraz parzystą cyfrę dziesiątek.
Ze zbioru 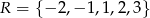 losujemy najpierw jedną liczbę i oznaczamy ją jako
losujemy najpierw jedną liczbę i oznaczamy ją jako  . Następnie z pozostałych liczb losujemy drugą liczbę i oznaczamy ją jako
. Następnie z pozostałych liczb losujemy drugą liczbę i oznaczamy ją jako 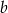 . Liczby
. Liczby  i
i 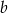 są współczynnikami funkcji kwadratowej
są współczynnikami funkcji kwadratowej 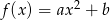 . Oblicz prawdopodobieństwo zdarzenia:
. Oblicz prawdopodobieństwo zdarzenia:
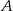 – funkcja
– funkcja 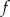 jest malejąca w zbiorze
jest malejąca w zbiorze 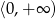 ,
, 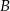 – funkcja
– funkcja 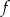 ma dwa różne miejsca zerowe.
ma dwa różne miejsca zerowe.
Ze zbioru 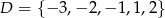 losujemy najpierw jedną liczbę i oznaczamy ją jako
losujemy najpierw jedną liczbę i oznaczamy ją jako  . Następnie z pozostałych liczb losujemy drugą liczbę i oznaczamy ją jako
. Następnie z pozostałych liczb losujemy drugą liczbę i oznaczamy ją jako 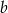 . Liczby
. Liczby  i
i 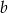 są współczynnikami funkcji kwadratowej
są współczynnikami funkcji kwadratowej 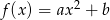 . Oblicz prawdopodobieństwo zdarzenia:
. Oblicz prawdopodobieństwo zdarzenia:
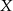 – funkcja
– funkcja 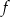 jest malejąca w zbiorze
jest malejąca w zbiorze 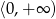 ,
, 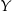 – funkcja
– funkcja 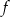 ma dwa różne miejsca zerowe.
ma dwa różne miejsca zerowe.
Ze zbioru liczb: 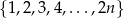 , gdzie
, gdzie 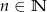 i
i 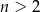 losujemy kolejno trzy razy po jednej liczbie bez zwracania. Niech
losujemy kolejno trzy razy po jednej liczbie bez zwracania. Niech 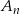 oznacza zdarzenie: iloczyn wylosowanych liczb jest liczbą nieparzystą, a
oznacza zdarzenie: iloczyn wylosowanych liczb jest liczbą nieparzystą, a 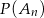 prawdopodobieństwo zajścia zdarzenia
prawdopodobieństwo zajścia zdarzenia 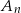 . Oblicz:
. Oblicz: 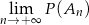 .
.
W fabryce zainstalowano 3 urządzenia 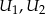 i
i 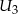 niezależnie wykrywające awarie. Prawdopodobieństwo wykrycia awarii przez kolejne urządzenia wynoszą
niezależnie wykrywające awarie. Prawdopodobieństwo wykrycia awarii przez kolejne urządzenia wynoszą 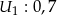 ,
, 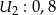 ,
, 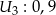 . Oblicz prawdopodobieństwo wykrycia awarii przez:
. Oblicz prawdopodobieństwo wykrycia awarii przez:
- dokładnie 2 urządzenia,
- co najmniej 1 urządzenie.
Rzucamy jednocześnie kostką i sześcioma symetrycznymi monetami. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, liczba otrzymanych oczek na kostce jest równa łącznej liczbie otrzymanych orłów na monetach.
Losujemy jedną kartę spośród wszystkich króli z talii oraz jedną kartę spośród wszystkich dam. Jakie jest prawdopodobieństwo otrzymania w ten sposób dwóch kart tego samego koloru np. dwóch treflii lub dwóch kar?
W pojemniku znajduje się 28 kul, przy czym  z nich to kule białe, a pozostałe to kule czarne. Z pojemnika losujemy dwa razy po jednej kuli ze zwracaniem. Dla jakiej liczby
z nich to kule białe, a pozostałe to kule czarne. Z pojemnika losujemy dwa razy po jednej kuli ze zwracaniem. Dla jakiej liczby  prawdopodobieństwo wylosowania jednej kuli białej i jednej czarnej jest największe?
prawdopodobieństwo wylosowania jednej kuli białej i jednej czarnej jest największe?

