Z talii 52 kart w czterech kolorach wybieramy losowo 2 karty. Oblicz prawdopodobieństwo, że wybrane karty to król i as, przy założeniu, że wybrane karty mają różne kolory.
/Szkoła średnia/Prawdopodobieństwo
W pierwszej urnie umieszczono 3 kule białe i 5 kul czarnych, a w drugiej urnie 7 kul białych i 4 kule czarne. Losujemy jedną kulę z pierwszej urny i przekładamy ją do drugiej urny. Następnie losujemy dwie kule z urny drugiej. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że dwie kule wylosowane z drugiej urny są w różnych kolorach.
Ze zbioru liczb trzycyfrowych losujemy jedną liczbę. Jakie jest prawdopodobieństwo, że iloczyn cyfr wylosowanej liczby jest liczbą parzystą?
W urnie jest dziesięć kul: 4 białe, 3 czarne, 2 zielone i 1 niebieska. Losujemy jednocześnie trzy kule z urny. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wśród wylosowanych kul nie ma kul w tym samym kolorze. Wynik przedstaw w postaci ułamka zwykłego nieskracalnego.
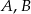 są zdarzeniami losowymi zawartymi w
są zdarzeniami losowymi zawartymi w 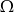 . Wykaż, że jeżeli
. Wykaż, że jeżeli 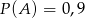 i
i 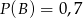 , to
, to 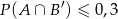 (
(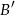 oznacza zdarzenie przeciwne do zdarzenia
oznacza zdarzenie przeciwne do zdarzenia 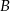 ).
).
Na stacji czekało na pociąg 10 pasażerów. Przyjechał pociąg składający się z 7 wagonów. Jakie jest prawdopodobieństwo, że wszyscy pasażerowie wsiedli tylko do dwóch wagonów, jeśli pasażerowie losowo wybierali wagony?
Listonosz losowo rozmieszcza 4 listy w 6 skrzynkach na listy. Jakie jest prawdopodobieństwo, że przynajmniej dwa listy znajdą się w tej samej skrzynce?
Oblicz prawdopodobieństwo otrzymania przez brydżystę asa ustalonego koloru.
Oblicz prawdopodobieństwo otrzymania przez brydżystę dokładnie jednego asa.
Oblicz prawdopodobieństwo otrzymania przez brydżystę dokładnie trzech asów.
Oblicz prawdopodobieństwo otrzymania przez brydżystę dokładnie jednego asa i dokładnie jednego króla.
Oblicz prawdopodobieństwo otrzymania przez brydżystę czterech asów.
Oblicz prawdopodobieństwo otrzymania przez brydżystę dokładnie dwóch asów.
Sześciu pasażerów wsiada do tramwaju złożonego z trzech wagonów. Każdy losowo wybiera wagon. Jakie jest prawdopodobieństwo, że wszyscy wsiądą do jednego wagonu?
Sześciu pasażerów wsiada do tramwaju złożonego z trzech wagonów. Każdy losowo wybiera wagon. Jakie jest prawdopodobieństwo, że pasażerowie znajdują się w dokładnie dwóch wagonach?
Rzucamy dwa razy kostką do gry. Niech 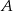 oznacza zdarzenie suma wyrzuconych oczek jest większa od 7, a
oznacza zdarzenie suma wyrzuconych oczek jest większa od 7, a 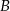 zdarzenie, że iloczyn wyrzuconych oczek jest mniejszy od 48.
zdarzenie, że iloczyn wyrzuconych oczek jest mniejszy od 48.
- Oblicz
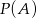 i
i 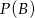 .
. - Sprawdź czy zdarzenia
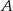 i
i 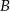 są niezależne,
są niezależne, - Oblicz
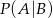 i
i 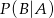 .
.
Mamy dwie talie kart po 24 karty. Z pierwszej talii losujemy jedną kartę i nie oglądając jej wkładamy do drugiej talii. Następnie z drugiej talii losujemy jedną kartę.
- Jakie jest prawdopodobieństwo wylosowania króla, jeżeli wiemy, że z pierwszej talii przełożono do drugiej trefla?
- Obliczyć prawdopodobieństwo, że wylosowana karta jest kierem.
- Wylosowana karta okazała się kierem. Jakie jest prawdopodobieństwo tego, że z pierwszej talii także został wylosowany kier?
Test na rzadką chorobę, którą dotknięta jest średnio jedna osoba na tysiąc, daje fałszywą pozytywną odpowiedź w 5% przypadków (u osoby chorej daje zawsze odpowiedź pozytywną). Jaka jest szansa, że osoba, u której test dał odpowiedź pozytywną, jest faktycznie chora?
Na stole stoją dwa identyczne koszyki, w których znajduje się po 15 jednakowej wielkości piłeczek. Piłeczki są w kolorze żółtym i czerwonym. W obu koszykach liczba piłeczek żółtych jest taka sama. Z każdego koszyka losujemy jedną piłeczkę. Ile powinno być w każdym koszyku żółtych piłeczek, aby prawdopodobieństwo wylosowania piłeczek różnych kolorów było największe?
W urnie znajduje się 40 losów, wśród których są tylko losy wygrywające i przegrywające. Z urny wyciągamy dwa losy. Niech 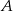 oznacza zdarzenie – wylosowano dwa losy wygrywające, zaś
oznacza zdarzenie – wylosowano dwa losy wygrywające, zaś 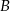 zdarzenie – wylosowano jeden los wygrywający i jeden przegrywający.
zdarzenie – wylosowano jeden los wygrywający i jeden przegrywający.
- Oblicz ile jest losów wygrywających, jeżeli
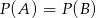 .
. - Sprawdź, które zdarzenie jest bardziej prawdopodobne: zdarzenie
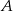 , czy zdarzenie
, czy zdarzenie 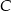 – wylosowano dwa losy przegrywające
– wylosowano dwa losy przegrywające
Wiadomo, że 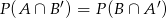 ,
, 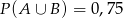 ,
, 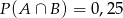 . Oblicz:
. Oblicz: 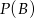 i
i 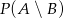 .
.
Ze zbioru 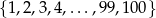 wybieramy cztery różne liczby i obliczamy ich sumę. Oblicz jakie jest prawdopodobieństwo tego, że suma wybranych liczb jest nieparzysta. Wynik podaj w postaci ułamka nieskracalnego.
wybieramy cztery różne liczby i obliczamy ich sumę. Oblicz jakie jest prawdopodobieństwo tego, że suma wybranych liczb jest nieparzysta. Wynik podaj w postaci ułamka nieskracalnego.
O zdarzeniach losowych 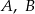 wiadomo, że:
wiadomo, że: 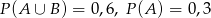 i
i 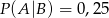 . Oblicz prawdopodobieństwo warunkowe
. Oblicz prawdopodobieństwo warunkowe 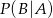 .
.
O zdarzeniach losowych 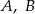 wiadomo, że:
wiadomo, że: 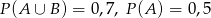 i
i 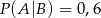 . Oblicz prawdopodobieństwo warunkowe
. Oblicz prawdopodobieństwo warunkowe 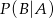 .
.
Ze zbioru liczb trzycyfrowych, które nie mają dwóch takich samych cyfr losujemy jedną liczbę. Jakie jest prawdopodobieństwo otrzymania liczby, której iloczyn cyfr jest liczbą niezerową podzielną przez 7?
Przy okrągłym stole ustawiono 10 krzeseł i posadzono 10 osób, wśród których są osoby 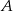 i
i 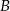 . Oblicz prawdopodobieństwo, że osoby
. Oblicz prawdopodobieństwo, że osoby 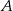 i
i 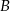 będą siedziały obok siebie.
będą siedziały obok siebie.
W pojemniku umieszczono 50 drewnianych klocków, przy czym każdy klocek ma kształt sześcianu lub kuli, oraz każdy klocek jest czerwony lub niebieski. Wiadomo, że w pojemniku znajduje się dokładnie 15 czerwonych sześcianów, 18 klocków niebieskich i 31 klocków mających kształt kuli. Z pojemnika losowo wybieramy jeden klocek. Oblicz prawdopodobieństwo, że wylosowany klocek jest niebieską kulą.

