W urnie są 3 kule białe, 4 czarne i 5 zielonych. Losujemy ze zwracaniem 3 kule. Oblicz prawdopodobieństwo tego, że wśród wylosowanych kul będą kule biała i czarna.
/Szkoła średnia/Prawdopodobieństwo
Do worka wrzucono 50 losów loteryjnych w tym 15 wygrywających. Wyciągamy dwa losy. Jakie jest prawdopodobieństwo, że oba losy są wygrywające? Jakie jest prawdopodobieństwo, że co najmniej jeden los jest wygrywający?
Ukryj
Podobne zadania
Do worka wrzucono 50 losów loteryjnych w tym 15 wygrywających. Wyciągamy trzy losy z worka. Jakie jest prawdopodobieństwo, że jest wśród nich zarówno los wygrywający jak i przegrywający?
Rzucamy dwiema sześciennymi kostkami.
- Jakie jest prawdopodobieństwo, że suma oczek będzie równa 4?
- Czy bardziej prawdopodobne jest, że suma wyrzuconych oczek będzie równa 5, czy że będzie równa 10?
- Jakie jest najbardziej prawdopodobna suma wyrzuconych oczek?
Oblicz prawdopodobieństwo wylosowania spośród wszystkich liczb trzycyfrowych liczby, której suma cyfr jest równa 2?
Pięć ponumerowanych kul rozmieszczamy losowo w 5 pudełkach. Jakie jest prawdopodobieństwo, że dokładnie dwa pudełka będą puste?
Ukryj
Podobne zadania
Sześć ponumerowanych kul rozmieszczamy losowo w 5 pudełkach. Jakie jest prawdopodobieństwo, że dokładnie dwa pudełka będą puste?
Paulina ma w szafie 20 bluzek w kilku kolorach. W tabelce przedstawiono, jaki procent bluzek stanowią bluzki w danym kolorach
| Kolor bluzki | % |
| czerwony | 15 |
| niebieski | 70 |
| czarny | 5 |
| biały | 10 |
Oblicz prawdopodobieństwo, że wybrana losowo bluzka jest niebieska.
Karol i Antek grają w rzutki. Karol trafia w środek tarczy z prawdopodobieństwem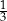 
, a Antek z prawdopodobieństwem 
. Rzucamy symetryczną, sześcienną kostką do gry. Jeżeli wypadnie liczba podzielna przez 3, to Karol dwa razy rzuca do tarczy. W przeciwnym wypadku Antek dwa razy rzuca do tarczy. Oblicz prawdopodobieństwa zdarzenia polegającego na tym, że w żadnym z tych dwóch wykonanych rzutów nie zostanie trafiony środek tarczy.
Jakie jest prawdopodobieństwo tego, że losowo wybrane 4 różne wierzchołki sześcianu są wierzchołkami czworościanu foremnego?
Ukryj
Podobne zadania
Oblicz prawdopodobieństwo tego, że trzy losowo wybrane wierzchołki sześcianu są wierzchołkami trójkąta równobocznego.
- Wpuszczony do labiryntu szczur, dochodząc do rozwidlenia dróg, dwa razy częściej skręca w lewo niż w prawo. Jakie jest prawdopodobieństwo tego, że dotrze do pokarmu (oznaczonego na rysunku
)? 
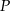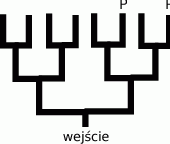
- Inny szczur wpuszczony do tego samego labiryntu, dochodząc do rozwidlenia dróg, skręca w prawo w
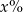przypadków. Oblicz 
, jeśli prawdopodobieństwo tego, że dotrze do pokarmu, jest równe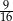 
.
W urnie jest 15 kartek, ponumerowanych liczbami od 1 do 15. Wyciągamy 5 kartek bez zwracania. Jakie jest prawdopodobieństwo, że numer trzeciej kartki jest liczbą podzielną przez 3 i jednocześnie numer piątej kartki jest liczbą podzielną przez 5?
Rzucamy 7 razy dwiema monetami. Oblicz prawdopodobieństwo, że co najmniej 6 razy wyrzucimy dwie reszki.
Oblicz prawdopodobieństwo tego, że losowo wybrana liczba całkowita dodatnia mniejsza od 10000 jest czterocyfrowa.
Z pudełka, w którym jest 15 kul ponumerowanych kolejnymi liczbami od 1 do 15, losujemy bez zwracania 5 kul. Oblicz, jakie jest prawdopodobieństwo, że wśród wylosowanych kul jest dokładnie jedna para kul z sumą numerów równą 16.
Ukryj
Podobne zadania
Z pudełka, w którym jest 13 kul ponumerowanych kolejnymi liczbami od 1 do 13, losujemy bez zwracania 5 kul. Oblicz, jakie jest prawdopodobieństwo, że wśród wylosowanych kul jest dokładnie jedna para kul z sumą numerów równą 14.
Rozważmy zbiór wszystkich czteroelementowych podzbiorów zbioru wierzchołków pewnego prostopadłościanu. Oblicz prawdopodobieństwo wylosowania takiego podzbioru, którego elementy są wierzchołkami prostokąta.
Ze zbioru liczb naturalnych pięciocyfrowych wybieramy losowo jedną liczbę. Oblicz prawdopodobieństwo otrzymania liczby podzielnej przez 15.
Ukryj
Podobne zadania
Ze zbioru liczb naturalnych czterocyfrowych wybieramy losowo jedną liczbę. Oblicz prawdopodobieństwo otrzymania liczby podzielnej przez 11.
Rzucamy dwukrotnie kostką do gry. Jakie jest prawdopodobieństwo, że suma wyrzuconych oczek jest większa niż 9, jeżeli wiadomo, że dokładnie jeden raz wypadło 6 oczek?
Rozważmy rzut sześcioma kostkami do gry, z których każda ma inny kolor. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że uzyskany wynik rzutu spełnia równocześnie trzy warunki:
– dokładnie na dwóch kostkach otrzymano po jednym oczku;
– dokładnie na trzech kostkach otrzymano po sześć oczek;
– suma wszystkich otrzymanych liczb oczek jest parzysta.
Zbiór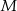 
tworzą wszystkie liczby naturalne dwucyfrowe, w zapisie których występują dwie różne cyfry spośród: 1, 2, 3, 4, 5. Ze zbioru 
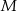losujemy jedną liczbę, przy czym każda liczba z tego zbioru może być wylosowana z tym samym prawdopodobieństwem. Oblicz prawdopodobieństwo, że wylosujemy liczbę większą od 20, w której cyfra dziesiątek jest mniejsza od cyfry jedności.
Wśród 10 tysięcy mieszkańców pewnego miasta przeprowadzono sondaż dotyczący budowy przedszkola publicznego. Wyniki sondażu przedstawiono w tabeli.
| Badane grupy | Liczba osób popierających budowę przedszkola | Liczba osób niepopierających budowy przedszkola |
| Kobiety | 5140 | 1860 |
| Mężczyźni | 2260 | 740 |
Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że losowo wybrana osoba, spośród ankietowanych, popiera budowę przedszkola, jeśli wiadomo, że jest mężczyzną.
Ukryj
Podobne zadania
Wśród 1200 uczniów pewnego liceum przeprowadzono sondaż dotyczący funkcjonowania sklepiku szkolnego. Wyniki sondażu przedstawiono w tabeli.
| Badane grupy | Liczba uczniów zadowolonych z asortymentu sklepiku | Liczba uczniów niezadowolonych z asortymentu sklepiku |
| Chłopcy | 320 | 260 |
| Dziewczęta | 280 | 340 |
Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że losowo wybrana osoba, spośród ankietowanych, jest zadowolona z asortymentu sklepiku, jeśli wiadomo, że jest dziewczynką.
Z talii 52 kart w czterech kolorach wybieramy losowo 2 karty. Oblicz prawdopodobieństwo, że wybrane karty to król i as, przy założeniu, że wybrane karty mają różne kolory.
