Prawdopodobieństwo/Szkoła średnia - zadania z matematyki

/Szkoła średnia/Prawdopodobieństwo

Do windy na parterze budynku wsiadło 6 osób, po czym każda z nich w sposób losowy wysiadła na jednym z trzech pięter budynku. Jakie jest prawdopodobieństwo, że na jednym z pięter wysiadły dokładnie 4 osoby?

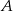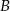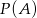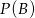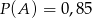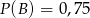Niech , będą zdarzeniami o prawdopodobieństwach P(A ) i P (B ) . Wykaż, że jeżeli P (A) = 0,85 i P(B ) = 0,75 , to prawdopodobieństwo warunkowe spełnia nierówność 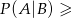P (A |B ) ≥ 0,8.

W klasie IIIA jest 12 dziewcząt i 14 chłopców, natomiast w klasie IIIB jest 10 dziewcząt i 16 chłopców. Rzucamy cztery razy sześcienną kostką do gry. Jeśli suma wyrzuconych oczek jest liczbą parzystą i co najmniej na jednej kostce wypadła parzysta liczba oczek, to wybieramy trzyosobową delegację z klasy IIIA, w przeciwnym wypadku z klasy IIIB. Oblicz prawdopodobieństwo, że w skład delegacji wejdzie co najmniej jeden chłopiec.

Umieszczamy króla szachowego w lewym dolnym rogu 64-polowej szachownicy, a następnie siedem razy przesuwamy go losowo w górę lub w prawo (za każdym razem na nowo losujemy kierunek przesunięcia).

Zakładając, że wylosowanie każdego kierunku jest jednakowo prawdopodobne, oblicz prawdopodobieństwo, że na końcu król nie znajdzie się w rogu szachownicy.

Rzucamy trzy razy kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że w trzecim rzucie otrzymamy dwa razy więcej oczek niż w pierwszym rzucie.

Ukryj Podobne zadania

Rzucamy trzy razy kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że w pierwszym rzucie otrzymamy dwa razy więcej oczek niż w trzecim rzucie.

W pudełku są cztery kartki, na których wypisano liczby 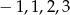− 1,1,2,3 (na każdej kartce jedną liczbę). Losujemy jedną kartkę, zapisujemy liczbę i zwracamy kartkę do pudełka. Następnie losujemy drugą kartkę i zapisujemy liczbę. Wylosowane liczby tworzą parę 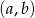(a,b) , gdzie jest liczbą wylosowaną za pierwszym razem, zaś 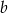liczbą wylosowaną za drugim razem. Oblicz prawdopodobieństwo zdarzenia

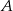– iloczyn wylosowanych liczb jest liczbą pierwszą;
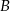– różnica wylosowanych liczb jest liczbą parzystą.

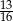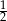W urnie znajdują się drewniane klocki, przy czym każdy z klocków jest biały lub czarny oraz każdy z klocków ma kształt kuli lub sześcianu. Wiadomo, że prawdopodobieństwo wylosowania czarnego klocka jest równe 1316- , prawdopodobieństwo wylosowania klocka w kształcie sześcianu jest równe 5 8 , a prawdopodobieństwo wylosowania klocka, który jest biały lub jest kulą jest równe 1 2 . Oblicz prawdopodobieństwo wybrania klocka, który jest białą kulą.

Z pewnej grupy osób, w której jest dwa razy więcej mężczyzn niż kobiet, wybrano losowo dwuosobową delegację. Prawdopodobieństwo tego, że w delegacji znajdą się tylko kobiety jest równe 0,1. Oblicz, ile kobiet i ilu mężczyzn jest w tej grupie.

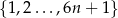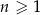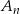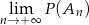Ze zbioru liczb {1,2 ...,6n + 1} , n ≥ 1 losujemy kolejno trzy razy po jednej liczbie bez zwracania. Niech oznacza zdarzenie polegające na tym, że iloczyn wylosowanych liczb jest podzielny przez 6. Oblicz granicę lim P(An ) n→+ ∞ .

Z talii 52 kart losujemy bez zwracania dwie karty. Jakie jest prawdopodobieństwo wylosowania dwóch asów?

Ukryj Podobne zadania

Z talii 52 kart losujemy bez zwracania dwie karty. Jakie jest prawdopodobieństwo wylosowania dwóch kierów?

Z talii 52 kart losujemy bez zwracania dwie karty. Jakie jest prawdopodobieństwo wylosowania asa i króla?

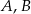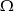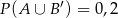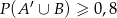Zdarzenia losowe A ,B są zawarte w oraz ′ P (A ∪ B ) = 0 ,2 . Wykaż, że P (A ′ ∪ B) ≥ 0,8 .

W urnie jest 2 razy więcej kul czarnych niż białych i 3 razy więcej kul zielonych niż białych. Przy losowaniu 3 kul z tej urny prawdopodobieństwo wylosowania 3 kul różnych kolorów wynosi 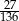21736 . Jakie jest prawdopodobieństwo wylosowania z urny 3 kul, wśród których dokładnie 2 będą tego samego koloru.

Rzucamy dwiema sześciennymi kostkami. Jakie jest prawdopodobieństwo, że na pierwszej kostce wypadło dwa razy mniej oczek niż na drugiej?

Ukryj Podobne zadania

Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo otrzymania iloczynu oczek równego 6.

Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia 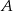polegającego na tym, że liczba oczek w drugim rzucie jest o 1 większa od liczby oczek w pierwszym rzucie.

Rzucamy dwa razy kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że w pierwszym rzucie wypadnie podzielna przez 3 liczba oczek.

Rzucamy dwukrotnie sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma liczb oczek otrzymanych na obu kostkach jest większa od 6 i iloczyn tych liczb jest nieparzysty.

Rzucamy dwiema sześciennymi kostkami. Jakie jest prawdopodobieństwo, że co najmniej na jednej kostce będzie jedynka?

Rzucamy dwiema sześciennymi kostkami. Jakie jest prawdopodobieństwo, że na każdej kostce będzie co najmniej 5 oczek?

Rzucamy dwiema sześciennymi kostkami. Jakie jest prawdopodobieństwo, że suma oczek będzie równa 4?

Rzucamy dwiema sześciennymi kostkami. Jakie jest prawdopodobieństwo, że na obu kostkach będzie ta sama liczba oczek?

Rzucamy czerwoną i zieloną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na wyrzuceniu takiej samej liczby oczek na obu kostkach.

Gracz rzuca dwukrotnie symetryczną sześcienną kostką do gry i oblicza sumę liczb wyrzuconych oczek. Oblicz prawdopodobieństwo zdarzenia 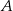polegającego na tym, że suma liczb wyrzuconych oczek jest równa 4 lub 5, lub 6.

Rzucamy dwa razy symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo otrzymania iloczynu oczek równego 5.

Gracz rzuca dwukrotnie symetryczną sześcienną kostką do gry i oblicza wartość bezwzględną różnicy liczb wyrzuconych oczek. Oblicz prawdopodobieństwo zdarzenia 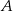polegającego na tym, że obliczona wartość bezwzględna różnicy wyrzuconych oczek jest równa 3, 4 lub 5.

Rzucamy dwa razy kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że w drugim rzucie wypadnie parzysta liczba oczek.

Doświadczenie losowe polega na dziesięciokrotnym rzucie symetryczną monetą. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że w tym doświadczeniu losowym orzeł wypadł dokładnie trzy razy z rzędu, jeśli wiadomo, że wypadł dokładnie trzy razy.

Każdy z trojga chłopców pomyślał sobie liczbę dwucyfrową. Jakie jest prawdopodobieństwo, że żadne dwie z tych osób nie pomyślały tej samej liczby? Wynik podaj w postaci ułamka nieskracalnego.

Z cyfr 0, 1, 2, 3, 4 układamy wszystkie możliwe liczby trzycyfrowe o różnych cyfrach. Ze zbioru takich liczb losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia 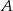– wybrana liczba trzycyfrowa ma tę własność, że cyfry: setek, dziesiątek oraz jedności (w podanej kolejności) tworzą ciąg arytmetyczny.

W pewnej klasie okazało się, że są 3 osoby, które urodziły się w kwietniu tego samego roku i są dwie osoby, które urodziły się w lipcu tego samego roku. Oblicz prawdopodobieństwo, że troje z tych 5 uczniów urodziło się tego samego dnia roku.

W pudełku znajduje się 6 kul czarnych i 4 kule białe. Rzucamy dwa razy monetą. Jeśli otrzymamy 2 orły, losujemy z pudełka kolejno bez zwracania 2 kule. W pozostałych przypadkach losujemy jedną kulę. Oblicz prawdopodobieństwo, że wśród wylosowanych kul jest dokładnie jedna kula czarna.

Ukryj Podobne zadania

W pudełku znajdują się 4 kule czarne i 6 kul białych. Rzucamy dwa razy monetą. Jeśli otrzymamy 2 reszki, losujemy z pudełka kolejno bez zwracania 2 kule. W pozostałych przypadkach losujemy trzy kule. Oblicz prawdopodobieństwo, że wśród wylosowanych kul jest dokładnie jedna kula czarna.

Poniższy diagram przedstawia wyniki ankiety znajomości języków obcych wśród uczniów pewnej szkoły.

Oblicz prawdopodobieństwo, że losowo wybrana osoba z ankietowanych zna

język angielski,
co najmniej jeden język obcy.

Oblicz prawdopodobieństwo tego, że losowo wybrana liczba trzycyfrowa ma cyfrę setek mniejszą od cyfry dziesiątek, a cyfrę jedności równą cyfrze setek.

Strona 10 z 22