W loterii szkolnej losujemy jeden spośród 100 losów, przy czym w przypadku wyciągnięcia losu przegrywającego możemy wylosować jeszcze jeden los. Ile losów w tej loterii jest wygrywających, jeżeli prawdopodobieństwo wygranej jest równe 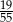 ?
?
/Szkoła średnia/Prawdopodobieństwo
W loterii szkolnej losujemy jeden spośród 100 losów, przy czym w przypadku wyciągnięcia losu przegrywającego możemy wylosować jeszcze jeden los. Ile losów w tej loterii jest przegrywających, jeżeli prawdopodobieństwo wygranej jest równe 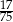 ?
?
W jednej szufladzie znajduje się 6 czapek: 3 zielone, 2 czerwone i 1 niebieska, a w drugiej szufladzie jest 7 szalików: 2 zielone, 1 czerwony i 4 niebieskie. Wyjęto losowo jedną czapkę i jeden szalik. Oblicz prawdopodobieństwo zdarzenia A – wylosowana czapka i wylosowany szalik są tego samego koloru.
W kuchni stoją dwa koszyki. W pierwszym jest 9 papryk: 1 zielona, 4 czerwone i 4 żółte. W drugim 12 papryk: 4 zielone, 3 czerwone i 5 żółtych. Kucharz wyjmuje losowo po jednej papryce z każdego koszyka. Oblicz prawdopodobieństwo, że obie papryki będą tego samego koloru.
Ze zbioru 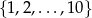 losujemy kolejno 3 liczby (mogą się powtarzać). Wyznacz prawdopodobieństwo wyboru takiej trójki
losujemy kolejno 3 liczby (mogą się powtarzać). Wyznacz prawdopodobieństwo wyboru takiej trójki 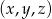 liczb, dla której
liczb, dla której 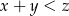 .
.
Ze zbioru cyfr 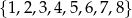 losujemy kolejno dwie cyfry (losowanie bez zwracania) i tworzymy liczby dwucyfrowe tak, że pierwsza wylosowana cyfra jest cyfrą dziesiątek, a druga – cyfrą jedności. Oblicz prawdopodobieństwo utworzenia liczby podzielnej przez 4.
losujemy kolejno dwie cyfry (losowanie bez zwracania) i tworzymy liczby dwucyfrowe tak, że pierwsza wylosowana cyfra jest cyfrą dziesiątek, a druga – cyfrą jedności. Oblicz prawdopodobieństwo utworzenia liczby podzielnej przez 4.
Ze zbioru ośmiu kolejnych liczb naturalnych – od 1 do 8 – losujemy kolejno bez zwracania dwa razy po jednej liczbie. Niech 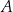 oznacza zdarzenie polegające na tym, że suma wylosowanych liczb jest dzielnikiem liczby 12. Oblicz prawdopodobieństwo zdarzenia
oznacza zdarzenie polegające na tym, że suma wylosowanych liczb jest dzielnikiem liczby 12. Oblicz prawdopodobieństwo zdarzenia 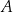 .
.
Mamy dwa pudełka: w pierwszym znajduje się 6 kul ponumerowanych kolejnymi liczbami od 1 do 6, a w drugim – 7 kul ponumerowanych kolejnymi liczbami od 2 do 8. Losujemy po jednej kuli z każdego pudełka i tworzymy liczbę dwucyfrową w ten sposób, że numer kuli wylosowanej z pierwszego pudełka jest cyfrą dziesiątek, a numer kuli wylosowanej z drugiego – cyfrą jedności tej liczby. Oblicz prawdopodobieństwo, że utworzona liczba jest podzielna przez 9.
Ze zbioru ośmiu kolejnych liczb naturalnych – od 1 do 8 – losujemy kolejno bez zwracania dwa razy po jednej liczbie. Niech 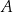 oznacza zdarzenie polegające na tym, że suma wylosowanych liczb jest dzielnikiem liczby 8. Oblicz prawdopodobieństwo zdarzenia
oznacza zdarzenie polegające na tym, że suma wylosowanych liczb jest dzielnikiem liczby 8. Oblicz prawdopodobieństwo zdarzenia 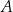 .
.
Mamy dwa pudełka: w pierwszym znajduje się 6 kul ponumerowanych kolejnymi liczbami od 1 do 6, a w drugim – 8 kul ponumerowanych kolejnymi liczbami od 1 do 8. Losujemy po jednej kuli z każdego pudełka i tworzymy liczbę dwucyfrową w ten sposób, że numer kuli wylosowanej z pierwszego pudełka jest cyfrą dziesiątek, a numer kuli wylosowanej z drugiego – cyfrą jedności tej liczby. Oblicz prawdopodobieństwo, że utworzona liczba jest podzielna przez 11.
Ze zbioru wszystkich liczb naturalnych dwucyfrowych, których cyfra dziesiątek należy do zbioru 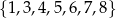 , a cyfra jedności należy do zbioru
, a cyfra jedności należy do zbioru 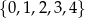 , losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy liczbę dwucyfrową, która jest podzielna przez 8.
, losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy liczbę dwucyfrową, która jest podzielna przez 8.
Ze zbioru wszystkich liczb naturalnych dwucyfrowych, których cyfra dziesiątek należy do zbioru 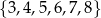 , a cyfra jedności należy do zbioru
, a cyfra jedności należy do zbioru 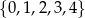 , losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy liczbę dwucyfrową, która jest podzielna przez 4.
, losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy liczbę dwucyfrową, która jest podzielna przez 4.
W dwóch pojemnikach znajdują się ponumerowane kule. W pierwszym pojemniku są kule z numerami: 1, 2, 3, 4, 5, w drugim z numerami: 4, 5, 6, 7, 8, 9. Losujemy po jednej kuli z każdego pojemnika i tworzymy liczbę dwucyfrową. Numer kuli wylosowanej z pierwszego pojemnika jest cyfrą dziesiątek, numer kuli wylosowanej z drugiego pojemnika jest cyfrą jedności. Oblicz prawdopodobieństwo zdarzenia, że utworzona liczba jest podzielna przez 4.
Spośród liczb naturalnych sześciocyfrowych wybieramy jedną liczbę. Jakie jest prawdopodobieństwo wybrania liczby, której iloczyn cyfr jest podzielny przez 9, jeżeli wiadomo, że każda cyfra wylosowanej liczby jest większa od 1?
Do koszyka włożono 12 jabłek, w tym dwa jabłka lobo. Po kilku dniach przechowywania z koszyka usunięto dwa popsute jabłka. Następnie losowo wybrano jedno jabłko. Oblicz prawdopodobieństwo, że wybrano jabłko lobo. Wynik podaj w postaci ułamka nieskracalnego.
Ze zbioru 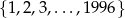 losujemy jedną liczbę. Oblicz prawdopodobieństwo, że wylosowana liczba jest podzielna przez:
losujemy jedną liczbę. Oblicz prawdopodobieństwo, że wylosowana liczba jest podzielna przez:
- 6
- 4 lub 6
- 4 lub 6 lub 10
Oblicz prawdopodobieństwo tego, że w trzech rzutach symetryczną sześcienną kostką do gry suma kwadratów liczb uzyskanych oczek będzie podzielna przez 3.
Oblicz prawdopodobieństwo tego, że w trzech rzutach symetryczną sześcienną kostką do gry suma kwadratów liczb uzyskanych oczek będzie podzielna przez 5.
Oblicz prawdopodobieństwo tego, że w trzech rzutach symetryczną sześcienną kostką do gry suma kwadratów liczb uzyskanych oczek będzie podzielna przez 4.
W pewnym wagonie kolejowym pasażerowie siadają w sposób losowy na 54 siedzeniach, które są ustawione po trzy siedzenia w jednym rzędzie. Do wagonu wsiadło o 3 pasażerów mniej niż dostępna liczba siedzeń i dokładnie troje z tych pasażerów to mężczyźni. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że mężczyźni usiedli w jednym rzędzie i jednocześnie jeden cały rząd pozostał pusty.
Grupę 12 uczniów, wśród których jest 6 dziewczynek i 6 chłopców podzielono na 3 równoliczne grupy. Oblicz prawdopodobieństwo tego, że w każdej z utworzonych grup będzie tyle samo dziewcząt.
Doświadczenie losowe polega na tym, że losujemy jednocześnie dwie liczby ze zbioru
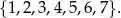
Oblicz prawdopodobieństwo warunkowe, że wśród wylosowanych liczb jest liczba 6, pod warunkiem, że suma wylosowanych liczb jest parzysta.
Zdarzenia losowe 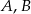 są zawarte w
są zawarte w 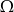 oraz
oraz 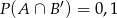 i
i 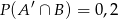 . Wykaż, że
. Wykaż, że 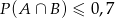 (
(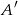 oznacza zdarzenie przeciwne do zdarzenia
oznacza zdarzenie przeciwne do zdarzenia 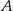 ,
, 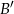 oznacza zdarzenie przeciwne do zdarzenia
oznacza zdarzenie przeciwne do zdarzenia 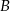 ).
).
Ze zbioru wszystkich liczb trzycyfrowych, które są podzielne przez 7 wybieramy losowo 5 różnych liczb. Oblicz prawdopodobieństwo tego, że jedną z tych liczb jest 546, a wśród pozostałych 4 liczb jest dokładnie jedna liczba mniejsza od 546. Wynik podaj w postaci ułamka nieskracalnego.
W fabryce obuwia pracuje pięć linii produkcyjnych produkujących ten sam model butów. W poniższej tabeli zawarto informacje o wydajności tych linii oraz o odsetku wadliwych par obuwia produkowanych przez każdą z nich.
| Linia produkcyjna | Wydajność | Odsetek wadliwych par |
| I | 60 par/godzinę | 2% |
| II | 50 par/godzinę | 3% |
| III | 40 par/godzinę | 1% |
| IV | 80 par/godzinę | 3% |
| V | 70 par/godzinę | 2% |
Wybieramy losowo jedną parę obuwia wyprodukowaną przez te linie produkcyjne. Jakie jest prawdopodobieństwo, że wybrana para nie okaże się wadliwa?
Sześcian pomalowano, a następnie rozcięto na 1000 jednakowych sześcianików, które wrzucono do pudełka i wymieszano. Oblicz prawdopodobieństwo wylosowania z tego pudełka jednego, który:
- będzie miał dwie ściany pomalowane;
- będzie miał trzy ściany pomalowane;
- będzie miał jedną lub dwie ściany pomalowane.
W urnie jest 7 kul czarnych i 3 białe. Losujemy z tej urny pięć razy po jednej kuli i po każdym losowaniu wkładamy wylosowaną kulę z powrotem do urny oraz dokładamy do urny dwie kule w kolorze wylosowanej kuli. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że dokładnie dwa razy wylosujemy kulę białą.
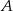 i
i 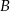 są takim zdarzeniami losowymi zawartymi w
są takim zdarzeniami losowymi zawartymi w 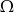 , że
, że 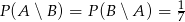 i
i 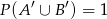 . Oblicz
. Oblicz 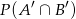 .
.
Oblicz prawdopodobieństwo 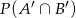 , jeśli
, jeśli 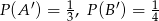 i
i 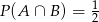 .
.
Oblicz prawdopodobieństwo 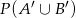 , jeśli
, jeśli 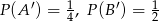 i
i 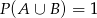 .
.
W urnie znajdują się kule czarne, białe i niebieskie, przy czym są co najmniej dwie kule każdego koloru i w sumie jest 15 kul. Losujemy z urny trzy kule. Rozważmy następujące zdarzenia 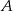 – wylosowano trzy kule tego samego koloru;
– wylosowano trzy kule tego samego koloru;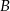 – żadne dwie z wylosowanych kul nie są tego samego koloru.
– żadne dwie z wylosowanych kul nie są tego samego koloru.
Oblicz prawdopodobieństwo zdarzenia 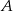 jeżeli prawdopodobieństwo zdarzenia
jeżeli prawdopodobieństwo zdarzenia 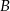 jest równe
jest równe 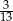 .
.
Rzucono 3 razy monetą i określono zdarzenia: 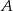 – wypadły dokładnie dwa orły,
– wypadły dokładnie dwa orły, 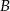 – wypadł orzeł za pierwszym razem. Oblicz prawdopodobieństwo zdarzenia
– wypadł orzeł za pierwszym razem. Oblicz prawdopodobieństwo zdarzenia 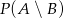 .
.

