Ze zbioru siedmiu liczb naturalnych 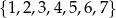 losujemy dwie różne liczby. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że większą z wylosowanych liczb będzie liczba 5.
losujemy dwie różne liczby. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że większą z wylosowanych liczb będzie liczba 5.
/Szkoła średnia/Prawdopodobieństwo
Ze zbioru ośmiu liczb naturalnych 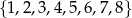 losujemy dwie różne liczby. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że mniejszą z wylosowanych liczb będzie liczba 3.
losujemy dwie różne liczby. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że mniejszą z wylosowanych liczb będzie liczba 3.
W pierwszej urnie są kule czarne i białe, w drugiej 10 kul niebieskich i 15 kul zielonych, a w trzeciej – 14 kul niebieskich i 7 zielonych. Najpierw losujemy kulę z pierwszej urny, a następnie losujemy kulę z drugiej albo z trzeciej urny w zależności od tego, czy z pierwszej urny wylosowaliśmy odpowiednio kulę białą, czy czarną. Oblicz prawdopodobieństwo wylosowania czarnej kuli z pierwszej urny, jeżeli prawdopodobieństwo wylosowania według opisanego schematu kuli niebieskiej jest takie samo jak zielonej.
Rzucamy dwa razy kostką do gry. Jeśli suma oczek wyrzuconych na obu kostkach jest liczbą podzielną przez 3, losujemy jedną liczbę ze zbioru 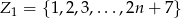 , w przeciwnym przypadku losujemy jedną liczbę ze zbioru
, w przeciwnym przypadku losujemy jedną liczbę ze zbioru 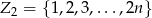 . Oblicz prawdopodobieństwo wylosowania liczby parzystej.
. Oblicz prawdopodobieństwo wylosowania liczby parzystej.
Ze zbioru wszystkich liczb naturalnych czterocyfrowych losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba jest podzielna przez 4 lub 9, jeśli wiadomo, że jest ona podzielna przez 6.
Uczniowie pewnej szkoły zostali zabrani na wycieczkę do muzeum. W wycieczce wzięło udział 11 uczniów klasy pierwszej, 30 uczniów klasy drugiej i 9 uczniów klasy trzeciej. Przed wejściem do muzeum uczniowie zostali ustawieni w kolejce jeden za drugim. Oblicz prawdopodobieństwo tego, że pierwsi trzej uczniowie w tej kolejce to uczniowie drugiej klasy.
Rzucamy trzykrotnie symetryczną kostką sześcienną do gry. Oblicz prawdopodobieństwa następujących zdarzeń:
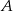 – na każdej kostce wypadnie nieparzysta liczba oczek,
– na każdej kostce wypadnie nieparzysta liczba oczek, 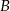 – suma kwadratów liczb wyrzuconych oczek będzie podzielna przez 3.
– suma kwadratów liczb wyrzuconych oczek będzie podzielna przez 3.
Dwóch strzelców strzela do celu. Jeden trafia z prawdopodobieństwem 0,6, a drugi trafia z prawdopodobieństwem 0,8. Oblicz prawdopodobieństwo, że jeśli wykonają po jednym strzale, to cel zostanie trafiony dokładnie 1 raz.
Wykaż, że jeśli 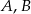 są dowolnymi zdarzeniami przestrzeni
są dowolnymi zdarzeniami przestrzeni 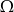 , to
, to  .
.
W pierwszej urnie znajduje się 5 kul białych i 17 kul czarnych. W drugiej urnie znajduje się 16 kul białych i 34 kule czarne. Ile kul białych należy przełożyć z drugiej urny do pierwszej, aby wylosowanie kuli białej z obu urn było jednakowo prawdopodobne?
W pierwszej urnie znajdują się 4 kule białe i 13 kul czarnych. W drugiej urnie znajduje się 17 kul białych i 26 kul czarnych. Ile kul białych należy przełożyć z drugiej urny do pierwszej, aby wylosowanie kuli białej z obu urn było jednakowo prawdopodobne?
Z pojemnika, w którym znajduje się pięć kul: dwie białe i trzy czerwone, losujemy dwa razy po jednej kuli bez zwracania. Oblicz prawdopodobieństwo, że wylosujemy co najmniej jedną kulę białą. Wynik przedstaw w postaci ułamka nieskracalnego.
Z pojemnika, w którym znajduje się pięć kul: dwie białe i trzy czerwone, losujemy dwa razy po jednej kuli bez zwracania. Oblicz prawdopodobieństwo, że wylosujemy co najmniej jedną kulę czerwoną. Wynik przedstaw w postaci ułamka nieskracalnego.
W urnie znajduje się 5 kul białych, 3 kule czerwone i 1 zielona. Losujemy 1 kulę. Oblicz prawdopodobieństwo wylosowania kuli białej.
W urnie znajduje się 5 kul białych, 3 kule czerwone i 1 zielona. Losujemy 1 kulę. Oblicz prawdopodobieństwo wylosowania kuli białej lub czerwonej.
- Na ile sposobów można ze standardowej talii 52 kart wybrać 13 kart tak, aby mieć co najwyżej jednego czerwonego (kier lub karo) asa?
- Jakie jest prawdopodobieństwo takiego zdarzenia?
Ze zbioru liczb  wybieramy losowo jednocześnie cztery liczby. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że najmniejszą wylosowaną liczbą będzie 3 lub największą wylosowaną liczbą będzie 7.
wybieramy losowo jednocześnie cztery liczby. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że najmniejszą wylosowaną liczbą będzie 3 lub największą wylosowaną liczbą będzie 7.
Wśród 150 mieszkańców pewnego osiedla przeprowadzono ankietę. Zadano pytanie, z jakiej sieci telefonii komórkowej korzystają. Wyniki badania przedstawiono w tabeli:
| Sieć | Ile osób korzysta |
| „Krzyżyk” | 75 |
| „Kółko” | 60 |
Okazało się, że wśród ankietowanych, 10 osób posiada telefony w obydwu sieciach. Oblicz prawdopodobieństwo, że losowo wybrana osoba spośród ankietowanych nie posiada telefonu w żadnej z wymienionych sieci. Wynik przedstaw w formie nieskracalnego ułamka.
Niech  i
i  . Oblicz prawdopodobieństwo, że zbiór wartości losowo utworzonej funkcji
. Oblicz prawdopodobieństwo, że zbiór wartości losowo utworzonej funkcji 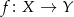 jest dwuelementowy.
jest dwuelementowy.
Losujemy dwie różne liczby całkowite  i
i 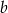 z przedziału
z przedziału 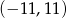 . Oblicz prawdopodobieństwo zdarzenia
. Oblicz prawdopodobieństwo zdarzenia 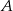 – równanie
– równanie 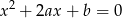 nie ma rozwiązań.
nie ma rozwiązań.
Z ustalonego zbioru  liczb rzeczywistych losujemy kolejno
liczb rzeczywistych losujemy kolejno 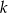 liczb, otrzymując ciąg różnowartościowy
liczb, otrzymując ciąg różnowartościowy 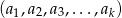 . Zakładając, że
. Zakładając, że 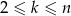 , oblicz prawdopodobieństwo, że ten ciąg nie jest ciągiem rosnącym.
, oblicz prawdopodobieństwo, że ten ciąg nie jest ciągiem rosnącym.
Każda ściana dwudziestościanu foremnego 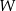 jest trójkątem równobocznym, a z każdego wierzchołka tej bryły wychodzi 5 krawędzi. Wybieramy losowo dwa różne wierzchołki wielościanu
jest trójkątem równobocznym, a z każdego wierzchołka tej bryły wychodzi 5 krawędzi. Wybieramy losowo dwa różne wierzchołki wielościanu 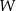 . Jakie jest prawdopodobieństwo tego, że odcinek łączący te dwa wierzchołki nie jest krawędzią wielościanu
. Jakie jest prawdopodobieństwo tego, że odcinek łączący te dwa wierzchołki nie jest krawędzią wielościanu 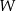 ?
?
Rzucamy trzy razy symetryczną sześcienną kostką do gry. Opisz zbiór wszystkich zdarzeń elementarnych, a następnie oblicz prawdopodobieństwo, że w każdym rzucie liczba oczek będzie większa od numeru rzutu.
Z cyfr 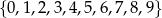 losujemy 3 cyfry i zapisujemy z ich pomocą liczbę 3-cyfrową o niepowtarzających się cyfrach, przy czym zakładamy, że pierwsza cyfra jest niezerowa. Oblicz prawdopodobieństwo otrzymania liczby nieparzystej.
losujemy 3 cyfry i zapisujemy z ich pomocą liczbę 3-cyfrową o niepowtarzających się cyfrach, przy czym zakładamy, że pierwsza cyfra jest niezerowa. Oblicz prawdopodobieństwo otrzymania liczby nieparzystej.
Z cyfr 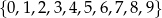 losujemy 3 cyfry i zapisujemy z ich pomocą liczbę 3-cyfrową o niepowtarzających się cyfrach, przy czym zakładamy, że pierwsza cyfra jest niezerowa. Oblicz prawdopodobieństwo otrzymania liczby podzielnej przez 5.
losujemy 3 cyfry i zapisujemy z ich pomocą liczbę 3-cyfrową o niepowtarzających się cyfrach, przy czym zakładamy, że pierwsza cyfra jest niezerowa. Oblicz prawdopodobieństwo otrzymania liczby podzielnej przez 5.
Z cyfr 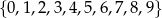 losujemy 3 cyfry i zapisujemy z ich pomocą liczbę 3-cyfrową o niepowtarzających się cyfrach, przy czym zakładamy, że pierwsza cyfra jest niezerowa. Oblicz prawdopodobieństwo otrzymania liczby większej od 666.
losujemy 3 cyfry i zapisujemy z ich pomocą liczbę 3-cyfrową o niepowtarzających się cyfrach, przy czym zakładamy, że pierwsza cyfra jest niezerowa. Oblicz prawdopodobieństwo otrzymania liczby większej od 666.

