Oblicz prawdopodobieństwo tego, że dwa losowo wybrane wierzchołki sześciokąta foremnego o boku długości 1, są końcami odcinka o długości 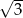 .
.
/Szkoła średnia/Prawdopodobieństwo
Dwa zakłady pracy produkują takie same akumulatory, przy czym stosunek liczby akumulatorów produkowanych dziennie przez pierwszy zakład do liczby akumulatorów produkowanych dziennie przez drugi zakład jest równy  . Badania wykazały, że niektóre z wyprodukowanych akumulatorów mają podwyższoną pojemność, przy czym własność tą ma 40% akumulatorów pochodzących z pierwszego zakładu i 30% akumulatorów pochodzących z drugiego zakładu. Oblicz jakie jest prawdopodobieństwo, że losowo wybrany akumulator pochodzący z dziennej produkcji obu zakładów nie ma podwyższonej pojemności.
. Badania wykazały, że niektóre z wyprodukowanych akumulatorów mają podwyższoną pojemność, przy czym własność tą ma 40% akumulatorów pochodzących z pierwszego zakładu i 30% akumulatorów pochodzących z drugiego zakładu. Oblicz jakie jest prawdopodobieństwo, że losowo wybrany akumulator pochodzący z dziennej produkcji obu zakładów nie ma podwyższonej pojemności.
Ze zbioru liczb 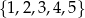 losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia
losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 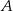 polegającego na wylosowaniu liczb, których iloczyn jest liczbą nieparzystą.
polegającego na wylosowaniu liczb, których iloczyn jest liczbą nieparzystą.
Ze zbioru liczb 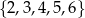 losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia
losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 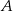 polegającego na wylosowaniu liczb, których iloczyn jest liczbą nieparzystą.
polegającego na wylosowaniu liczb, których iloczyn jest liczbą nieparzystą.
Ze zbioru liczb 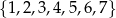 losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia
losujemy dwa razy po jednej liczbie ze zwracaniem. Oblicz prawdopodobieństwo zdarzenia 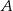 polegającego na wylosowaniu liczb, których iloczyn jest liczbą parzystą.
polegającego na wylosowaniu liczb, których iloczyn jest liczbą parzystą.
Ze zbioru 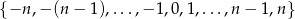 , gdzie
, gdzie 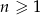 losujemy dwie liczby (mogą się powtarzać). Oblicz jakie jest prawdopodobieństwo, że suma wartości bezwzględnych wylosowanych liczb jest nie większa niż
losujemy dwie liczby (mogą się powtarzać). Oblicz jakie jest prawdopodobieństwo, że suma wartości bezwzględnych wylosowanych liczb jest nie większa niż  .
.
W pudełku umieszczono  kul (
kul (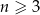 ) wśród których dokładnie 2 kule są czarne, a pozostałe kule są białe. Z tego pudełka losujemy jedną kulę i odkładamy ją na bok. Jeżeli wylosowana kula jest biała, to do pudełka wrzucamy kulę czarną, a gdy wylosowana kula jest czarna, to do pudełka wrzucamy kulę białą. Po przeprowadzonej w ten sposób zmianie zawartości prawdopodobieństwo wylosowania kuli białej z tego pudełka jest równe
) wśród których dokładnie 2 kule są czarne, a pozostałe kule są białe. Z tego pudełka losujemy jedną kulę i odkładamy ją na bok. Jeżeli wylosowana kula jest biała, to do pudełka wrzucamy kulę czarną, a gdy wylosowana kula jest czarna, to do pudełka wrzucamy kulę białą. Po przeprowadzonej w ten sposób zmianie zawartości prawdopodobieństwo wylosowania kuli białej z tego pudełka jest równe 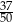 . Oblicz
. Oblicz  .
.
Wiadomo, że 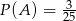 ,
, 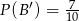 ,
, 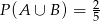 . Oblicz
. Oblicz 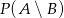 i
i 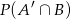 .
.
Dane są dwie urny z kulami. W każdej z urn jest siedem kul. W pierwszej urnie są trzy kule czarne i cztery kule białe, w drugiej urnie są dwie kule czarne i pięć białych. Rzucamy jeden raz symetryczną monetą. Jeżeli wypadnie reszka, to losujemy jedną kulę z pierwszej urny, w przeciwnym przypadku – jedną kulę z drugiej urny. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że w tym doświadczeniu wylosujemy kulę białą.
Ze zbioru liczb naturalnych dwucyfrowych wybieramy losowo jedną liczbę. Oblicz prawdopodobieństwo otrzymania liczby podzielnej przez 15.
Ze zbioru wszystkich liczb naturalnych dwucyfrowych losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia, że wylosujemy liczbę, która jest równocześnie większa od 40 i podzielna przez 3. Wynik zapisz w postaci ułamka zwykłego nieskracalnego.
Ze zbioru wszystkich liczb naturalnych dwucyfrowych losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia, że wylosujemy liczbę, która jest równocześnie mniejsza od 40 i podzielna przez 3. Wynik zapisz w postaci ułamka zwykłego nieskracalnego.
Ze zbioru wszystkich liczb naturalnych dwucyfrowych większych od 53 losujemy jedną liczbę. Niech 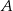 oznacza zdarzenie polegające na wylosowaniu liczby podzielnej przez 7. Oblicz prawdopodobieństwo zdarzenia
oznacza zdarzenie polegające na wylosowaniu liczby podzielnej przez 7. Oblicz prawdopodobieństwo zdarzenia 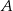 .
.
Oblicz prawdopodobieństwo otrzymania dokładnie dwóch jedynek lub trzech szóstek w doświadczeniu losowym, polegającym na pięciokrotnym rzucie symetryczną sześcienną kostką do gry.
Do kina wybrało się 7 osób, wśród nich Basia i Janek. Wszyscy usiedli w jednym rzędzie, w którym jest dokładnie 7 wolnych miejsc. Oblicz, na ile sposobów wymienione osoby mogą zająć miejsca tak, by Basia i Janek siedzieli obok siebie. Oblicz też prawdopodobieństwo tego, że przy losowym zajmowaniu miejsc Basia i Janek nie siedzą obok siebie.
Oblicz prawdopodobieństwo tego, że przy czterokrotnym rzucie kostką, 3 kolejne wyniki utworzą ciąg geometryczny.
W pojemniku znajdują się dwie kule białe i trzy czerwone. Losujemy dwa razy po jednej kuli bez zwracania. Oblicz prawdopodobieństwo, że wylosujemy co najmniej jedną kulę czerwoną. Wynik przedstaw w postaci ułamka nieskracalnego.
W pojemniku znajdują się dwie kule czerwone i trzy białe. Losujemy dwa razy po jednej kuli bez zwracania. Oblicz prawdopodobieństwo, że wylosujemy co najmniej jedną kulę czerwoną. Wynik przedstaw w postaci ułamka nieskracalnego.
W urnie znajdują się kule białe, zielone i czerwone. Kul zielonych jest dwa razy więcej niż kul białych, a kul czerwonych jest 3 razy więcej niż białych. Wyjęto dwa razy po jednej kuli bez zwracania. Oblicz liczbę kul białych w urnie, jeśli prawdopodobieństwo wylosowania dwóch kul zielonych jest równe 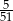 .
.
Każda z urn oznaczonych liczbami 1, 2, 3 zawiera po 3 kule czarne i 4 białe, a każda urna oznaczona liczbami 4, 5, 6 zawiera po 3 czarne i 2 białe kule. Rzucamy sześcienną kostką do gry, a następnie z urny o numerze równym liczbie wyrzuconych oczek losujemy bez zwracania 2 kule. Co jest bardziej prawdopodobne: wylosowanie dwóch kul czarnych, czy dwóch kul białych?
Na trzy półki kładziemy losowo 5 książek. Jakie jest prawdopodobieństwo tego, że jedna (i tylko jedna) z półek zostanie pusta?.
Rzucamy czterokrotnie symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że otrzymamy dokładnie dwie dwójki lub dokładnie dwie piątki. Wynik zapisz w postaci ułamka zwykłego nieskracalnego.
Badania statystyczne pokazały, że średnio 13,9% zapałek jest wadliwych. Jakie jest prawdopodobieństwo, że w pudełku z 90 zapałkami są więcej niż 2 wadliwe?
Ze zbioru liczb 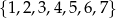 losujemy trzy razy po jednej liczbie bez zwracania. Oblicz prawdopodobieństwo zdarzenia
losujemy trzy razy po jednej liczbie bez zwracania. Oblicz prawdopodobieństwo zdarzenia 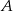 , polegającego na wylosowaniu liczb, których iloczyn jest podzielny przez 4.
, polegającego na wylosowaniu liczb, których iloczyn jest podzielny przez 4.
20 drużyn rozdziela się losowo na 2 grupy po 10 drużyn. Oblicz prawdopodobieństwo tego, że 2 ustalone drużyny znajdą się w różnych grupach.
Dziesięć osób rozdzielono na dwie drużyny po 5 osób. Oblicz prawdopodobieństwo, że osoby 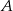 i
i 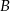 będą w przeciwnych drużynach.
będą w przeciwnych drużynach.
Ze zbioru liczb całkowitych spełniających nierówność 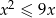 losujemy dwie różne liczby. Wylosowanie każdej liczby z tego zbioru jest jednakowo prawdopodobne. Oblicz prawdopodobieństwo wylosowania dwóch liczb pierwszych.
losujemy dwie różne liczby. Wylosowanie każdej liczby z tego zbioru jest jednakowo prawdopodobne. Oblicz prawdopodobieństwo wylosowania dwóch liczb pierwszych.

