Kąt ostry równoległoboku ma miarę 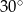 . Odległości punktu przecięcia przekątnych równoległoboku od prostych zawierających jego boki są równe 2 oraz 6 odpowiednio. Oblicz pole równoległoboku i długość jego krótszej przekątnej.
. Odległości punktu przecięcia przekątnych równoległoboku od prostych zawierających jego boki są równe 2 oraz 6 odpowiednio. Oblicz pole równoległoboku i długość jego krótszej przekątnej.
/Szkoła średnia/Geometria/Planimetria/Czworokąt/Równoległobok
Obwód równoległoboku 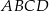 jest równy 26, miara jego kąta rozwartego
jest równy 26, miara jego kąta rozwartego 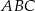 jest równa
jest równa 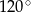 , a promień okręgu wpisanego w trójkąt
, a promień okręgu wpisanego w trójkąt 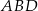 jest równy
jest równy 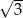 . Oblicz długości boków równoległoboku
. Oblicz długości boków równoległoboku 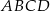 .
.
Wysokości równoległoboku mają długości 2 i 4. Oblicz pole równoległoboku wiedząc, że jego obwód wynosi 30.
Wysokości równoległoboku o obwodzie 20 cm mają długości 2 cm i 3 cm. Oblicz pole równoległoboku.
Wysokości równoległoboku o obwodzie 18 cm mają długości 2 cm i 4 cm. Oblicz pole równoległoboku.
Pole równoległoboku jest równe 24. Stosunek jego wysokości jest równy 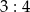 . Długości boków wyrażają się liczbami naturalnymi, a długość każdej z wysokości jest mniejsza od 5 i większa od 2. Oblicz długości boków równoległoboku.
. Długości boków wyrażają się liczbami naturalnymi, a długość każdej z wysokości jest mniejsza od 5 i większa od 2. Oblicz długości boków równoległoboku.
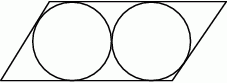
W równoległoboku wpisano dwa przystające okręgi styczne zewnętrznie do siebie (patrz rysunek). Wykaż, że średnica każdego z tych okręgów jest równa różnicy długości dłuższego i krótszego boku tego równoległoboku.
Punkt 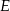 jest środkiem boku
jest środkiem boku 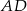 równoległoboku
równoległoboku 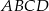 . Pole trójkąta
. Pole trójkąta 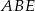 jest równe 2. Oblicz pole równoległoboku.
jest równe 2. Oblicz pole równoległoboku.
Oblicz pole równoległoboku o bokach 7 cm i 12 cm, w którym dwa sąsiednie kąty różnią się o 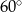 .
.
Punkty 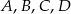 są kolejnymi wierzchołkami równoległoboku o obwodzie równym 26. Wiedząc, że kąt przy wierzchołku
są kolejnymi wierzchołkami równoległoboku o obwodzie równym 26. Wiedząc, że kąt przy wierzchołku 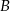 ma miarę
ma miarę 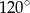 i promień okręgu wpisanego w trójkąt
i promień okręgu wpisanego w trójkąt 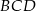 jest równy
jest równy 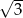 , oblicz długości boków i pole tego równoległoboku.
, oblicz długości boków i pole tego równoległoboku.
Boki równoległoboku mają długości 6 i 14, a jego krótsza przekątna ma długość 11. Oblicz cosinus kąta rozwartego tego równoległoboku.
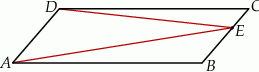
Na rysunku przedstawiono równoległobok 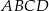 i trójkąt
i trójkąt 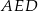 . Punkt
. Punkt 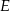 leży na odcinku
leży na odcinku 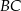 . Uzasadnij, że pole równoległoboku
. Uzasadnij, że pole równoległoboku 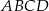 jest dwa razy większe od pola trójkąta
jest dwa razy większe od pola trójkąta 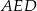 .
.
W równoległoboku o obwodzie równym 144, wysokości 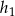 i
i 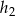 spełniają warunek
spełniają warunek 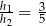 . Oblicz długości boków tego równoległoboku.
. Oblicz długości boków tego równoległoboku.
W równoległoboku o obwodzie równym 96 cm stosunek wysokości jest równy 5:7. Oblicz długości boków tego równoległoboku.
Kąt ostry równoległoboku ma miarę 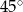 . Punkt wspólny przekątnych równoległoboku jest oddalony od boków o
. Punkt wspólny przekątnych równoległoboku jest oddalony od boków o 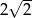 i 2. Oblicz pole równoległoboku oraz długości jego przekątnych.
i 2. Oblicz pole równoległoboku oraz długości jego przekątnych.
Kąt ostry równoległoboku ma miarę 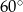 . Stosunek kwadratów długości przekątnych jest równy
. Stosunek kwadratów długości przekątnych jest równy 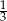 . Wykaż, że ten równoległobok jest rombem.
. Wykaż, że ten równoległobok jest rombem.
- Uzasadnij, że
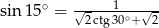
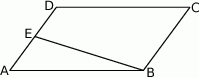
- W równoległoboku
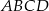 dane są miary kątów
dane są miary kątów 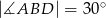 i
i 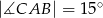 . Oblicz miarę kąta
. Oblicz miarę kąta 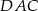 .
.
Dany jest równoległobok 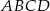 . Na przedłużeniu przekątnej
. Na przedłużeniu przekątnej 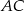 wybrano punkt
wybrano punkt 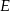 tak, że
tak, że 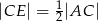 (zobacz rysunek). Uzasadnij, że pole równoległoboku
(zobacz rysunek). Uzasadnij, że pole równoległoboku 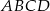 jest cztery razy większe od pola trójkąta
jest cztery razy większe od pola trójkąta 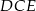 .
.
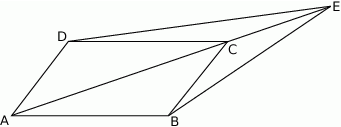
Na przekątnej 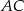 równoległoboku
równoległoboku 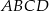 wybrano punkt
wybrano punkt 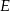 (zobacz rysunek). Uzasadnij, że trójkąty
(zobacz rysunek). Uzasadnij, że trójkąty 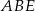 i
i 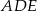 mają równe pola.
mają równe pola.
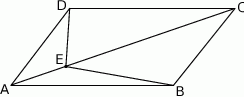
W równoległoboku 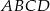 środek
środek 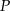 boku
boku 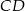 połączono odcinkami z wierzchołkami
połączono odcinkami z wierzchołkami 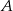 i
i 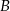 . Wiadomo, że
. Wiadomo, że 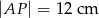 i
i 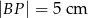 oraz
oraz 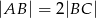 . Oblicz obwód równoległoboku.
. Oblicz obwód równoległoboku.
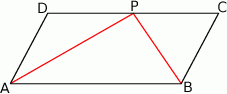
Przekątna równoległoboku, poprowadzona z wierzchołka kąta rozwartego, ma długość 18 cm i dzieli ten kąta na kąty o miarach 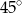 i
i 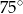 . Oblicz pole równoległoboku. Wynik przedstaw w postaci
. Oblicz pole równoległoboku. Wynik przedstaw w postaci 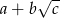 , gdzie
, gdzie 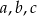 są liczbami naturalnymi.
są liczbami naturalnymi.
W równoległoboku 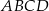 przekątna
przekątna 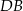 ma długość 7. Wiedząc, że obwód równoległoboku wynosi 26,
ma długość 7. Wiedząc, że obwód równoległoboku wynosi 26, 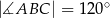 , oblicz długości boków równoległoboku.
, oblicz długości boków równoległoboku.
Dany jest równoległobok 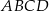 , w którym kąt rozwarty
, w którym kąt rozwarty 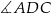 ma miarę
ma miarę 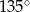 . Ponadto wiadomo, że
. Ponadto wiadomo, że 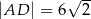 i
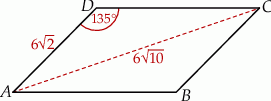
i 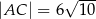 (zobacz rysunek). Oblicz obwód tego równoległoboku.
(zobacz rysunek). Oblicz obwód tego równoległoboku.
Punkty 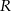 i
i 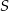 są środkami boków odpowiednio
są środkami boków odpowiednio 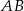 i
i 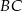 równoległoboku
równoległoboku 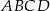 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 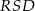 jest równe
jest równe pola tego równoległoboku.
pola tego równoległoboku.

