Kąt ostry między przekątnymi równoległoboku 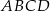 ma miarę
ma miarę 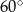 . Przekątna
. Przekątna 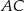 ma długość 6, a przekątna
ma długość 6, a przekątna 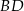 jest prostopadła do boku
jest prostopadła do boku 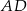 . Oblicz długości boków równoległoboku.
. Oblicz długości boków równoległoboku.
/Szkoła średnia/Geometria/Planimetria/Czworokąt/Równoległobok
Długości boków równoległoboku 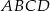 wynoszą 1 i
wynoszą 1 i 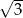 , a kąt przy wierzchołku
, a kąt przy wierzchołku 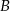 ma miarę
ma miarę 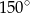 . Oblicz promień okręgu opisanego na trójkącie
. Oblicz promień okręgu opisanego na trójkącie 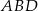 .
.
Niech  i
i 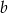 będą długościami kolejnych boków równoległoboku
będą długościami kolejnych boków równoległoboku 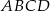 , zaś
, zaś 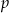 i
i  długościami jego przekątnych. Wykaż, że
długościami jego przekątnych. Wykaż, że 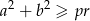 .
.
Czworokąt 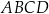 jest równoległobokiem. Wykaż, że jeżeli okręgi o średnicach
jest równoległobokiem. Wykaż, że jeżeli okręgi o średnicach 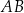 i
i 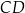 są styczne zewnętrznie, to równoległobok
są styczne zewnętrznie, to równoległobok 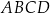 jest rombem.
jest rombem.
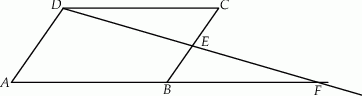
Prosta przechodząca przez wierzchołek 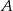 równoległoboku
równoległoboku 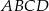 przecina jego przekątną
przecina jego przekątną 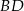 w punkcie
w punkcie 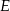 i bok
i bok 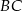 w punkcie
w punkcie 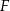 , a prostą
, a prostą 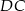 w punkcie
w punkcie 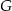 . Udowodnij, że
. Udowodnij, że
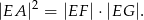
Długości boków równoległoboku są równe 6 i 10, a jego pole wynosi 36. Oblicz długości przekątnych tego równoległoboku.
Długości boków równoległoboku są równe 13 i 21, a jego pole wynosi 252. Oblicz długości przekątnych tego równoległoboku.
Dany jest równoległobok, którego obwód jest równy 50 cm. Stosunek długości jego wysokości wynosi 2:3, a stosunek miar jego kątów wewnętrznych jest równy 1:2. Oblicz długości boków i wysokości tego równoległoboku.
Wykaż, że proste przechodzące przez wierzchołek równoległoboku i środki boków, do których on nie należy, dzielą przekątną równoległoboku na trzy równe części.
Wykaż, że w dowolnym równoległoboku suma kwadratów długości przekątnych jest równa sumie kwadratów długości wszystkich boków.
Przekątna 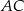 równoległoboku
równoległoboku 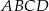 tworzy z jego bokami kąty o miarach
tworzy z jego bokami kąty o miarach 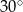 i
i 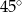 . Oblicz stosunek
. Oblicz stosunek 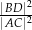 kwadratów długości przekątnych tego równoległoboku.
kwadratów długości przekątnych tego równoległoboku.
Dany jest równoległobok 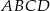 . Okrąg wpisany w trójkąt
. Okrąg wpisany w trójkąt 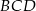 jest styczny do przekątnej
jest styczny do przekątnej 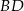 w punkcie
w punkcie 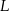 , a okrąg wpisany w trójkąt
, a okrąg wpisany w trójkąt 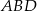 ma środek
ma środek 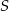 i jest styczny do boku
i jest styczny do boku 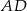 w punkcie
w punkcie 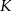 .
.
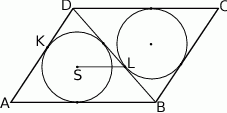
Wykaż, że jeżeli odcinek 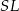 jest równoległy do prostej
jest równoległy do prostej 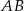 , to
, to 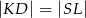 .
.
Przekątne równoległoboku 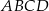 mają długości:
mają długości: 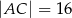 oraz
oraz 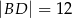 . Wierzchołki
. Wierzchołki 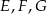 oraz
oraz 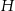 rombu
rombu 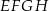 leżą na bokach równoległoboku
leżą na bokach równoległoboku 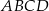 (zobacz rysunek). Boki tego rombu są równoległe do przekątnych równoległoboku.
(zobacz rysunek). Boki tego rombu są równoległe do przekątnych równoległoboku.
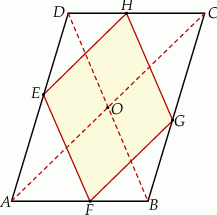
Oblicz długość boku rombu 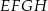 .
.
Wykazać, że odcinki łączące kolejne środki kwadratów zbudowanych na bokach równoległoboku tworzą także kwadrat.
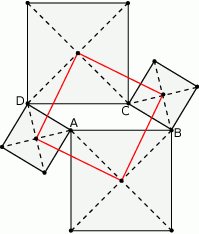
Krótsza przekątna równoległoboku tworzy bokami kąty  i
i 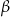 . Oblicz stosunek długości boków tego równoległoboku.
. Oblicz stosunek długości boków tego równoległoboku.
W równoległoboku, który nie jest prostokątem, krótsza przekątna dzieli go na dwa równoramienne trójkąty prostokątne. Krótszy bok równoległoboku ma długość 8. Oblicz pole tego równoległoboku.
W równoległoboku 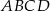 kąt ostry
kąt ostry 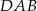 ma miarę
ma miarę 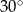 , zaś dłuższy bok ma długość 8. Promień okręgu opisanego na trójkącie
, zaś dłuższy bok ma długość 8. Promień okręgu opisanego na trójkącie 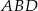 ma długość 4. Oblicz pole równoległoboku.
ma długość 4. Oblicz pole równoległoboku.
Dłuższa przekątna równoległoboku o kącie ostrym 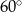 ma długość
ma długość 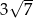 . Różnica długości jego boków wynosi 3. Oblicz pole tego równoległoboku i długość krótszej przekątnej.
. Różnica długości jego boków wynosi 3. Oblicz pole tego równoległoboku i długość krótszej przekątnej.
W równoległoboku 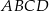 miara kąta ostrego jest równa
miara kąta ostrego jest równa 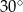 , a odległości punktu przecięcia się przekątnych od sąsiednich boków równoległoboku są równe 2 i
, a odległości punktu przecięcia się przekątnych od sąsiednich boków równoległoboku są równe 2 i 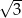 . Oblicz długość krótszej przekątnej tego równoległoboku.
. Oblicz długość krótszej przekątnej tego równoległoboku.
W równoległoboku 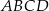 punkt
punkt 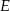 jest takim punktem boku
jest takim punktem boku 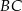 , że
, że 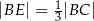 . Z wierzchołka
. Z wierzchołka 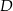 poprowadzono prostą przecinającą bok
poprowadzono prostą przecinającą bok 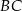 w punkcie
w punkcie 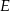 . Proste
. Proste 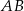 i
i 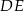 przecinają się w punkcie
przecinają się w punkcie 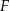 (zobacz rysunek). Wykaż, że pole trójkąta
(zobacz rysunek). Wykaż, że pole trójkąta 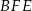 stanowi
stanowi 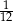 pola równoległoboku
pola równoległoboku 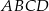 .
.
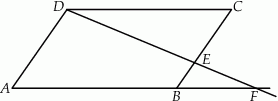
Punkt 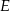 jest środkiem boku
jest środkiem boku 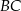 równoległoboku
równoległoboku 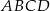 , a odcinek
, a odcinek  przecina przekątną
przecina przekątną 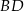 w punkcie
w punkcie 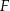 . Wykaż, że
. Wykaż, że 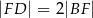 .
.
W równoległoboku 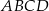 punkt
punkt 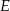 jest środkiem boku
jest środkiem boku 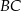 . Z wierzchołka
. Z wierzchołka 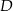 poprowadzono prostą przecinającą bok
poprowadzono prostą przecinającą bok 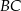 w punkcie
w punkcie 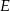 . Proste
. Proste 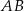 i
i 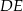 przecinają się w punkcie
przecinają się w punkcie 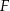 (zobacz rysunek). Wykaż, że punkt
(zobacz rysunek). Wykaż, że punkt 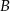 jest środkiem odcinka
jest środkiem odcinka 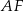 .
.