Dany jest trójmian kwadratowy 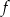 o współczynniku 2 przy najwyższej potędze
o współczynniku 2 przy najwyższej potędze  . Wierzchołek paraboli będącej wykresem tego trójmianu ma współrzędne
. Wierzchołek paraboli będącej wykresem tego trójmianu ma współrzędne 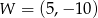 . Oblicz
. Oblicz 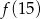 .
.
/Szkoła średnia/Funkcje/Kwadratowa
Funkcja kwadratowa 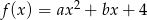 , osiąga wartości ujemne wtedy i tylko wtedy, gdy
, osiąga wartości ujemne wtedy i tylko wtedy, gdy 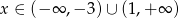 .
.
- Wyznacz wartości współczynników
 i
i 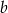 .
. - Napisz postać kanoniczną funkcji
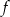 .
. - Podaj wzór funkcji kwadratowej
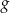 , której wykres otrzymamy przesuwając wykres funkcji
, której wykres otrzymamy przesuwając wykres funkcji 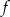 o wektor
o wektor ![→ u = [2,− 130]](https://img.zadania.info/zad/9353293/HzadT7x.gif) .
. - Wyznacz te argumenty
 , dla których
, dla których 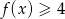 .
.
Funkcja kwadratowa 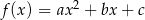 , spełnia warunek
, spełnia warunek 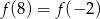 . Wykaż, że dla dowolnej liczby rzeczywistej
. Wykaż, że dla dowolnej liczby rzeczywistej  , spełniony jest warunek
, spełniony jest warunek 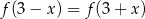 .
.
Funkcja 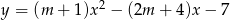 jest malejąca w zbiorze
jest malejąca w zbiorze 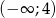 i rosnąca w zbiorze
i rosnąca w zbiorze 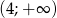 . Wyznacz parametr
. Wyznacz parametr 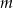 .
.
Dana jest funkcja 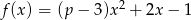 . Wyznacz te wartości parametru
. Wyznacz te wartości parametru 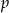 , dla których:
, dla których:
- największa wartość funkcji
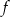 jest liczbą ujemną,
jest liczbą ujemną, - najmniejsza wartość funkcji
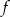 jest mniejsza od -2.
jest mniejsza od -2.
Wyznacz wzór funkcji 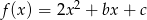 w postaci kanonicznej wiedząc, że jej miejsca zerowe są rozwiązaniami równania
w postaci kanonicznej wiedząc, że jej miejsca zerowe są rozwiązaniami równania 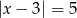 .
.
Ukryj
Podobne zadania
Wyznacz wzór funkcji 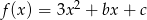 w postaci kanonicznej wiedząc, że jej miejsca zerowe są rozwiązaniami równania
w postaci kanonicznej wiedząc, że jej miejsca zerowe są rozwiązaniami równania 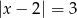 .
.
Wyznacz wartość funkcji 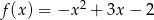 dla argumentu
dla argumentu 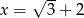 .
.
Ukryj
Podobne zadania
Wyznacz wartość funkcji 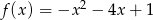 dla
dla 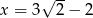 .
.
Wyznacz wszystkie całkowite wartości 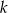 , dla których funkcja
, dla których funkcja 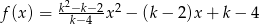 osiąga minimum i ma dwa różne miejsca zerowe.
osiąga minimum i ma dwa różne miejsca zerowe.

