Liczba 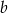 jest największą liczbą całkowitą, dla której najmniejsza wartość funkcji
jest największą liczbą całkowitą, dla której najmniejsza wartość funkcji 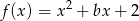 jest większa od
jest większa od 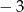 . Wyznacz liczbę
. Wyznacz liczbę 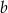 .
.
/Szkoła średnia/Funkcje/Kwadratowa
Funkcja kwadratowa określona wzorem 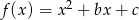 osiąga wartości ujemne wtedy i tylko wtedy, gdy
osiąga wartości ujemne wtedy i tylko wtedy, gdy 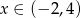 .
.
- Wyznacz wartości współczynników
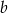 i
i  .
. - Oblicz, dla jakich argumentów
 , wartości funkcji
, wartości funkcji 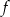 są mniejsze od wartości funkcji kwadratowej
są mniejsze od wartości funkcji kwadratowej 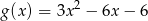 .
. - Rozwiąż równanie
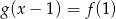 .
.
Wyznacz te wartości parametru 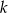 , dla których funkcja
, dla których funkcja 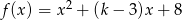 jest malejąca w przedziale
jest malejąca w przedziale 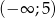 i rosnąca w przedziale
i rosnąca w przedziale 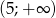 .
.
Sprowadź do postaci kanonicznej funkcję kwadratową daną w postaci ogólnej wzorem 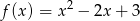 .
.
Sprowadź do postaci kanonicznej funkcję kwadratową daną w postaci iloczynowej wzorem 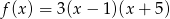 .
.
Sprowadź do postaci kanonicznej funkcję kwadratową daną w postaci ogólnej wzorem 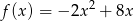 .
.
Sprowadź do postaci kanonicznej funkcję kwadratową daną w postaci ogólnej wzorem 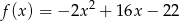 .
.
Sprowadź do postaci kanonicznej funkcję kwadratową daną w postaci ogólnej wzorem 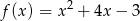 .
.
Sprowadź do postaci kanonicznej funkcję kwadratową daną w postaci ogólnej wzorem 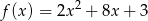 .
.
Sprowadź do postaci kanonicznej funkcję kwadratową daną w postaci ogólnej wzorem 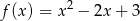 .
.
Wyznacz zbiór wartości funkcji 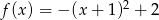 .
.
Wyznacz zbiór wartości funkcji 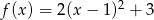 .
.
Wyznacz najmniejszą i największą wartość funkcji: 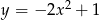 w przedziale
w przedziale 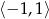 .
.
Wyznacz zbiór wartości funkcji 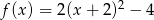 .
.
Właściciel pewnej apteki przeanalizował dane dotyczące liczby obsługiwanych klientów z 30 kolejnych dni. Przyjmijmy, że liczbę 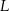 obsługiwanych klientów
obsługiwanych klientów  –tego dnia opisuje funkcja
–tego dnia opisuje funkcja
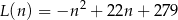
gdzie  jest liczbą naturalną spełniającą warunki
jest liczbą naturalną spełniającą warunki 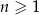 i
i 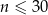 . Którego dnia analizowanego okresu w aptece obsłużono największą liczbę klientów? Oblicz liczbę klientów obsłużonych tego dnia.
. Którego dnia analizowanego okresu w aptece obsłużono największą liczbę klientów? Oblicz liczbę klientów obsłużonych tego dnia.
Wyznacz najmniejszą i największą wartość funkcji 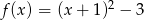 w przedziale
w przedziale 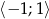 .
.
Funkcja kwadratowa 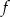 określona jest wzorem
określona jest wzorem 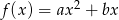 . Wiadomo, że
. Wiadomo, że 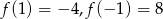 . Określ, dla jakich argumentów spełniona jest nierówność
. Określ, dla jakich argumentów spełniona jest nierówność 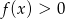 .
.
Dane są dwie funkcje kwadratowe 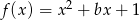 oraz
oraz 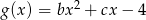 , gdzie
, gdzie 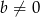 . Wyznacz wszystkie wartości parametrów
. Wyznacz wszystkie wartości parametrów 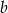 i
i  tak, aby funkcja
tak, aby funkcja 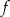 miała jedno miejsce zerowe i jednocześnie funkcja
miała jedno miejsce zerowe i jednocześnie funkcja 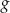 przyjmowała wartości ujemne dla każdego
przyjmowała wartości ujemne dla każdego 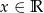 .
.
Wyznacz wzór ogólny funkcji kwadratowej, której największą wartością jest 2, a miejscami zerowymi są liczby 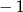 i 3.
i 3.
Wyznacz wzór ogólny funkcji kwadratowej, której najmniejszą wartością jest 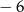 , a miejscami zerowymi są liczby
, a miejscami zerowymi są liczby 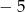 i 3.
i 3.
Funkcja 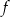 jest określona wzorem
jest określona wzorem 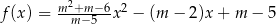 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz całkowite wartości parametru
. Wyznacz całkowite wartości parametru 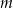 , dla których funkcja
, dla których funkcja 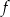 przyjmuje wartość największą i ma dwa różne miejsca zerowe o jednakowych znakach.
przyjmuje wartość największą i ma dwa różne miejsca zerowe o jednakowych znakach.
Funkcja kwadratowa 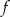 jest określona wzorem
jest określona wzorem 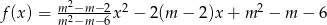 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 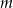 , dla których rozwiązaniem nierówności
, dla których rozwiązaniem nierówności 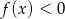 jest przedział postaci
jest przedział postaci 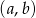 , gdzie
, gdzie 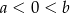 .
.
Funkcja 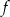 jest określona wzorem
jest określona wzorem 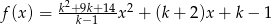 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz całkowite wartości parametru
. Wyznacz całkowite wartości parametru 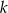 , dla których funkcja
, dla których funkcja 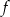 przyjmuje wartość największą i ma dwa różne miejsca zerowe o jednakowych znakach.
przyjmuje wartość największą i ma dwa różne miejsca zerowe o jednakowych znakach.
Funkcja kwadratowa 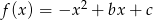 ma dwa miejsca zerowe:
ma dwa miejsca zerowe: 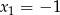 i
i 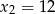 . Oblicz największą wartość tej funkcji.
. Oblicz największą wartość tej funkcji.
Funkcja kwadratowa 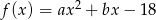 ma dwa miejsca zerowe:
ma dwa miejsca zerowe: 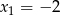 i
i 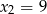 . Oblicz najmniejszą wartość tej funkcji.
. Oblicz najmniejszą wartość tej funkcji.
Wyznacz najmniejszą wartość funkcji kwadratowej 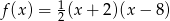 w przedziale
w przedziale 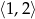 .
.
Funkcja kwadratowa jest określona wzorem 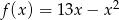 . Oblicz największą wartość funkcji
. Oblicz największą wartość funkcji 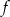 w przedziale
w przedziale 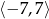 .
.
Funkcja kwadratowa jest określona wzorem 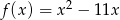 . Oblicz najmniejszą wartość funkcji
. Oblicz najmniejszą wartość funkcji 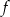 w przedziale
w przedziale 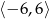 .
.
Wyznacz najmniejszą wartość funkcji 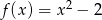 w przedziale
w przedziale 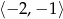 .
.
Funkcja 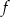 określona wzorem
określona wzorem 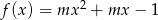 . Wyznacz te wartości parametru
. Wyznacz te wartości parametru 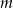 , dla których:
, dla których:
- funkcja
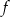 przyjmuje tylko wartości ujemne,
przyjmuje tylko wartości ujemne, - zbiorem wartości funkcji
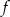 jest przedział
jest przedział 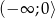 .
.
Funkcja kwadratowa 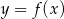 przyjmuje wartości ujemne tylko dla
przyjmuje wartości ujemne tylko dla 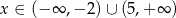 , a jej zbiorem wartości jest przedział
, a jej zbiorem wartości jest przedział 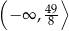 . Zapisz wzór funkcji kwadratowej
. Zapisz wzór funkcji kwadratowej 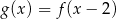 w postaci ogólnej.
w postaci ogólnej.
Funkcja kwadratowa 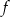 określona jest wzorem
określona jest wzorem 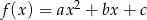 . Zbiorem rozwiązań nierówności
. Zbiorem rozwiązań nierówności 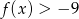 jest przedział
jest przedział 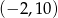 , a zbiorem rozwiązań nierówności
, a zbiorem rozwiązań nierówności 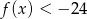 jest zbiór
jest zbiór 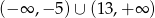 . Oblicz współczynniki
. Oblicz współczynniki 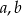 i
i  funkcji
funkcji 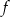 .
.
Wyznacz współczynniki funkcji kwadratowej 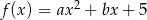 wiedząc, że
wiedząc, że 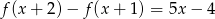 .
.
Wyznacz współczynniki funkcji kwadratowej 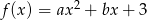 wiedząc, że
wiedząc, że 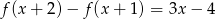 .
.
Dana jest funkcja 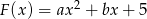 . Wyznacz
. Wyznacz  i
i 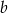 wiedząc, że
wiedząc, że 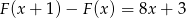 .
.
Funkcję kwadratową 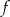 można opisać wzorem mającym postać
można opisać wzorem mającym postać 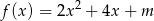 .
.
- Wyznacz warunek, dla którego funkcja
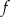 ma dwa różne pierwiastki
ma dwa różne pierwiastki 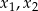 , a następnie oblicz
, a następnie oblicz 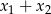 .
. - Wiedząc dodatkowo, że
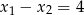 , oblicz
, oblicz 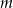 . Dla wyznaczonej liczby
. Dla wyznaczonej liczby 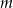 naszkicuj wykres funkcji
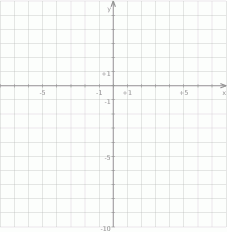
naszkicuj wykres funkcji 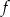 w układzie współrzędnych, a następnie rozwiąż równanie
w układzie współrzędnych, a następnie rozwiąż równanie 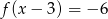 .
. 
Funkcja kwadratowa 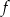 ma następujące własności:
ma następujące własności:
– zbiorem wartości funkcji 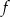 jest przedział
jest przedział 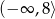 ;
;
– funkcja 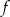 jest rosnąca w przedziale
jest rosnąca w przedziale 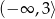 i malejąca w przedziale
i malejąca w przedziale 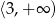 ;
;
– wykres funkcji 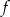 przecina oś
przecina oś 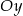 w punkcie, którego rzędna jest równa
w punkcie, którego rzędna jest równa 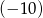 .
.
Wyznacz wzór funkcji 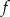 w postaci iloczynowej.
w postaci iloczynowej.
Wyznacz najmniejszą i największą wartość funkcji 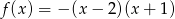 w przedziale
w przedziale 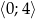 .
.
Oblicz najmniejszą i największą wartość funkcji kwadratowej 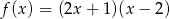 w przedziale
w przedziale 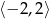 .
.
Wyznacz najmniejszą i największą wartość funkcji 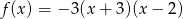 w przedziale
w przedziale 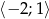 .
.
Wyznacz najmniejszą i największą wartość funkcji 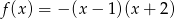 w przedziale
w przedziale 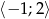 .
.

