Funkcja kwadratowa 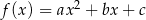 ma dwa miejsca zerowe
ma dwa miejsca zerowe 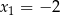 i
i 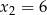 . Wykres funkcji
. Wykres funkcji 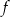 przechodzi przez punkt
przechodzi przez punkt 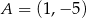 . Oblicz najmniejszą wartość funkcji
. Oblicz najmniejszą wartość funkcji 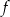 .
.
/Szkoła średnia/Funkcje/Kwadratowa
Parabola, która jest wykresem funkcji kwadratowej 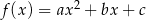 , przechodzi przez punkt
, przechodzi przez punkt 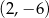 oraz
oraz 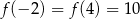 . Oblicz odległość wierzchołka tej paraboli od początku układu współrzędnych.
. Oblicz odległość wierzchołka tej paraboli od początku układu współrzędnych.
Funkcja kwadratowa 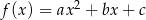 ma dwa miejsca zerowe
ma dwa miejsca zerowe 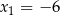 i
i 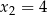 . Wykres funkcji
. Wykres funkcji 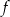 przechodzi przez punkt
przechodzi przez punkt 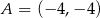 . Oblicz najmniejszą wartość funkcji
. Oblicz najmniejszą wartość funkcji 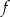 .
.
Wykresem funkcji kwadratowej 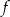 określonej wzorem
określonej wzorem 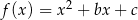 jest parabola, na której leży punkt
jest parabola, na której leży punkt 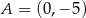 . Osią symetrii tej paraboli jest prosta o równaniu
. Osią symetrii tej paraboli jest prosta o równaniu 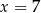 . Oblicz wartości współczynników
. Oblicz wartości współczynników 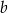 i
i  .
.
Wykresem funkcji kwadratowej 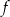 określonej wzorem
określonej wzorem 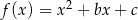 jest parabola, na której leży punkt
jest parabola, na której leży punkt 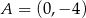 . Osią symetrii tej paraboli jest prosta o równaniu
. Osią symetrii tej paraboli jest prosta o równaniu 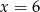 . Oblicz wartości współczynników
. Oblicz wartości współczynników 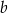 i
i  .
.
Osią symetrii wykresu funkcji kwadratowej 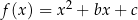 jest prosta o równaniu
jest prosta o równaniu 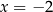 . Jednym z miejsc zerowych funkcji
. Jednym z miejsc zerowych funkcji 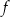 jest liczba 1. Oblicz współczynniki
jest liczba 1. Oblicz współczynniki 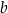 oraz
oraz  .
.
Dana jest rodzina funkcji kwadratowych zmiennej rzeczywistej  , opisana wzorem
, opisana wzorem 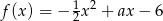 , gdzie
, gdzie  jest liczbą rzeczywistą.
jest liczbą rzeczywistą.
- Dla
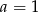 wyznacz zbiór tych argumentów, dla których funkcja
wyznacz zbiór tych argumentów, dla których funkcja 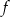 przyjmuje wartości większe niż funkcja liniowa
przyjmuje wartości większe niż funkcja liniowa 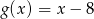 .
. - Wyznacz liczbę
 , dla której zbiorem wartości funkcji
, dla której zbiorem wartości funkcji 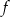 jest przedział
jest przedział 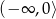 .
. - Dla
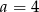 napisz wzór funkcji
napisz wzór funkcji 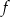 w postaci kanonicznej i narysuj jej wykres.
w postaci kanonicznej i narysuj jej wykres.
Funkcja 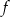 określona jest wzorem
określona jest wzorem 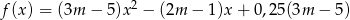 . Wyznacz te wartości parametru
. Wyznacz te wartości parametru 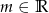 , dla których najmniejsza wartość funkcji
, dla których najmniejsza wartość funkcji 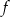 jest liczbą dodatnią.
jest liczbą dodatnią.
Do wykresu pewnej funkcji kwadratowej 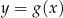 należy punkt o współrzędnych
należy punkt o współrzędnych 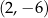 . Osią symetrii wykresu tej funkcji jest prosta o równaniu
. Osią symetrii wykresu tej funkcji jest prosta o równaniu 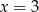 , a jednym z miejsc zerowych funkcji
, a jednym z miejsc zerowych funkcji 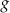 jest
jest 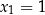 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 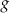 w postaci iloczynowej.
w postaci iloczynowej.
Funkcja kwadratowa 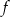 przyjmuje największą wartość równą
przyjmuje największą wartość równą 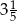 , a zbiorem rozwiązań nierówności
, a zbiorem rozwiązań nierówności 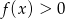 jest przedział
jest przedział 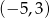 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 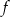 w postaci ogólnej.
w postaci ogólnej.
Funkcja kwadratowa 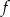 ma tylko jedno miejsce zerowe, przyjmuje największą wartość dla argumentu
ma tylko jedno miejsce zerowe, przyjmuje największą wartość dla argumentu 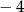 , a do jej wykresu należy punkt
, a do jej wykresu należy punkt 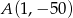 . Napisz wzór funkcji
. Napisz wzór funkcji 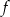 w postaci ogólnej.
w postaci ogólnej.
Funkcja kwadratowa 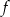 ma tylko jedno miejsce zerowe, przyjmuje największą wartość dla argumentu
ma tylko jedno miejsce zerowe, przyjmuje największą wartość dla argumentu 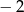 , a do jej wykresu należy punkt
, a do jej wykresu należy punkt 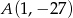 . Napisz wzór funkcji
. Napisz wzór funkcji 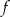 w postaci ogólnej.
w postaci ogólnej.
Funkcja kwadratowa 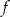 określona jest wzorem
określona jest wzorem 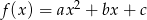 . Zbiorem rozwiązań nierówności
. Zbiorem rozwiązań nierówności 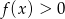 jest przedział
jest przedział 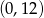 . Największa wartość funkcji
. Największa wartość funkcji 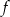 jest równa 9. Oblicz współczynniki
jest równa 9. Oblicz współczynniki  i
i  funkcji
funkcji 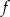 .
.
Funkcja kwadratowa 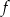 określona jest wzorem
określona jest wzorem 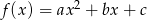 . Zbiorem rozwiązań nierówności
. Zbiorem rozwiązań nierówności 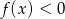 jest przedział
jest przedział 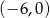 . Najmniejsza wartość funkcji
. Najmniejsza wartość funkcji 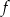 jest równa
jest równa 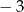 . Oblicz współczynniki
. Oblicz współczynniki 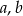 i
i  funkcji
funkcji 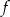 .
.
Zapisz wzór funkcji 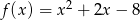 w postaci iloczynowej.
w postaci iloczynowej.
Zapisz wzór funkcji 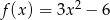 w postaci iloczynowej.
w postaci iloczynowej.
Zapisz wzór funkcji 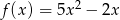 w postaci iloczynowej.
w postaci iloczynowej.
Funkcja kwadratowa 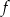 jest określona dla wszystkich liczb rzeczywistych
jest określona dla wszystkich liczb rzeczywistych  wzorem
wzorem 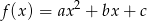 . Największa wartość funkcji
. Największa wartość funkcji 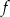 jest równa 6 oraz
jest równa 6 oraz 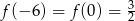 . Oblicz wartość współczynnika
. Oblicz wartość współczynnika  .
.
Funkcja kwadratowa 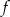 jest określona dla wszystkich liczb rzeczywistych
jest określona dla wszystkich liczb rzeczywistych  wzorem
wzorem 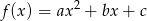 . Najmniejsza wartość funkcji
. Najmniejsza wartość funkcji 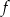 jest równa
jest równa 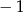 oraz
oraz 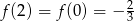 . Oblicz wartość współczynnika
. Oblicz wartość współczynnika  .
.
Wykaż, że jeżeli 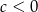 , to trójmian kwadratowy
, to trójmian kwadratowy 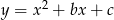 ma dwa różne miejsca zerowe.
ma dwa różne miejsca zerowe.
Dane są dwie funkcje kwadratowe 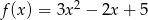 i
i 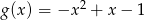 . Wyznacz największą wartość funkcji
. Wyznacz największą wartość funkcji 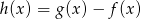 .
.
Zbadaj, na podstawie definicji, monotoniczność funkcji 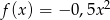 w zbiorze
w zbiorze 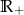 .
.
Zbadaj, na podstawie definicji, monotoniczność funkcji 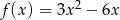 w zbiorze
w zbiorze 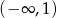 .
.
Zbadaj, na podstawie definicji, monotoniczność funkcji 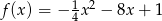 w zbiorze
w zbiorze 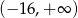 .
.
Liczby 1 i 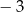 są miejscami zerowymi funkcji kwadratowej
są miejscami zerowymi funkcji kwadratowej 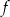 oraz do jej wykresu należy punkt
oraz do jej wykresu należy punkt 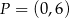 . Wyznacz wzór ogólny tej funkcji.
. Wyznacz wzór ogólny tej funkcji.
Liczby 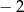 i
i 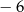 są miejscami zerowymi funkcji kwadratowej
są miejscami zerowymi funkcji kwadratowej 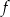 oraz do jej wykresu należy punkt
oraz do jej wykresu należy punkt 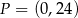 . Wyznacz wzór ogólny tej funkcji.
. Wyznacz wzór ogólny tej funkcji.
Jedynym miejscem zerowym funkcji kwadratowej 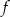 jest liczba 2. Wykres funkcji
jest liczba 2. Wykres funkcji 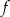 przecina oś
przecina oś 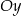 w punkcie o współrzędnych
w punkcie o współrzędnych 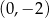 . Wyznacz wzór tej funkcji w postaci ogólnej.
. Wyznacz wzór tej funkcji w postaci ogólnej.
Funkcja kwadratowa 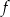 ma dokładnie jedno miejsce zerowe równe 2. Ponadto
ma dokładnie jedno miejsce zerowe równe 2. Ponadto 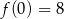 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 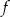 .
.
Funkcja kwadratowa 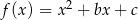 nie ma miejsc zerowych. Wykaż, że
nie ma miejsc zerowych. Wykaż, że 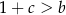 .
.
Wyznacz wszystkie wartości parametru 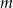 , dla których funkcja
, dla których funkcja 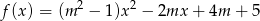 jest rosnąca w przedziale
jest rosnąca w przedziale 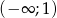 i malejąca w przedziale
i malejąca w przedziale 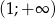 .
.
W poniższej tabeli podane są wartości funkcji kwadratowej 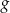 dla kilku wybranych argumentów zapisanych w kolejności rosnącej:
dla kilku wybranych argumentów zapisanych w kolejności rosnącej:
| x | -2 | -1 | 0 | 1 | |
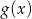 | -4 | 1 | 2 | -1 |
- Wyznacz wzór funkcji
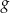 .
. - Uzupełnij brakujące zapisy w tabeli.
- Rozwiąż nierówność
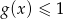 .
.
Wyznacz najmniejszą wartość funkcji 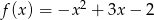 w przedziale
w przedziale 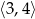 .
.
Oblicz największą wartość funkcji kwadratowej 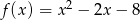 w przedziale
w przedziale 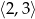 .
.
Wyznacz najmniejszą wartość funkcji 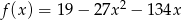 na przedziale
na przedziale 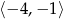 .
.
Oblicz najmniejszą wartość funkcji kwadratowej 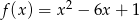 w przedziale
w przedziale 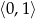 .
.
Wyznacz największą wartość funkcji 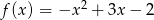 w przedziale
w przedziale 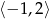 .
.
Oblicz najmniejszą wartość funkcji kwadratowej 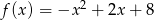 w przedziale
w przedziale 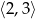 .
.
Oblicz największą wartość funkcji 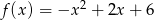 w przedziale
w przedziale 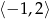 .
.
Liczby rzeczywiste  i
i  spełniają warunek
spełniają warunek 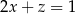 . Wyznacz takie wartości
. Wyznacz takie wartości  i
i  , dla których wyrażenie
, dla których wyrażenie 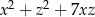 przyjmuje największą wartość. Podaj tę największą wartość.
przyjmuje największą wartość. Podaj tę największą wartość.
Liczby rzeczywiste 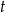 i
i 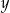 spełniają warunek
spełniają warunek 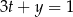 . Wyznacz takie wartości
. Wyznacz takie wartości 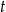 i
i 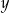 , dla których wyrażenie
, dla których wyrażenie 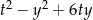 przyjmuje największą wartość. Podaj tę największą wartość.
przyjmuje największą wartość. Podaj tę największą wartość.

