Wyznacz najmniejszą i największą wartość funkcji 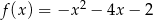 w przedziale
w przedziale 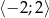 .
.
/Szkoła średnia/Funkcje/Kwadratowa
Wyznacz największą i najmniejszą wartość funkcji 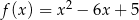 osiąganą w przedziale
osiąganą w przedziale 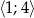 .
.
Wyznacz najmniejszą i największą wartość funkcji kwadratowej 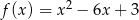 w przedziale
w przedziale 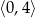 .
.
Oblicz najmniejszą i największą wartość funkcji 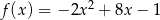 w przedziale
w przedziale 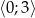 .
.
Wyznacz wartość największą i najmniejszą funkcji kwadratowej 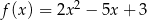 w przedziale
w przedziale 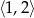 .
.
Wyznacz najmniejszą i największą wartość funkcji kwadratowej 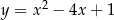 w przedziale
w przedziale 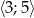 .
.
Oblicz najmniejszą i największą wartość funkcji kwadratowej 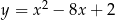 w przedziale
w przedziale 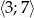 .
.
Oblicz najmniejszą i największą wartość funkcji kwadratowej 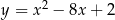 w przedziale
w przedziale 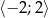 .
.
Wyznacz najmniejszą i największą wartość funkcji 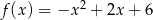 w przedziale
w przedziale 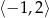 .
.
Oblicz najmniejszą i największą wartość funkcji 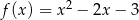 w przedziale
w przedziale 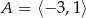 .
.
Oblicz najmniejszą i największą wartość funkcji 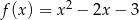 w przedziale
w przedziale 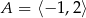 .
.
Wyznacz najmniejszą i największą wartość funkcji kwadratowej 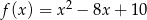 w przedziale
w przedziale 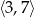 .
.
Wyznacz największą i najmniejszą wartość funkcji 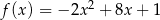 osiąganą w przedziale
osiąganą w przedziale 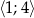 .
.
Wyznacz największą i najmniejszą wartość funkcji 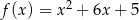 osiąganą w przedziale
osiąganą w przedziale 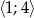 .
.
Oblicz największą i najmniejszą wartość funkcji 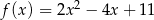 w przedziale
w przedziale 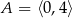 .
.
Oblicz najmniejszą i największą wartość funkcji 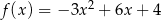 w przedziale
w przedziale 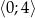 .
.
Określ zbiór wartości funkcji: 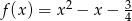 . Dla jakich argumentów funkcja przyjmuje wartości ujemne?
. Dla jakich argumentów funkcja przyjmuje wartości ujemne?
Dana jest funkcja kwadratowa 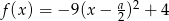
- Dla
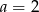 wyznacz postać iloczynową tej funkcji.
wyznacz postać iloczynową tej funkcji. - Dla
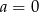 wyznacz te argumenty, dla których funkcja osiąga wartości ujemne.
wyznacz te argumenty, dla których funkcja osiąga wartości ujemne. - Wyznacz
 tak, aby osią symetrii wykresu funkcji była prosta o równaniu
tak, aby osią symetrii wykresu funkcji była prosta o równaniu 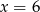 .
.
Podaj wartość wyrażenia 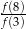 jeżeli
jeżeli 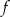 jest funkcją kwadratową o miejscach zerowych 2 i 4.
jest funkcją kwadratową o miejscach zerowych 2 i 4.
Liczby 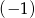 i 3 są miejscami zerowymi funkcji kwadratowej
i 3 są miejscami zerowymi funkcji kwadratowej 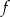 . Oblicz
. Oblicz 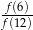 .
.
Miejscami zerowymi funkcji kwadratowej 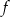 są liczby (-6) oraz 1. Oblicz wartość wyrażenia
są liczby (-6) oraz 1. Oblicz wartość wyrażenia 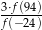 .
.
Określ zbiór wartości i przedziały monotoniczności funkcji 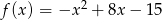 .
.
Określ zbiór wartości i przedziały monotoniczności funkcji 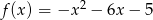 .
.
Wykresem funkcji kwadratowej 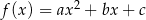 jest parabola styczna do prostej
jest parabola styczna do prostej 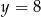 w punkcie
w punkcie 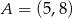 oraz przechodząca przez punkt
oraz przechodząca przez punkt 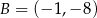 . Wyznacz wartości współczynników
. Wyznacz wartości współczynników 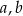 i
i  .
.
Jednym z miejsc zerowych funkcji kwadratowej 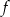 jest liczba 5, maksymalny przedział, w którym ta funkcja jest malejąca to
jest liczba 5, maksymalny przedział, w którym ta funkcja jest malejąca to 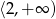 . Największa wartość funkcji
. Największa wartość funkcji 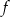 w przedziale
w przedziale 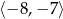 jest równa
jest równa 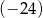 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 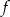 i narysuj jej wykres.
i narysuj jej wykres.
Funkcja kwadratowa 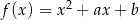 ma dwa miejsca zerowe, które różnią się o 7. Wykres funkcji
ma dwa miejsca zerowe, które różnią się o 7. Wykres funkcji 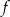 przechodzi przez punkt
przechodzi przez punkt 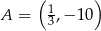 . Oblicz najmniejszą wartość funkcji
. Oblicz najmniejszą wartość funkcji 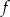 .
.
Wielomiany 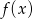 i
i 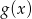 spełniają warunki
spełniają warunki 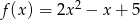 i
i 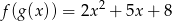 . Wyznacz wzór wielomianu
. Wyznacz wzór wielomianu 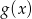 .
.
Sprowadź do postaci ogólnej funkcję kwadratową 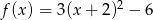 .
.
Sprowadź do postaci ogólnej funkcję kwadratową 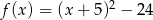 .
.
Sprowadź do postaci ogólnej funkcję kwadratową 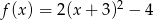 .
.
Sprowadź do postaci ogólnej funkcję kwadratową 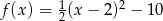 .
.
Sprowadź do postaci ogólnej funkcję kwadratową 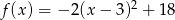 .
.
Zapisz wzór funkcji kwadratowej 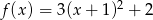 w postaci ogólnej.
w postaci ogólnej.
Sprowadź do postaci ogólnej funkcję kwadratową 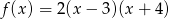 .
.
Właściciel pewnej pączkarni przeanalizował dane dotyczące liczby obsługiwanych klientów z 40 kolejnych dni. Przyjmijmy, że liczbę 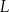 obsługiwanych klientów
obsługiwanych klientów  –tego dnia opisuje funkcja
–tego dnia opisuje funkcja
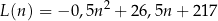
gdzie  jest liczbą naturalną spełniającą warunki
jest liczbą naturalną spełniającą warunki 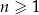 i
i 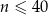 . Oblicz jaka była największa liczba klientów pączkarni obsłużonych jednego dnia w okresie poddanym analizie.
. Oblicz jaka była największa liczba klientów pączkarni obsłużonych jednego dnia w okresie poddanym analizie.
Wiesz, że funkcja kwadratowa 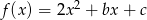 przyjmuje wartość najmniejszą
przyjmuje wartość najmniejszą 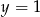 dla
dla 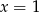 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 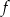 , a następnie rozwiąż równanie
, a następnie rozwiąż równanie 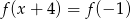 .
.
Wyznacz 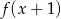 jeżeli
jeżeli 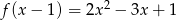 .
.
Zbiorem wartości funkcji kwadratowej 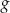 jest przedział
jest przedział 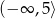 , a zbiorem rozwiązań nierówności
, a zbiorem rozwiązań nierówności 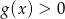 jest przedział
jest przedział 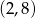 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 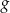 .
.
Określ zbiór wartości i przedziały monotoniczności funkcji 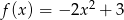 .
.
Określ zbiór wartości i przedziały monotoniczności funkcji 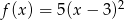 .
.
Określ zbiór wartości i przedziały monotoniczności funkcji 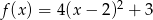 .
.
Napisz wzór i narysuj wykres funkcji 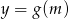 , która każdej liczbie rzeczywistej
, która każdej liczbie rzeczywistej 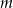 przyporządkowuje najmniejszą wartość funkcji kwadratowej
przyporządkowuje najmniejszą wartość funkcji kwadratowej 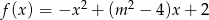 w przedziale
w przedziale 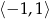 .
.
Znajdź taką wartość parametru 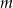 , aby największa wartość funkcji
, aby największa wartość funkcji 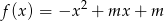 była najmniejsza z możliwych.
była najmniejsza z możliwych.
Dany jest trójmian kwadratowy 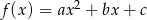 .
.
- Dla
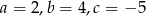 wyznacz największą i najmniejszą wartość tego trójmianu w przedziale
wyznacz największą i najmniejszą wartość tego trójmianu w przedziale 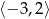 .
. - Wyznacz wzór trójmianu w postaci iloczynowej, jeśli wiadomo, że ma on miejsca zerowe
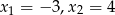 , a do jego wykresu należy punkt
, a do jego wykresu należy punkt 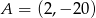 .
.
Właściciel pewnej piekarni przeanalizował dane dotyczące liczby obsługiwanych klientów z 28 kolejnych dni. Przyjmijmy, że liczbę 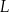 obsługiwanych klientów
obsługiwanych klientów  –tego dnia opisuje funkcja
–tego dnia opisuje funkcja
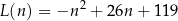
gdzie  jest liczbą naturalną spełniającą warunki
jest liczbą naturalną spełniającą warunki 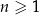 i
i 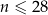 . W którym dniu analizowanego okresu w piekarni obsłużono największą, a w którym dniu najmniejszą liczbę klientów? Oblicz liczby klientów obsłużonych w tych dniach.
. W którym dniu analizowanego okresu w piekarni obsłużono największą, a w którym dniu najmniejszą liczbę klientów? Oblicz liczby klientów obsłużonych w tych dniach.
Zapisz wzór funkcji 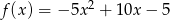 w postaci kanonicznej i iloczynowej.
w postaci kanonicznej i iloczynowej.

