Makau jest jednym z najbardziej zaludnionych krajów świata, powierzchnię 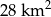 zamieszkuje 545674 ludzi. Na
zamieszkuje 545674 ludzi. Na 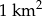 powierzchni tego kraju żyje więc średnio około
powierzchni tego kraju żyje więc średnio około
A) 20000 osób B) 15000 osób C) 10000 osób D) 2000 osób
/Szkoła podstawowa
Mongolia jest jednym z najsłabiej zaludnionych krajów świata powierzchnię 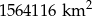 zamieszkuje 2,99 mln ludzi. Na
zamieszkuje 2,99 mln ludzi. Na 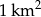 powierzchni tego kraju żyje więc średnio około
powierzchni tego kraju żyje więc średnio około
A) 0,5 osoby B) 2 osoby C) 8 osób D) 16 osób
Australia jest jednym z najsłabiej zaludnionych krajów świata powierzchnię 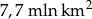 zamieszkuje 22 mln ludzi. Na
zamieszkuje 22 mln ludzi. Na 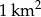 powierzchni tego kraju żyje więc średnio około
powierzchni tego kraju żyje więc średnio około
A) 1 osoba B) 2 osoby C) 3 osoby D) 30 osób
Z miejscowości Ząbki do miejscowości Bródka wyruszyły dwa samochody – pierwszym jechał pan Bogdan, drugim pan Wojciech. Każdy z tych dwóch samochodów pokonał całą trasę w tym samym czasie, przy czym pan Wojciech jechał cały czas ze stałą prędkością, a pan Bogdan pierwsze 25 km trasy pokonał w czasie 18 minut, kolejne 20 km pokonał w czasie 16 minut, a pozostałe 35 km trasy pokonał w pół godziny. Oblicz z jaką średnią prędkością samochód pana Wojciecha pokonał trasę między Ząbkami a Bródką. Wynik podaj w kilometrach na godzinę.
W trójkącie o kątach wewnętrznych 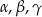 miara kąta
miara kąta  jest równa różnicy miar dwóch pozostałych kątów. Uzasadnij, że ten trójkąt jest prostokątny.
jest równa różnicy miar dwóch pozostałych kątów. Uzasadnij, że ten trójkąt jest prostokątny.
Ile jest trójkątów o obwodzie równym 19, w których długości boków wyrażone są liczbami całkowitymi. Wymień je.
Na loterię przygotowano 500 losów, wśród których jest 40 losów wygrywających. Każdy los wygrywający upoważnia do odbioru nagrody w wysokości 15 zł. Jak powinna być cena jednego losu, żeby przychód uzyskany ze sprzedaży wszystkich losów był wyższy od sumy wypłaconych nagród o 200 zł?
A) 1,2 zł B) 1,6 zł C) 2,6 zł D) 2,5 zł
Na loterię przygotowano 500 losów, wśród których jest 40 losów wygrywających. Każdy los wygrywający upoważnia do odbioru nagrody w wysokości 15 zł. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Pierwszych 17 losów zakupionych w loterii było przegrywających. Zuzia jako 18 osoba kupuje los w tej loterii. Prawdopodobieństwo, że los Zuzi jest wygrywający jest większe niż 0,08. | P | F |
| W drugiej edycji tej loterii zwiększono liczbę losów wygrywających dwukrotnie, a liczbę losów przegrywających pozostawiono bez zmian. Zatem prawdopodobieństwo wygranej wzrosło w drugiej edycji dwukrotnie. | P | F |
Piotrek na dużej kartce w kratkę narysował figurę złożoną z 60 połączonych odcinków, które kolejno ponumerował liczbami naturalnymi od 1 do 60. Wszystkie komórki kratki są takimi samymi kwadratami. Na rysunku przedstawiono fragment tej figury, złożony z 17 początkowych odcinków. Kolejne odcinki tej figury Piotrek narysował według tej samej reguły, którą zastosował do narysowania odcinków 1–17.
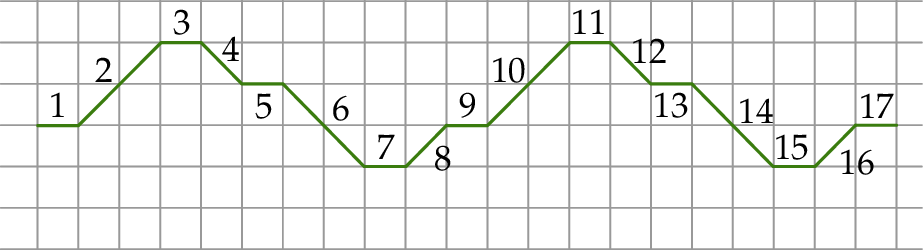
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Proste zawierające odcinki o numerach 39 oraz 53 są wzajemnie równoległe. | P | F |
| Proste zawierające odcinki o numerach 27 oraz 49 są wzajemnie prostopadłe. | P | F |
Pole wielokąta przedstawionego na rysunku opisuje wyrażenie algebraiczne
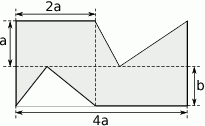
A) 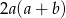 B)
B) 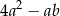 C)
C) 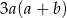 D)
D) 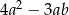
Do trzech jednakowych naczyń wlano tyle wody, że w pierwszym naczyniu woda zajmowała  pojemności, w drugim:
pojemności, w drugim:  pojemności, a w trzecim:
pojemności, a w trzecim:  pojemności danego naczynia.
pojemności danego naczynia.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| W drugim naczyniu było mniej wody niż w trzecim naczyniu. | P | F |
| W pierwszym i drugim naczyniu łącznie było tyle samo wody, co w trzecim naczyniu. | P | F |
Na bokach trójkąta prostokątnego 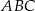 zaznaczono punkty
zaznaczono punkty 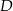 i
i 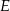 . Odcinek
. Odcinek 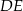 podzielił trójkąt
podzielił trójkąt 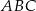 na dwa wielokąty: trójkąt prostokątny
na dwa wielokąty: trójkąt prostokątny 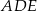 i czworokąt
i czworokąt 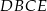 , jak na rysunku. Odcinek
, jak na rysunku. Odcinek 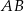 ma długość
ma długość 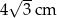 , a odcinek
, a odcinek 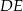 ma długość 3 cm.
ma długość 3 cm.
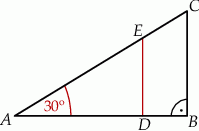
Długość odcinka 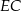 jest równa
jest równa
A) 1 cm B) 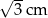 C) 2 cm D) 4 cm E)
C) 2 cm D) 4 cm E) 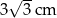
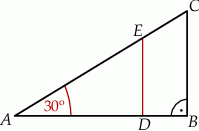
Na bokach trójkąta prostokątnego 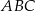 zaznaczono punkty
zaznaczono punkty 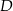 i
i 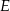 . Odcinek
. Odcinek 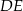 podzielił trójkąt
podzielił trójkąt 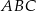 na dwa wielokąty: trójkąt prostokątny
na dwa wielokąty: trójkąt prostokątny 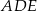 i czworokąt
i czworokąt 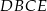 , jak na rysunku. Odcinek
, jak na rysunku. Odcinek 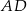 ma długość
ma długość 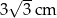 , a odcinek
, a odcinek 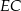 ma długość 2 cm.
ma długość 2 cm.
Długość odcinka 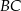 jest równa
jest równa
A) 6 cm B) 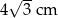 C) 2 cm D) 4 cm E)
C) 2 cm D) 4 cm E) 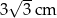
Odległość między punktami, które na osi liczbowej odpowiadają liczbom 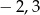 i
i 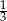 jest równa
jest równa
A) 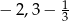 B)
B) 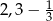 C)
C) 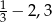 D)
D) 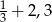
Odległość między punktami, które na osi liczbowej odpowiadają liczbom 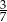 i
i 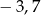 jest równa
jest równa
A) 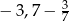 B)
B) 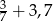 C)
C) 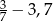 D)
D) 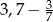
Liczba 1300 jest zaokrągleniem do rzędu setek różnych liczb naturalnych. Ile jest wszystkich liczb naturalnych różnych od 1300, które mają takie zaokrąglenie?
A) 100 B) 99 C) 49 D) 50
Z pudełka z metalowymi kulkami wyjęto najpierw 105 kulek, a potem 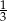 kulek, które pozostały w pudełku. W wyniku tych dwóch operacji liczba kulek w pudełku zmniejszyła się czterokrotnie. Ile kulek było początkowo w pudełku?
kulek, które pozostały w pudełku. W wyniku tych dwóch operacji liczba kulek w pudełku zmniejszyła się czterokrotnie. Ile kulek było początkowo w pudełku?
A) 171 B) 216 C) 168 D) 144
Podaną liczbę zapisz bez używana potęg: 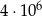 .
.
Podaną liczbę zapisz bez używania potęg: 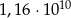 .
.
Podaną liczbę zapisz bez używania potęg: 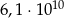 .
.
Podaną liczbę zapisz bez używania potęg: 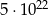 .
.
Podaną liczbę zapisz bez używana potęg: 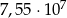 .
.
Ania jest 4 razy starsza od Pawła. Za 8 lat Ania i Paweł będą mieli w sumie 38 lat. Jeżeli przez  oznaczymy wiek Pawła, a przez
oznaczymy wiek Pawła, a przez 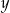 wiek Ani, to powyższą sytuację opisuje układ równań
wiek Ani, to powyższą sytuację opisuje układ równań
A) 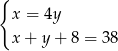 B)
B) 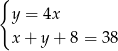 C)
C) 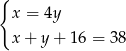 D)
D) 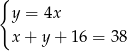
Staś ma dwa jednakowe klocki w kształcie ostrosłupa prawidłowego czworokątnego, każdy o polu powierzchni całkowitej 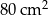 . Podstawa i ściana boczna klocka mają równe pola. Staś skleił oba klocki podstawami tak, jak na rysunku.
. Podstawa i ściana boczna klocka mają równe pola. Staś skleił oba klocki podstawami tak, jak na rysunku.
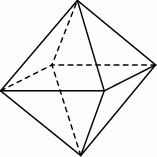
Jakie pole powierzchni ma bryła otrzymana przez Stasia?
A) 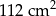 B)
B) 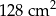 C)
C) 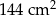 D)
D) 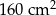
Kacper ma dwa jednakowe klocki w kształcie ostrosłupa prawidłowego sześciokątnego, każdy o polu powierzchni całkowitej 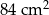 . Podstawa i ściana boczna klocka mają równe pola. Staś skleił oba klocki podstawami tak, jak na rysunku.
. Podstawa i ściana boczna klocka mają równe pola. Staś skleił oba klocki podstawami tak, jak na rysunku.
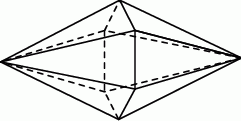
Jakie pole powierzchni ma bryła otrzymana przez Stasia?
A) 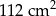 B)
B)  C)
C) 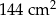 D)
D) 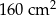
Średnia arytmetyczna zestawu danych: 2, 4, 7, 8,  jest równa
jest równa  , natomiast średnia arytmetyczna zestawu danych: 2, 4, 7, 8,
, natomiast średnia arytmetyczna zestawu danych: 2, 4, 7, 8,  ,
, 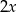 jest równa
jest równa 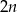 . Wynika stąd, że
. Wynika stąd, że
A) 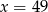 B)
B) 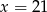 C)
C) 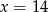 D)
D) 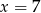
Średnia arytmetyczna zestawu danych: 1, 3, 6, 7,  jest równa
jest równa  , natomiast średnia arytmetyczna zestawu danych: 1, 3, 7, 7,
, natomiast średnia arytmetyczna zestawu danych: 1, 3, 7, 7,  ,
, 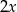 jest równa
jest równa 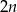 . Wynika stąd, że
. Wynika stąd, że
A) 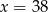 B)
B) 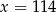 C)
C) 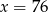 D)
D) 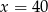
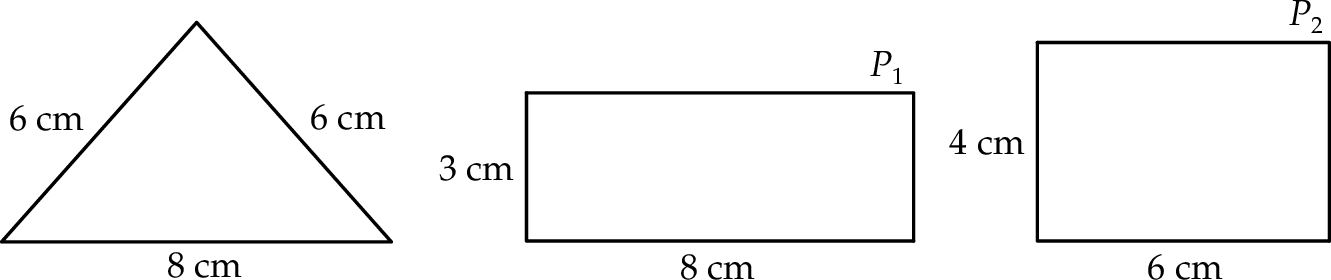
Na rysunku przedstawiono trójkąt i dwa prostokąty 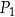 i
i 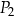 oraz podano długości ich boków.
oraz podano długości ich boków.
Czy te trzy wielokąty mogą być ścianami jednego graniastosłupa? Wybierz odpowiedź T lub N i jej uzasadnienie spośród zdań A–C.
| Tak | Nie |
| ponieważ | |
| A) | każdy z prostokątów 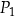 i i 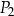 ma bok takiej samej długości jak jeden z boków trójkąta. ma bok takiej samej długości jak jeden z boków trójkąta. |
| B) | prostokąty 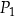 i i 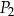 nie mają takich samych wymiarów. nie mają takich samych wymiarów. |
| C) | prostokąty 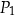 i i 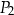 nie mają boku tej samej długości. nie mają boku tej samej długości. |
Samochód połowę drogi przebył ze średnią prędkością 30 km/h, a drugą połowę drogi ze średnią prędkością 60 km/h. Zatem średnia prędkość samochodu na całej trasie jest równa
A) 40 km/h B) 45 km/h C) 50 km/h D) 55 km/h
Rowerzysta połowę górskiej trasy pokonał ze średnią prędkością 8 km/h, a drugą połowę tej trasy pokonał ze średnią prędkością 24 km/h. Zatem średnia prędkość rowerzysty na całej trasie jest równa
A) 10 km/h B) 12 km/h C) 16 km/h D) 18 km/h
Zmieszano dwa gatunki kaw w stosunku 1:3 i otrzymano mieszankę w cenie 66 zł za kilogram. Po zmieszaniu tych kaw w odwrotnym stosunku otrzymano mieszankę w cenie 54 zł za kilogram. Jaka byłaby cena 1 kilograma mieszanki, gdyby zmieszano te kawy w stosunku 1:1?
Doświadczenie losowe polega na trzykrotnym rzucie monetą. Jeśli wypadnie orzeł, zapisujemy 5, a jeśli reszka – zapisujemy 4. Wynikiem doświadczenia jest zapisana liczba trzycyfrowa. Jakie jest prawdopodobieństwo, że zapisana liczba jest podzielna przez 6?
A) 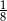 B)
B) 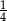 C)
C)  D)
D) 

