Pewien ostrosłup ma 16 wierzchołków. Ile wierzchołków ma graniastosłup o takiej samej podstawie, jaką ma ten ostrosłup?
A) 17 B) 30 C) 32 D) 45
/Szkoła podstawowa
Pewien ostrosłup ma 17 wierzchołków. Ile wierzchołków ma graniastosłup o takiej samej podstawie, jaką ma ten ostrosłup?
A) 17 B) 30 C) 32 D) 45
Oblicz promień okręgu o długości 4 cm.
Oblicz promień okręgu o długości 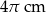 .
.
Oblicz promień okręgu o długości 2,4 dm.
Oblicz promień okręgu o długości 5 dm.
Oblicz promień okręgu o długości 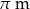 .
.
Oblicz promień okręgu o długości 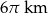 .
.
Średnia arytmetyczna zestawu danych: 7, 12, 8, 6,  ,
, 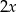 jest taka sama jak średnia arytmetyczna zestawu danych: 11, 8, 9, 3,
jest taka sama jak średnia arytmetyczna zestawu danych: 11, 8, 9, 3,  ,
,  ,
, 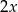 . Wynika stąd, że
. Wynika stąd, że
A) 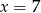 B)
B) 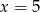 C)
C) 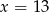 D)
D) 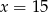
Od kartonika w kształcie trójkąta równobocznego odcięto naroża, tak jak pokazano na rysunku i otrzymano sześciokąt foremny o bokach długości 3.
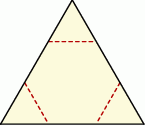
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Kartonik był trójkątem o obwodzie 27. | P | F |
| Suma pól odciętych naroży jest dwa razy mniejsza od pola sześciokąta. | P | F |
Oblicz wysokość trójkąta prostokątnego o przyprostokątnych 12 cm i 9 cm, która jest poprowadzona do przeciwprostokątnej.
Trójkąt prostokątny ma przyprostokątne długości 6 i 8. Wyznacz długość najkrótszej wysokości tego trójkąta.
Trójkąt prostokątny ma przyprostokątne długości 12 i 5. Wyznacz długość najkrótszej wysokości tego trójkąta.
Aby dobrać rozmiar ramy roweru do wzrostu użytkownika, można posłużyć się następującą regułą: rozmiar odpowiedniej ramy otrzymamy, gdy od 40% wzrostu użytkownika (w cm) odejmiemy 15 cm.
Jaki rozmiar powinna mieć, według tej reguły, rama dla rowerzysty o wzroście 175 cm?
A) 55 cm B) 64 cm C) 90 cm D) 96 cm
Aby dobrać rozmiar ramy roweru do wzrostu użytkownika, można posłużyć się następującą regułą: rozmiar odpowiedniej ramy otrzymamy, gdy od 40% wzrostu użytkownika (w cm) odejmiemy 15 cm.
Niech  oznacza rozmiar ramy (w cm),
oznacza rozmiar ramy (w cm), 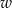 – wzrost użytkownika (też w cm).
– wzrost użytkownika (też w cm).
Którym wzorem nie można wyrazić opisanej wyżej reguły dobierania rozmiaru ramy?
A) 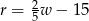 B)
B) 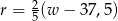 C)
C) 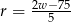 D)
D) 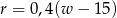
Dane są trzy liczby 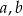 i
i  .
.
Gdy 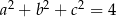 oraz
oraz  jest liczbą mniejszą od
jest liczbą mniejszą od 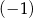 , to suma
, to suma 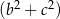 jest A/B.
jest A/B.
A) mniejsza od 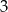 B) większa od
B) większa od 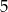
Gdy 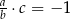 oraz
oraz 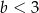 , to
, to 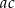 jest liczbą C/D.
jest liczbą C/D.
C) mniejszą od 3 D) większą od 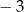
Dwie metalowe kule o promieniach po 2 cm przetopiono z kulami o promieniach 1 cm. Otrzymano jedną kulę o promieniu 3 cm. Ile łącznie kul przetopiono?
A) 11 B) 13 C) 1 D) 3
W autobusie jechało 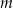 mężczyzn i
mężczyzn i 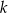 kobiet. Na przystanku wysiedli 2 mężczyźni i 3 kobiety, a wsiadło 5 mężczyzn i 2 kobiety. Gdy autobus odjechał z tego przystanku, podróżowało nim
kobiet. Na przystanku wysiedli 2 mężczyźni i 3 kobiety, a wsiadło 5 mężczyzn i 2 kobiety. Gdy autobus odjechał z tego przystanku, podróżowało nim
A) 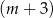 mężczyzn i
mężczyzn i 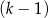 kobiet. B)
kobiet. B) 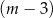 mężczyzn i
mężczyzn i 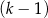 kobiet.
kobiet.
C) 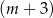 mężczyzn i
mężczyzn i 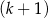 kobiet. D)
kobiet. D) 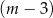 mężczyzn i
mężczyzn i 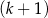 kobiet.
kobiet.
W windzie jechało 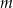 mężczyzn i
mężczyzn i 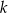 kobiet. Na drugim piętrze wysiadło 3 mężczyzn i 4 kobiety, a wsiadło 2 mężczyzn i 3 kobiety. Gdy winda odjechała z drugiego piętra, znajdowało się w niej
kobiet. Na drugim piętrze wysiadło 3 mężczyzn i 4 kobiety, a wsiadło 2 mężczyzn i 3 kobiety. Gdy winda odjechała z drugiego piętra, znajdowało się w niej
A) 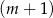 mężczyzn i
mężczyzn i 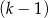 kobiet. B)
kobiet. B) 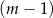 mężczyzn i
mężczyzn i 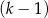 kobiet.
kobiet.
C) 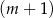 mężczyzn i
mężczyzn i 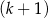 kobiet. D)
kobiet. D) 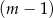 mężczyzn i
mężczyzn i 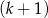 kobiet.
kobiet.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
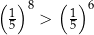 | P | F |
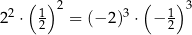 | P | F |
Na trawniku w kształcie kwadratu o boku długości 9 metrów wytyczono kwietnik w kształcie prostokąta tak, że jego boki są równoległe do boków trawnika. Do kwietnika prowadzą cztery ścieżki. Dwie krótsze ścieżki mają po 1,5 m długości każda, a dwie dłuższe mają po 2,5 m długości każda (zobacz rysunek).
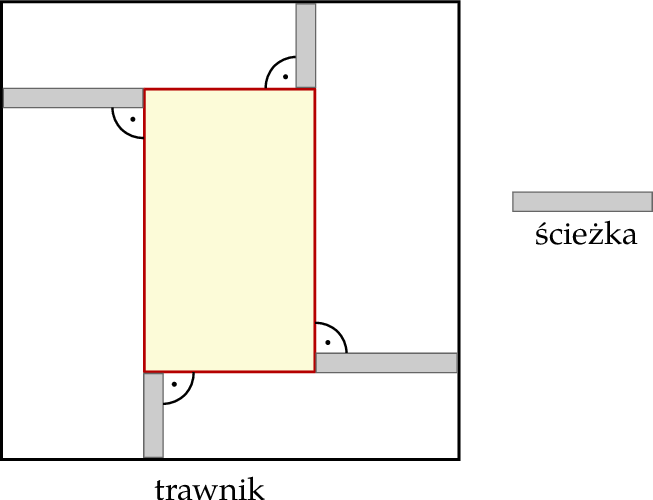
Oblicz pole powierzchni wytyczonego kwietnika.
Ile razy zwiększy się pole koła, jeżeli jego średnica wzrośnie z 2 cm do 6 cm?
Ile razy zwiększy się pole koła, jeżeli jego średnica wzrośnie z 3 cm do 6 cm?
Ile razy zwiększy się pole koła, jeżeli jego średnica wzrośnie z 3 cm do 5 cm?
W pudełku jest 40 kul. Wśród nich jest 35 kul białych, a pozostałe to kule czerwone. Prawdopodobieństwo wylosowania każdej kuli jest takie samo. Z pudełka losujemy jedną kulę. Prawdopodobieństwo zdarzenia polegającego na tym, że otrzymamy kulę czerwoną, jest równe
A)  B)
B) 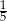 C)
C) 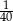 D)
D) 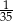
W pudełku jest 60 kul. Wśród nich jest 27 kul białych, 18 kul niebieskich, a pozostałe to kule żółte. Prawdopodobieństwo wylosowania każdej kuli jest takie samo. Z pudełka losujemy jedną kulę. Prawdopodobieństwo zdarzenia polegającego na tym, że otrzymamy kulę, która nie jest niebieska, jest równe
A) 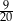 B)
B) 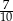 C)
C) 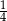 D)
D) 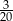
W równoległoboku 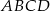 dłuższa podstawa ma długość
dłuższa podstawa ma długość 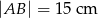 . Wysokości tego równoległoboku mają długości:
. Wysokości tego równoległoboku mają długości: 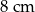 i
i 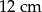 . Zatem krótsza podstawa równoległoboku ma długość
. Zatem krótsza podstawa równoległoboku ma długość
A) 20 cm B) 10 cm C) 3,2 cm D) 1,6 cm
Równoległobok 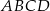 zbudowano z czterech przystających trójkątów prostokątnych (patrz rysunek). Boki równoległoboku mają długości
zbudowano z czterech przystających trójkątów prostokątnych (patrz rysunek). Boki równoległoboku mają długości 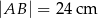 i
i 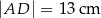 .
.
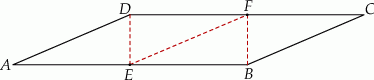
Oblicz pole równoległoboku 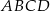 .
.
Równoległobok 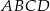 zbudowano z czterech przystających trójkątów prostokątnych (patrz rysunek). Boki równoległoboku mają długości
zbudowano z czterech przystających trójkątów prostokątnych (patrz rysunek). Boki równoległoboku mają długości 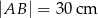 i
i 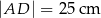 .
.
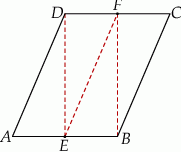
Oblicz pole równoległoboku 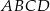 .
.
Poniżej zamieszczono fragment etykiety z sałatki z kurczakiem o masie 250 g.
| Wartość odżywcza | w 100 g |
| energia | 570 kJ/137 kcal |
| tłuszcz w tym kwasy nasycone | 9,5 g 1,6 g |
| węglowodany w tym cukry | 4,6 g 3,3 g |
| błonnik | 2,6 g |
| białko | 7,0 g |
| sól | 0,102 g |
| wapń | 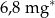 |
| potas | 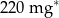 |
 1 mg=0,001 g
1 mg=0,001 g
Zjedzenie całej sałatki dostarcza organizmowi około A/B potasu.
A) 440 mg B) 550 mg
Zjedzenie całej sałatki dostarcza organizmowi C/D razy więcej soli niż wapnia.
C) 15 D) 150
Poniżej zamieszczono fragment etykiety z jogurtu o masie 150 g.
| Wartość odżywcza | w 100 g |
| energia | 290 kJ/69 kcal |
| tłuszcz w tym kwasy nasycone | 3,0 g 1,9 g |
| węglowodany w tym cukry | 5,9 g 5,9 g |
| błonnik | 0 g |
| białko | 4,6 g |
| sól | 0,15 g |
| wapń | 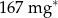 |
| witamina B2 | 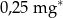 |
 1 mg=0,001 g
1 mg=0,001 g
Zjedzenie całego jogurtu dostarcza organizmowi około A/B wapnia.
A) 167 mg B) 250 mg
Zjedzenie całego jogurtu dostarcza organizmowi C/D razy więcej białka niż witaminy B2.
C) 18,4 D) 18 400
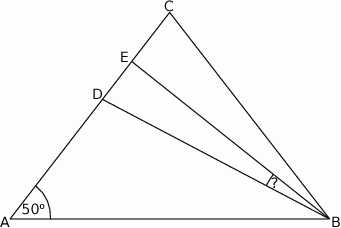
W trójkącie równoramiennym 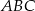 spełnione są warunki:
spełnione są warunki: 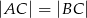 ,
, 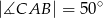 . Odcinek
. Odcinek 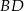 jest dwusieczną kąta
jest dwusieczną kąta 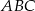 , a odcinek
, a odcinek 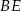 jest wysokością opuszczoną z wierzchołka
jest wysokością opuszczoną z wierzchołka 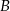 na bok
na bok 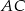 . Miara kąta
. Miara kąta 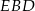 jest równa
jest równa
A) 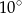 B)
B) 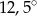 C)
C) 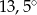 D)
D) 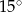
Białystok otrzymał prawa miejskie 448 lat później od Szczecina. W 1915 roku oba miasta obchodziły jubileusz nadania praw miejskich, ale rocznica Szczecina była 3 razy większa od rocznicy Białegostoku. Kiedy te miasta otrzymały prawa miejskie?
Średnia arytmetyczna dwóch liczb wynosi 20. Jeśli jedną z nich zwiększymy dwukrotnie, a drugą zmniejszymy o 50%, to średnia arytmetyczna zwiększy się o 2. Wyznacz te liczby.
Średnia arytmetyczna dwóch liczb wynosi 16. Jeśli jedną z nich zmniejszymy dwukrotnie, a drugą zwiększymy o 50%, to średnia arytmetyczna zwiększy się o 2. Wyznacz te liczby.
Z 24 kwadratów o boku długości 1 zbudowano prostokąt.
Która z podanych liczb nie może być obwodem otrzymanego prostokąta?
A) 20 B) 24 C) 28 D) 50

