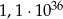Końce odcinka  mają współrzędne
mają współrzędne 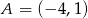 i
i 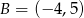 . Na symetralnej odcinka
. Na symetralnej odcinka 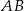 leży punkt o współrzędnych
leży punkt o współrzędnych
A) 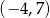 B)
B) 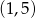 C)
C) 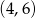 D)
D) 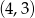
/Szkoła podstawowa
Dany jest zbiór 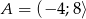 . Do zbioru
. Do zbioru 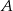 należy
należy
A) 12 liczb całkowitych i 5 liczb pierwszych
B) 13 liczb całkowitych i 9 liczb naturalnych
C) 6 liczb naturalnych i 4 liczby pierwsze
D) 12 liczb całkowitych i 4 liczby pierwsze
Rozwinięcie dziesiętne ułamka 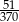 jest równe 0,1(378). Na pięćdziesiątym miejscu po przecinku tego rozwinięcia znajduje się cyfra
jest równe 0,1(378). Na pięćdziesiątym miejscu po przecinku tego rozwinięcia znajduje się cyfra
A) 1 B) 3 C) 7 D) 8
Rozwinięcie dziesiętne ułamka 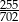 jest równe 0,3(632478). Na czterdziestym miejscu po przecinku tego rozwinięcia znajduje się cyfra
jest równe 0,3(632478). Na czterdziestym miejscu po przecinku tego rozwinięcia znajduje się cyfra
A) 2 B) 4 C) 7 D) 3
Rozwiąż układ równań
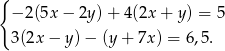
Rozwiąż układ równań 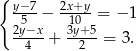
W jakim stosunku można podzielić odcinek o długości 36 cm, aby z otrzymanych czterech odcinków móc zbudować czworokąt?
A) 1 : 1 : 2 : 4 B) 1 : 2 : 2 : 6 C) 2 : 3 : 4 : 8 D) 2 : 3 : 3 : 8
W Polsce olej otrzymuje się głównie z rzepaku i słonecznika. Rzepak zawiera około 40% oleju, natomiast słonecznik około 50%. Z ilu kilogramów rzepaku uzyska się taką samą ilość oleju, co z 260 kg słonecznika?
Wykaż, że odcinek łączący środki dwóch boków trójkąta jest równoległy do trzeciego boku i ma długość równą połowie tego boku.
Sześcian o objętości 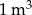 rozcięto na sześciany o krawędzi 1 cm. Gdyby wszystkie otrzymane sześciany ustawiono jeden za drugim, tak jak na rysunku, to powstałby prostopadłościan.
rozcięto na sześciany o krawędzi 1 cm. Gdyby wszystkie otrzymane sześciany ustawiono jeden za drugim, tak jak na rysunku, to powstałby prostopadłościan.
![]()
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Jedna z krawędzi powstałego prostopadłościanu miałaby długość 10 km. | P | F |
| Objętość prostopadłościanu byłaby 100 razy większa od objętości początkowego sześcianu. | P | F |
Z 1 000 000 sześcianów o objętości 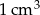 zbudowano prostopadłościan o polu podstawy równym
zbudowano prostopadłościan o polu podstawy równym 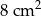 .
.
![]()
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Objętość prostopadłościanu jest równa 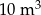 . . | P | F |
| Wysokość prostopadłościanu jest równa 1,25 km. | P | F |
Dane są trzy wyrażenia:
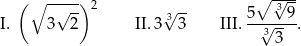
Wartości których wyrażeń są mniejsze od 5?
A) Tylko I i II. B) Tylko I i III. C) Tylko II i III. D) I, II i III.
Dane są trzy wyrażenia:
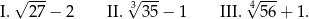
Wartości których wyrażeń są mniejsze od 4?
A) Tylko I i II. B) Tylko I i III. C) Tylko II i III. D) I, II i III.
W trójkącie równobocznym długość każdego boku zmniejszono o 20%. Wtedy pole tego trójkąta
A) zmniejszy się o 20% B) zmniejszy się o 40%
C) zmniejszy się o mniej niż 20% D) zmniejszy się o 36%
Na okręgu o środku 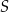 i promieniu
i promieniu 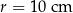 zaznaczono punkty
zaznaczono punkty 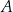 i
i 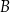 , takie że odcinek
, takie że odcinek 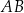 ma długość 16 cm. Następnie dorysowano odcinki
ma długość 16 cm. Następnie dorysowano odcinki 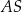 i
i 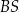 .
.
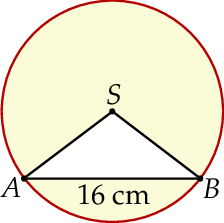
Oblicz pole zacieniowanej figury. W obliczeniach przyjmij 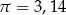 .
.
Zapisz w postaci jednej potęgi liczbę 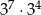 .
.
Zapisz w postaci jednej potęgi liczbę 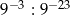 .
.
Zapisz w postaci jednej potęgi liczbę 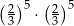 .
.
Zapisz w postaci jednej potęgi liczbę 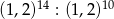 .
.
Zapisz w postaci jednej potęgi liczbę 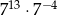 .
.
Zapisz w postaci jednej potęgi liczbę 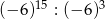 .
.
Zapisz w postaci jednej potęgi liczbę 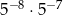 .
.
Zapisz w postaci jednej potęgi liczbę 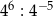 .
.
Wartość wyrażenia 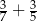 jest liczbą A/B.
jest liczbą A/B.
A) mniejszą od 1 B) większą od 1
Wartość wyrażenia 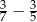 jest liczbą C/D.
jest liczbą C/D.
C) ujemną D) dodatnią
Wartość wyrażenia 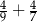 jest liczbą A/B.
jest liczbą A/B.
A) mniejszą od 1 B) większą od 1
Wartość wyrażenia 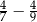 jest liczbą C/D.
jest liczbą C/D.
C) ujemną D) dodatnią
Poniżej zapisano trzy liczby:
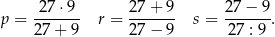
Który zapis przedstawia poprawnie uporządkowane liczby 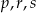 od najmniejszej do największej?
od najmniejszej do największej?
A) 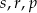 B)
B) 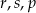 C)
C) 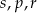 D)
D) 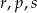
Poniżej zapisano trzy liczby:
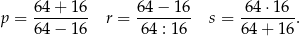
Który zapis przedstawia poprawnie uporządkowane liczby 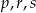 od największej do najmniejszej?
od największej do najmniejszej?
A) 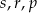 B)
B) 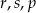 C)
C) 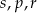 D)
D) 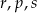
Dwie spośród liczb 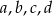 są dodatnie, a dwie ujemne.
są dodatnie, a dwie ujemne.
Ile najwięcej liczb ujemnych może być pośród liczb 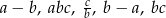 ?
?
A) Dwie. B) Trzy. C) Cztery. D) Pięć.
Prostopadłościenne paczki wysyłane za pośrednictwem firmy kurierskiej dzielone są na 5 kategorii w zależności od rozmiarów paczki.

| Kategoria | najdłuższy bok + najkrótszy bok |
| XS | 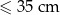 |
| S | 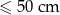 |
| M | 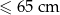 |
| L | 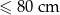 |
| XL | 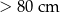 |
Do podanych wymiarów paczek dopisz odpowiadającą im kategorię.
| Wymiary | Kategoria |
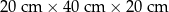 | |
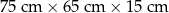 |
Równoległobok 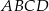 o bokach długości 6 cm i 9 cm rozcięto wzdłuż prostej
o bokach długości 6 cm i 9 cm rozcięto wzdłuż prostej  na dwa trapezy tak, jak pokazano na rysunku. Odcinek
na dwa trapezy tak, jak pokazano na rysunku. Odcinek 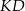 ma długość 4,8 cm.
ma długość 4,8 cm.
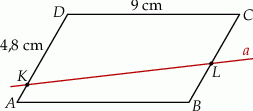
Pole trapezu 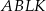 jest trzykrotnie mniejsze od pola równoległoboku
jest trzykrotnie mniejsze od pola równoległoboku 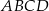 . Oblicz długość odcinka
. Oblicz długość odcinka 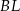 . Zapisz obliczenia.
. Zapisz obliczenia.
Pola dwóch trójkątów równobocznych są równe odpowiednio 7 i 63.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Obwód drugiego trójkąta jest 9 razy większy od obwodu pierwszego trójkąta. | P | F |
Pierwszy trójkąt jest podobny do drugiego w skali 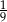 | P | F |
Rozwiązaniem równania
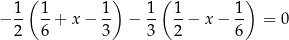
jest liczba
A) 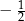 B)
B) 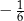 C)
C) 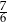 D)
D) 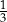 E)
E) 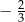
Sześcian o krawędzi długości 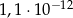 ma objętość równą
ma objętość równą
A) 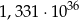 B)
B) 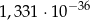 C)
C) 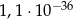 D)
D)