Które z dwóch podanych liczb mają tę własność, że ich suma jest równa ich iloczynowi?
A) 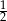 i
i 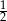 B)
B) 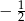 i 1. C)
i 1. C) 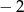 i
i 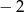 D)
D) 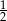 i
i 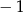
/Szkoła podstawowa
Rozważmy treść następującego zadania:
Obwód rombu o przekątnych długości  i
i 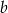 jest równy 48. Pole tego rombu jest równe 16. Oblicz długości przekątnych tego rombu.
jest równy 48. Pole tego rombu jest równe 16. Oblicz długości przekątnych tego rombu.
Który układ równań opisuje zależności między długościami przekątnych tego rombu?
A) 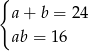 B)
B) 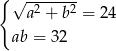 C)
C) 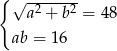 D)
D) 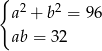
Samochód pana Jana spala w jeździe miejskiej 10,3 l benzyny na 100 km, a poza miastem 7,2 l na 100 km. Pan Jan wybrał się w podróż do miejscowości oddalonej od jego domu o 600 km. Aby wyjechać z miasta, musi pokonać 32 km. Czy wystarczy mu benzyny, jeżeli zatankuje 47-litrowy bak do pełna? Ile benzyny mu zostanie lub zabraknie? Wynik podaj z dokładnością do 0,1 litra.
Jeden z kątów wewnętrznych trójkąta ma miarę  , drugi ma miarę o
, drugi ma miarę o 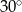 większą niż kąt
większą niż kąt  , a trzeci ma miarę trzy razy większą niż kąt
, a trzeci ma miarę trzy razy większą niż kąt  . Trójkąt ten jest
. Trójkąt ten jest
A) równoboczny. B) równoramienny. C) rozwartokątny. D) prostokątny.
Jeden z kątów wewnętrznych trójkąta ma miarę  , drugi ma miarę o
, drugi ma miarę o 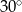 większą niż kąt
większą niż kąt  , a trzeci ma miarę cztery razy większą niż kąt
, a trzeci ma miarę cztery razy większą niż kąt  . Trójkąt ten jest
. Trójkąt ten jest
A) równoboczny. B) równoramienny. C) rozwartokątny. D) prostokątny.
Jeden z kątów wewnętrznych trójkąta ma miarę  , drugi ma miarę o
, drugi ma miarę o 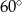 większą niż kąt
większą niż kąt  , a trzeci ma miarę cztery razy większą niż kąt
, a trzeci ma miarę cztery razy większą niż kąt  .
.
Trójkąt ten jest
A) równoboczny. B) równoramienny. C) rozwartokątny. D) prostokątny.
Wykres przedstawia liczbę pasażerów w autobusie w trakcie kolejnych kursów.
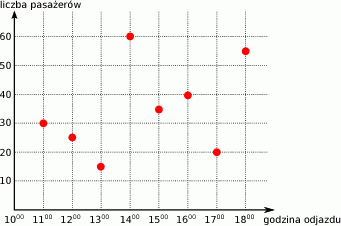
Ilu pasażerów jechało autobusem o godzinie 14:00?
A) 20 B) 40 C) 50 D) 60
Wykres przedstawia liczbę pasażerów w autobusie w trakcie kolejnych kursów.
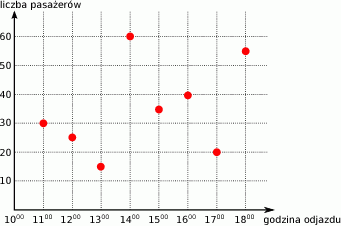
O ilu więcej pasażerów jechało o 16:00 niż o 12:00?
A) o 5 B) o 20 C) o 10 D) o 15
Wykres przedstawia liczbę pasażerów w autobusie w trakcie kolejnych kursów.
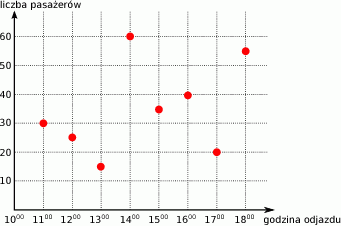
O której godzinie w autobusie było 15 pasażerów?
A) o 13:00 B) o 14:00 C) o 17:00 D) o żadnej
Wykres przedstawia liczbę pasażerów w autobusie w trakcie kolejnych kursów.
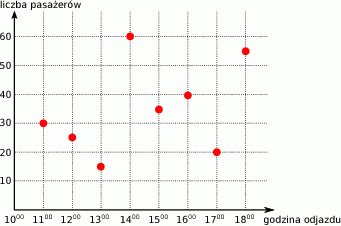
Ile razy więcej pasażerów jechało autobusem o 16:00, niż o 17:00?
A) 20 razy B) 2 razy C) 1,5 raza D) nie można tego obliczyć
Ada wycięła z kartonu równoległobok  o bokach
o bokach 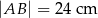 ,
, 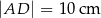 i polu równym
i polu równym 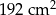 (rysunek I). Następnie rozcięła ten równoległobok na dwie pary przystających trapezów i złożyła z tych trapezów wielokąt przedstawiony na rysunku II. Od tego wielokąta odcięła dolną część wzdłuż jego przekątnej
(rysunek I). Następnie rozcięła ten równoległobok na dwie pary przystających trapezów i złożyła z tych trapezów wielokąt przedstawiony na rysunku II. Od tego wielokąta odcięła dolną część wzdłuż jego przekątnej 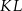 i otrzymała w ten sposób wielokąt przedstawiony na rysunku III.
i otrzymała w ten sposób wielokąt przedstawiony na rysunku III.
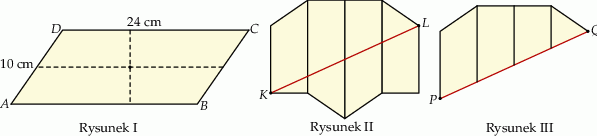
Oblicz obwód wielokąta z rysunku III.
Grupa motocyklistów w ciągu czterech dni pokonała dystans 221 km, przy czym liczby pokonanych kilometrów w kolejnych dniach są do siebie w proporcji 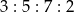 . Oblicz ile kilometrów motocykliści pokonywali w kolejnych dniach.
. Oblicz ile kilometrów motocykliści pokonywali w kolejnych dniach.
Punkty 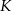 ,
, 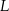 i
i 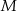 są środkami boków
są środkami boków 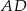 ,
, 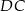 i
i 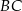 kwadratu
kwadratu 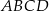 (rysunek).
(rysunek).
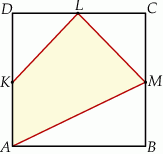
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole trójkąta 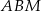 stanowi stanowi 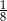 pola kwadratu pola kwadratu 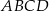 . . | P | F |
Pole czworokąta 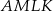 stanowi połowę pola kwadratu stanowi połowę pola kwadratu 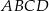 . . | P | F |
Narysowany kwadrat należy wypełnić tak, aby iloczyny liczb w każdym wierszu, każdej kolumnie i na obu przekątnych kwadratu były takie same.

Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Iloczyn liczb na przekątnej kwadratu jest równy 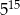 . . | P | F |
W zacieniowane pole kwadratu należy wpisać liczbę 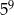 . . | P | F |
Narysowany kwadrat należy wypełnić tak, aby iloczyny liczb w każdym wierszu, każdej kolumnie i na obu przekątnych kwadratu były takie same.

Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Iloczyn wszystkich liczb w kwadracie jest równy 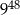 . . | P | F |
W zacieniowane pole kwadratu należy wpisać liczbę 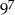 . . | P | F |
Liczba 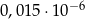 jest równa
jest równa
A) 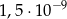 B)
B) 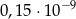 C)
C) 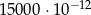 D) 0,0000015
D) 0,0000015
Liczba 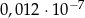 jest równa
jest równa
A) 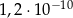 B)
B) 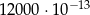 C)
C) 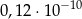 D) 0,00000012
D) 0,00000012
Kąt środkowy oparty na łuku okręgu długości 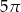 ma miarę
ma miarę 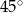 . Pole koła ograniczonego tym okręgiem jest równe
. Pole koła ograniczonego tym okręgiem jest równe
A) 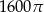 B)
B) 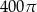 C)
C) 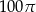 D)
D) 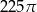
Punkt 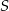 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 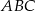 , a punkty
, a punkty 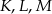 są punktami styczności tego okręgu z bokami trójkąta. Odcinek
są punktami styczności tego okręgu z bokami trójkąta. Odcinek 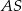 ma długość 26 cm, a odcinek
ma długość 26 cm, a odcinek 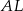 ma długość 24 cm.
ma długość 24 cm.
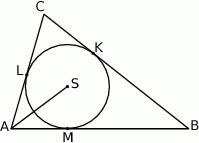
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Promień okręgu wpisanego w trójkąt 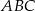 jest równy 9 cm. jest równy 9 cm. | P | F |
Odcinki 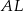 i i 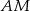 mają tę samą długość. mają tę samą długość. | P | F |
Córka obecnie jest 4 razy młodsza od swojej mamy. Razem mają 60 lat. Mama obecnie ma A/B lat.
A) 48 B) 45
Córka za 8 lat będzie miała C/D.
C) 23 lata D) 20 lat
Córka obecnie jest 3 razy młodsza od swojej mamy. Razem mają 64 lata. Mama obecnie ma A/B lat.
A) 48 B) 45
Córka za 8 lat będzie miała C/D.
C) 24 lata D) 20 lat
Liczba 129 500 000 zapisana w notacji wykładniczej to
A) 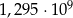 B)
B) 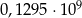 C)
C) 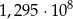 D)
D) 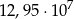
Dostęp do pliku jest chroniony hasłem 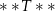 złożonym z dwóch liczb dwucyfrowych oddzielonych literą
złożonym z dwóch liczb dwucyfrowych oddzielonych literą 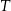 . Pierwsza liczba hasła to sześcian liczby 4, a druga to najmniejszy wspólny mianownik ułamków
. Pierwsza liczba hasła to sześcian liczby 4, a druga to najmniejszy wspólny mianownik ułamków 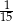 i
i 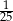 . Jakie jest hasło do pliku?
. Jakie jest hasło do pliku?
A) 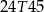 B)
B) 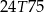 C)
C) 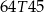 D)
D) 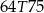
Dostęp do pliku jest chroniony hasłem 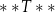 złożonym z dwóch liczb dwucyfrowych oddzielonych literą
złożonym z dwóch liczb dwucyfrowych oddzielonych literą 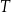 . Pierwsza liczba hasła to najmniejszy wspólny mianownik ułamków
. Pierwsza liczba hasła to najmniejszy wspólny mianownik ułamków 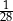 i
i 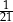 , a druga to reszta z dzielenia pierwszej liczby przez 29. Jakie jest hasło do pliku?
, a druga to reszta z dzielenia pierwszej liczby przez 29. Jakie jest hasło do pliku?
A) 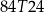 B)
B) 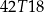 C)
C) 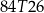 D)
D) 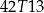
Przekątna kwadratu 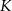 ma długość 2, a obwód kwadratu
ma długość 2, a obwód kwadratu 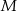 ma długość 16. Skala podobieństwa kwadratu
ma długość 16. Skala podobieństwa kwadratu 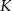 do kwadratu
do kwadratu 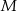 jest równa:
jest równa:
A) 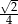 B)
B) 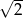 C) 4 D)
C) 4 D) 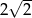
Wymień liczby naturalne większe od 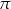 i mniejsze od
i mniejsze od 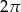 .
.
Wymień ujemne liczby całkowite większe od 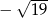
Sześć różnych liczb naturalnych zapisano w kolejności od najmniejszej do największej:
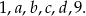
Mediana liczb: 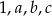 jest dwa razy mniejsza od mediany liczb
jest dwa razy mniejsza od mediany liczb 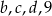 , a średnia arytmetyczna liczb
, a średnia arytmetyczna liczb 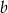 i
i  jest liczbą naturalną. Mediana liczb
jest liczbą naturalną. Mediana liczb 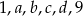 jest równa
jest równa
A) 5 B) 4 C) 6 D) 3
Oblicz pole i obwód równoległoboku przedstawionego na rysunku.
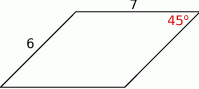
Oblicz pole i obwód równoległoboku przedstawionego na rysunku.
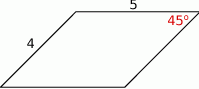
Oblicz pole i obwód równoległoboku przedstawionego na rysunku.
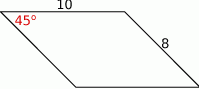
Dane jest przybliżenie 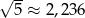 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
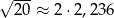 | P | F |
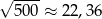 | P | F |
Dane jest przybliżenie 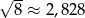 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
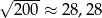 | P | F |
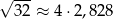 | P | F |

