Punkty 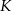 ,
, 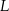 i
i 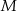 są środkami boków
są środkami boków 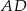 ,
, 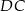 i
i 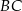 kwadratu
kwadratu 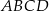 (rysunek).
(rysunek).
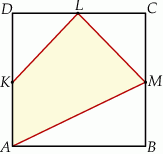
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole trójkąta 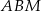 stanowi stanowi 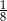 pola kwadratu pola kwadratu 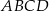 . . | P | F |
Pole czworokąta 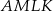 stanowi połowę pola kwadratu stanowi połowę pola kwadratu 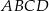 . . | P | F |
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Punkty 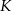 ,
, 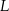 i
i 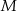 są środkami boków
są środkami boków 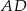 ,
, 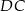 i
i 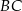 kwadratu
kwadratu 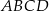 (rysunek).
(rysunek).

Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole trójkąta 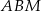 stanowi stanowi 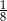 pola kwadratu pola kwadratu  . . | P | F |
Pole czworokąta 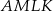 stanowi połowę pola kwadratu stanowi połowę pola kwadratu 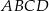 . . | P | F |
Narysowany kwadrat należy wypełnić tak, aby iloczyny liczb w każdym wierszu, każdej kolumnie i na obu przekątnych kwadratu były takie same.

Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Iloczyn liczb na przekątnej kwadratu jest równy 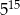 . . | P | F |
W zacieniowane pole kwadratu należy wpisać liczbę 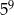 . . | P | F |
Narysowany kwadrat należy wypełnić tak, aby iloczyny liczb w każdym wierszu, każdej kolumnie i na obu przekątnych kwadratu były takie same.

Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Iloczyn wszystkich liczb w kwadracie jest równy 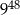 . . | P | F |
W zacieniowane pole kwadratu należy wpisać liczbę 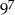 . . | P | F |
Liczba 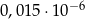 jest równa
jest równa
A) 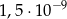 B)
B) 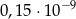 C)
C) 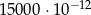 D) 0,0000015
D) 0,0000015
Liczba 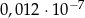 jest równa
jest równa
A) 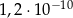 B)
B) 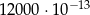 C)
C) 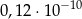 D) 0,00000012
D) 0,00000012
Kąt środkowy oparty na łuku okręgu długości 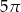 ma miarę
ma miarę 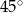 . Pole koła ograniczonego tym okręgiem jest równe
. Pole koła ograniczonego tym okręgiem jest równe
A) 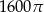 B)
B) 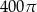 C)
C) 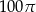 D)
D) 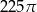
Punkt 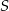 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 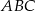 , a punkty
, a punkty 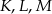 są punktami styczności tego okręgu z bokami trójkąta. Odcinek
są punktami styczności tego okręgu z bokami trójkąta. Odcinek 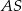 ma długość 26 cm, a odcinek
ma długość 26 cm, a odcinek 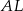 ma długość 24 cm.
ma długość 24 cm.
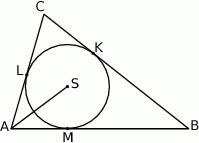
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Promień okręgu wpisanego w trójkąt 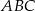 jest równy 9 cm. jest równy 9 cm. | P | F |
Odcinki 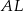 i i 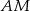 mają tę samą długość. mają tę samą długość. | P | F |
Córka obecnie jest 4 razy młodsza od swojej mamy. Razem mają 60 lat. Mama obecnie ma A/B lat.
A) 48 B) 45
Córka za 8 lat będzie miała C/D.
C) 23 lata D) 20 lat
Córka obecnie jest 3 razy młodsza od swojej mamy. Razem mają 64 lata. Mama obecnie ma A/B lat.
A) 48 B) 45
Córka za 8 lat będzie miała C/D.
C) 24 lata D) 20 lat
Liczba 129 500 000 zapisana w notacji wykładniczej to
A) 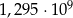 B)
B) 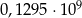 C)
C) 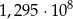 D)
D) 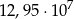
Dostęp do pliku jest chroniony hasłem 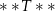 złożonym z dwóch liczb dwucyfrowych oddzielonych literą
złożonym z dwóch liczb dwucyfrowych oddzielonych literą 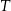 . Pierwsza liczba hasła to sześcian liczby 4, a druga to najmniejszy wspólny mianownik ułamków
. Pierwsza liczba hasła to sześcian liczby 4, a druga to najmniejszy wspólny mianownik ułamków 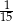 i
i 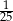 . Jakie jest hasło do pliku?
. Jakie jest hasło do pliku?
A) 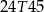 B)
B) 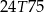 C)
C) 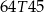 D)
D) 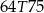
Dostęp do pliku jest chroniony hasłem 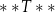 złożonym z dwóch liczb dwucyfrowych oddzielonych literą
złożonym z dwóch liczb dwucyfrowych oddzielonych literą 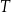 . Pierwsza liczba hasła to najmniejszy wspólny mianownik ułamków
. Pierwsza liczba hasła to najmniejszy wspólny mianownik ułamków 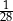 i
i 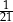 , a druga to reszta z dzielenia pierwszej liczby przez 29. Jakie jest hasło do pliku?
, a druga to reszta z dzielenia pierwszej liczby przez 29. Jakie jest hasło do pliku?
A) 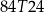 B)
B) 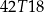 C)
C) 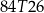 D)
D) 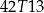
Przekątna kwadratu 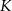 ma długość 2, a obwód kwadratu
ma długość 2, a obwód kwadratu 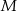 ma długość 16. Skala podobieństwa kwadratu
ma długość 16. Skala podobieństwa kwadratu 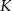 do kwadratu
do kwadratu 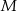 jest równa:
jest równa:
A) 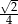 B)
B) 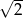 C) 4 D)
C) 4 D) 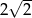
Wymień liczby naturalne większe od 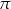 i mniejsze od
i mniejsze od 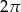 .
.
Wymień ujemne liczby całkowite większe od 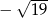
Sześć różnych liczb naturalnych zapisano w kolejności od najmniejszej do największej:
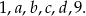
Mediana liczb: 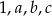 jest dwa razy mniejsza od mediany liczb
jest dwa razy mniejsza od mediany liczb 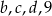 , a średnia arytmetyczna liczb
, a średnia arytmetyczna liczb 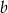 i
i  jest liczbą naturalną. Mediana liczb
jest liczbą naturalną. Mediana liczb 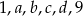 jest równa
jest równa
A) 5 B) 4 C) 6 D) 3
Oblicz pole i obwód równoległoboku przedstawionego na rysunku.
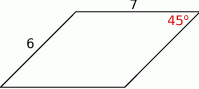
Oblicz pole i obwód równoległoboku przedstawionego na rysunku.
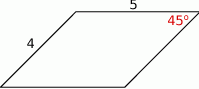
Oblicz pole i obwód równoległoboku przedstawionego na rysunku.
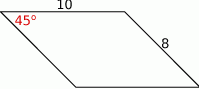
Dane jest przybliżenie 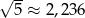 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
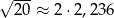 | P | F |
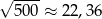 | P | F |
Dane jest przybliżenie 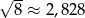 . Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
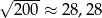 | P | F |
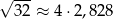 | P | F |
Z jednakowych sześciennych kostek, których krawędź ma długość 1, sklejono bryłę przedstawioną na rysunku.
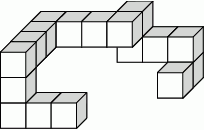
Ile kostek należy dokleić do tej bryły, aby otrzymać wypełniony kostkami sześcian?
Rzucono 100 razy sześcienną kostką do gry. Średnia arytmetyczna liczb oczek w pierwszych 40 rzutach była równa 3,75, a średnia arytmetyczna liczb oczek w kolejnych 60 rzutach była równa 4,25. Średnia arytmetyczna liczb oczek w 100 rzutach jest
A) mniejsza od 4 B) równa 4 C) równa 4,05 D) większa od 4,05
Trójki liczb naturalnych 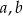 i
i  , które spełniają warunek
, które spełniają warunek 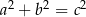 , nazywamy trójkami pitagorejskimi. Niektóre z nich znajdujemy z wykorzystaniem wzorów:
, nazywamy trójkami pitagorejskimi. Niektóre z nich znajdujemy z wykorzystaniem wzorów:
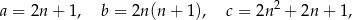
gdzie  oznacza dowolną liczbę naturalną (
oznacza dowolną liczbę naturalną (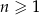 ).
).
Liczba  zawsze będzie A/B.
zawsze będzie A/B.
A) parzysta B) nieparzysta
Liczby 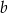 i
i  różnią się o C/D.
różnią się o C/D.
C) 1 D) 
Trójki liczb naturalnych 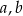 i
i  , które spełniają warunek
, które spełniają warunek 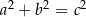 , nazywamy trójkami pitagorejskimi. Niektóre z nich znajdujemy z wykorzystaniem wzorów:
, nazywamy trójkami pitagorejskimi. Niektóre z nich znajdujemy z wykorzystaniem wzorów:
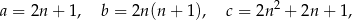
gdzie  oznacza dowolną liczbę naturalną (
oznacza dowolną liczbę naturalną (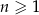 ).
).
Jeżeli najmniejsza z liczb 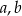 i
i  jest równa 11, to największa z tych liczb jest równa
jest równa 11, to największa z tych liczb jest równa
A) 265 B) 73 C) 145 D) 61
Trójki liczb naturalnych 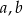 i
i  , które spełniają warunek
, które spełniają warunek 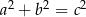 , nazywamy trójkami pitagorejskimi. Niektóre z nich znajdujemy z wykorzystaniem wzorów:
, nazywamy trójkami pitagorejskimi. Niektóre z nich znajdujemy z wykorzystaniem wzorów:
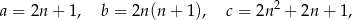
gdzie  oznacza dowolną liczbę naturalną (
oznacza dowolną liczbę naturalną (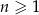 ).
).
Liczba 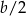 zawsze będzie A/B.
zawsze będzie A/B.
A) parzysta B) nieparzysta
Liczby 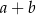 i
i  różnią się o C/D.
różnią się o C/D.
C) 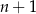 D)
D) 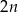
Trójki liczb naturalnych 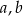 i
i  , które spełniają warunek
, które spełniają warunek 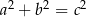 , nazywamy trójkami pitagorejskimi. Niektóre z nich znajdujemy z wykorzystaniem wzorów:
, nazywamy trójkami pitagorejskimi. Niektóre z nich znajdujemy z wykorzystaniem wzorów:
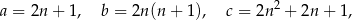
gdzie  oznacza dowolną liczbę naturalną (
oznacza dowolną liczbę naturalną (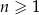 ).
).
Jeżeli najmniejsza z liczb 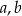 i
i  jest równa 9, to największa z tych liczb jest równa
jest równa 9, to największa z tych liczb jest równa
A) 41 B) 73 C) 145 D) 181
Tata Bartka przed wyjazdem z Krakowa do Warszawy analizuje niektóre bezpośrednie połączenia między tymi miastami. Do wyboru ma cztery połączenia przedstawione w poniższej tabeli.
| Godzina wyjazdu z Krakowa | Godzina przyjazdu do Warszawy | Środek transportu | Długość trasy | Cena biletu |
| 1:35 | 6:30 | autobus | 298 km | 27 zł |
| 2:32 | 5:12 | pociąg | 293 km | 60 zł |
| 5:00 | 8:48 | pociąg | 364 km | 65 zł |
| 5:53 | 8:10 | pociąg | 293 km | 49 zł |
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Za przejazd w najkrótszym czasie należy zapłacić 49 zł. | P | F |
| Zgodnie z rozkładem jazdy tylko przejazd autobusem trwa dłużej niż 4 godziny. | P | F |
Tata Kamila przed wyjazdem z Warszawy do Krakowa analizuje niektóre bezpośrednie połączenia między tymi miastami. Do wyboru ma cztery połączenia przedstawione w poniższej tabeli.
| Godzina wyjazdu z Warszawy | Godzina przyjazdu do Krakowa | Środek transportu | Długość trasy | Cena biletu |
| 1:35 | 6:30 | autobus | 298 km | 27 zł |
| 2:32 | 5:12 | pociąg | 293 km | 60 zł |
| 4:36 | 8:48 | pociąg | 364 km | 58 zł |
| 5:53 | 8:10 | pociąg | 293 km | 65 zł |
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Za przejazd w najkrótszym czasie należy zapłacić 65 zł. | P | F |
| Zgodnie z rozkładem jazdy tylko przejazd autobusem trwa dłużej niż 4 godziny. | P | F |
Na boku 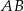 trójkąta
trójkąta 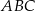 znajduje się taki punkt
znajduje się taki punkt 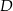 , że
, że 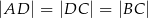 . Miara kąta
. Miara kąta 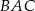 jest równa
jest równa 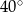 .
.
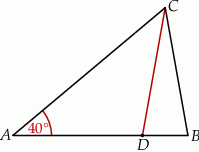
Uzasadnij, że miara kąta 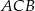 jest trzy większa od miary kąta
jest trzy większa od miary kąta 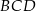 .
.
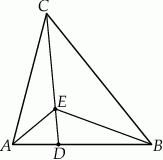
Na boku 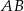 trójkąta
trójkąta 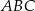 wybrano punkt
wybrano punkt 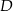 , a na odcinku
, a na odcinku 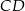 wybrano punkt
wybrano punkt 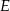 . Wykaż, że stosunek pól trójkątów
. Wykaż, że stosunek pól trójkątów 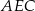 i
i 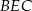 jest równy stosunkowi pól trójkątów
jest równy stosunkowi pól trójkątów 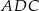 i
i 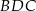 .
.
Kolarz przejechał 4 km ze średnią prędkością 16 km/h, a następnie 9 km ze średnią prędkością 12 km/h. Oblicz z jaką średnią prędkością jechał kolarz na całej trasie.
