Liczba  jest nieparzystą liczbą dwucyfrową, która jest jednocześnie sześcianem liczby naturalnej. Liczba
jest nieparzystą liczbą dwucyfrową, która jest jednocześnie sześcianem liczby naturalnej. Liczba 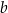 jest dwucyfrową liczbą podzielną przez 12, która jest jednocześnie kwadratem liczby naturalnej. Różnica
jest dwucyfrową liczbą podzielną przez 12, która jest jednocześnie kwadratem liczby naturalnej. Różnica 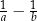 jest równa
jest równa
A) 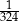 B)
B) 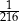 C)
C) 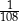 D)
D) 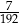
/Szkoła podstawowa
Adam mieszka w miejscowości Bocianowo, a jego kolega Bartek – w miejscowości Żabno. Adam umówił się z Bartkiem w Żabnie na godzinę 18:00. Wyjechał z Bocianowa na skuterze o godzinie 17:20. Średnia prędkość jazdy Adama była równa 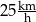 . Na kwadratowej siatce Adam przedstawił schemat trasy, którą jechał.
. Na kwadratowej siatce Adam przedstawił schemat trasy, którą jechał.
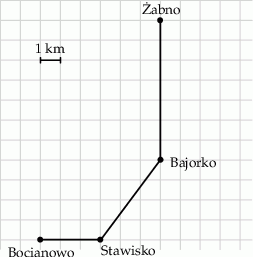
O której godzinie Adam dotarł na spotkanie z Bartkiem?
Ela mieszka w miejscowości Zalesie, a jej koleżanka Kasia – w miejscowości Podgaj. Ela umówiła się z Kasią w Podgaju na godzinę 14:00. Wyjechała z Zalesia na skuterze o godzinie 13:10. Średnia prędkość jazdy Eli była równa 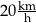 . Na kwadratowej siatce Ela przedstawiła schemat trasy, którą jechała.
. Na kwadratowej siatce Ela przedstawiła schemat trasy, którą jechała.

O której godzinie Ela dotarła na spotkanie z Kasią?
Dane są dwie liczby: 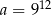 i
i 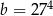 .
.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Iloczyn 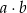 jest równy jest równy 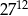 . . | P | F |
Iloraz 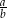 jest równy jest równy 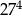 . . | P | F |
Środkowa 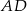 trójkąta
trójkąta 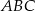 ma długość równą połowie długości boku
ma długość równą połowie długości boku 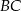 oraz
oraz 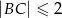 . Wykaż, że
. Wykaż, że 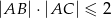 .
.
Wyznacz niewiadomą 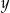 z równania
z równania 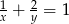 , gdzie
, gdzie 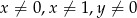 .
.
Wyznacz 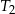 ze wzoru
ze wzoru 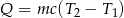 .
.
Medianą danych 2,3,3,4,6,7,7,7 jest liczba
A) 4 B) 5 C) 6 D) 7
Medianą danych 2,3,4,5,7,7,7,9 jest liczba
A) 4 B) 5 C) 6 D) 7
Medianą danych 2,3,3,3,5,7,8,9 jest liczba
A) 4 B) 5 C) 6 D) 7
Medianą danych 1,2,3,5,7,7,8,9 jest liczba
A) 4 B) 5 C) 6 D) 7
Różnica miar kątów wewnętrznych przy ramieniu trapezu równoramiennego, który nie jest równoległobokiem, jest równa 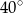 . Miara kąta przy krótszej podstawie tego trapezu jest równa
. Miara kąta przy krótszej podstawie tego trapezu jest równa
A) 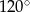 B)
B) 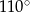 C)
C) 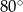 D)
D) 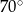
Różnica miar kątów wewnętrznych przy ramieniu trapezu równoramiennego, który nie jest równoległobokiem, jest równa 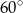 . Miara kąta przy krótszej podstawie tego trapezu jest równa
. Miara kąta przy krótszej podstawie tego trapezu jest równa
A) 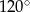 B)
B) 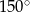 C)
C) 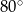 D)
D) 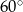
Różnica miar kątów wewnętrznych przy ramieniu trapezu równoramiennego, który nie jest równoległobokiem, jest równa 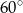 . Miara kąta przy krótszej podstawie tego trapezu jest równa
. Miara kąta przy krótszej podstawie tego trapezu jest równa
A) 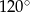 B)
B) 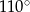 C)
C) 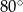 D)
D) 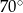
Na osi liczbowej zaznaczono dwa punkty opisane wyrażeniami algebraicznymi.
![]()
Wyrażenie opisujące odległość tych punktów na osi liczbowej jest równe
A) 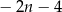 B)
B) 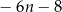 C)
C) 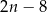 D)
D) 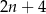
Wykres funkcji liniowej 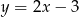 przecina oś
przecina oś 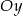 w punkcie o współrzędnych
w punkcie o współrzędnych
A) 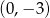 B)
B) 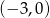 C)
C) 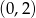 D)
D) 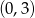
Wykres funkcji liniowej 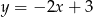 przecina oś
przecina oś 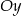 w punkcie o współrzędnych
w punkcie o współrzędnych
A) 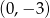 B)
B) 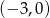 C)
C) 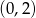 D)
D) 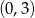
Wiedząc, że boki trójkąta prostokątnego mają długości: 20, 15, 25, wyznacz długość wysokości opuszczonej na przeciwprostokątną.
Boki trójkąta prostokątnego mają długości 10,24,26. Oblicz długość wysokości opuszczonej na przeciwprostokątną.
Mediana kolejnych pięciu liczb naturalnych jest równa 7. Najmniejsza z tych liczb to
A) 5 B) 9 C) 8 D) 11
Mediana kolejnych pięciu liczb naturalnych jest równa 8. Najmniejsza z tych liczb to
A) 9 B) 10 C) 6 D) 12
Mediana kolejnych pięciu liczb naturalnych jest równa 12. Najmniejsza z tych liczb to
A) 16 B) 14 C) 13 D) 10
Mediana kolejnych sześciu liczb naturalnych jest równa 47,5. Najmniejsza z tych liczb to
A) 46 B) 41 C) 45 D) 44
Zapisz wzór i narysuj wykres funkcji, która każdej liczbie przyporządkowuje liczbę o 2 większą od połowy tej liczby.
Różnica miar dwóch kątów rozwartych trapezu jest równa 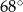 . Dodatnia różnica miar kątów ostrych tego trapezu jest więc równa
. Dodatnia różnica miar kątów ostrych tego trapezu jest więc równa
A) 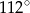 B)
B) 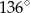 C)
C) 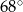 D)
D) 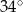
Odczytaj z wykresu, dla jakich argumentów funkcja rośnie, a dla jakich maleje.
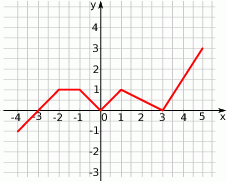
Odczytaj z wykresu, dla jakich argumentów funkcja rośnie, a dla jakich maleje.
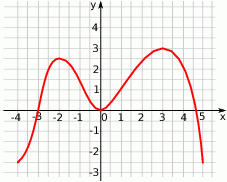
Na rysunku przedstawiono oś liczbową, na której kropkami zaznaczono cztery liczby.
![]()
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Iloczyn dwóch spośród zaznaczonych liczb jest równy iloczynowi dwóch pozostałych. | P | F |
| Suma dwóch spośród zaznaczonych liczb jest równa sumie dwóch pozostałych. | P | F |
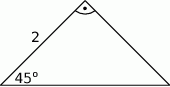
Oblicz pole trójkąta przedstawionego na rysunku.
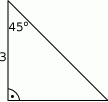
Oblicz pole trójkąta przedstawionego na rysunku.
Hania pokonuje drogę 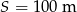 z domu do szkoły w czasie 30 min. Z jaką średnią prędkością idzie Hania?
z domu do szkoły w czasie 30 min. Z jaką średnią prędkością idzie Hania?
A) 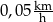 B)
B) 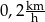 C)
C) 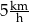 D)
D) 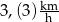
Sonda Voyager 2, która została wysłana w przestrzeń kosmiczną w 1977 roku, w 2007 roku znalazła się na granicy heliosfery w odległości 17,5 bilionów kilometrów od słońca. Od tej pory sonda oddala się od słońca ze stałą prędkością równą 15,35 km/s. Prędkość sondy Voyager 2 po opuszczeniu heliosfery jest równa
A) 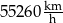 B)
B) 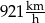 C)
C) 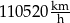 D)
D) 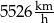
Kasia przejechała na rowerze trasę długości 900 m w czasie 3 min. Prędkość średnia, jaką uzyskała Kasia na tej trasie, jest równa
A) 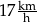 B)
B) 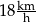 C)
C) 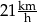 D)
D) 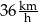
Paweł przejechał na rowerze trasę długości 700 m w czasie 2 min. Prędkość średnia, jaką uzyskał Paweł na tej trasie, jest równa
A) 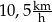 B)
B) 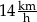 C)
C) 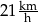 D)
D) 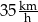
Samochód przejechał ze stałą prędkością trasę o długości 18 kilometrów w czasie 12 minut. Samochód przejechał tę trasę z prędkością
A) 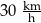 B)
B) 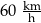 C)
C) 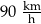 D)
D) 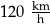
Jeżeli kilogram ziemniaków kosztuje  złotych, a 5 kilogramów ziemniaków kosztuje
złotych, a 5 kilogramów ziemniaków kosztuje 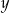 złotych, to
złotych, to
A) 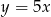 B)
B) 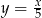 C)
C) 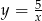 D)
D) 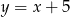
Jeżeli kilogram ziemniaków kosztuje  złotych, a za 5 zł kupiono
złotych, a za 5 zł kupiono 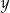 kg ziemniaków, to
kg ziemniaków, to
A) 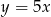 B)
B) 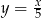 C)
C) 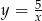 D)
D) 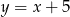
Koncern paliwowy podnosił dwukrotnie w jednym tygodniu cenę benzyny, pierwszy raz o 10%, a drugi raz o 5%. Po obu tych podwyżkach jeden litr benzyny, wyprodukowanej przez ten koncern, kosztuje 4,62 zł. Oblicz cenę jednego litra benzyny przed omawianymi podwyżkami.
W poniedziałek cenę pewnego towaru zwiększono o 10%, zaś w środę zmniejszono o 15%. Oblicz początkową cenę tego towaru, jeśli ostatecznie po tych zmianach wynosiła 187 zł.
W poniedziałek cenę pewnego towaru zmniejszono o 10%, zaś w środę zwiększono o 20%. Oblicz początkową cenę tego towaru, jeśli ostatecznie po tych zmianach wynosiła 324 zł.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| W pięciu rzutach standardową sześcienną kostką do gry, jeżeli wynik każdego rzutu będzie inny, można otrzymać łącznie dokładnie 20 oczek. | P | F |
| W 16 rzutach standardową sześcienną kostką do gry można otrzymać łącznie ponad 100 oczek. | P | F |
Rzucamy ośmiokrotnie standardową sześcienną kostką do gry. Liczba  jest iloczynem wszystkich otrzymanych liczb oczek. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
jest iloczynem wszystkich otrzymanych liczb oczek. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczba  może być równa 35. może być równa 35. | P | F |
Liczba  może być równa 1024. może być równa 1024. | P | F |

