Na osi liczbowej zaznaczono dwa punkty opisane wyrażeniami algebraicznymi.
![]()
Wyrażenie opisujące odległość tych punktów na osi liczbowej jest równe
A) 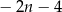 B)
B) 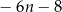 C)
C) 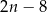 D)
D) 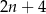
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Na osi liczbowej zaznaczono dwa punkty opisane wyrażeniami algebraicznymi.
![]()
Wyrażenie opisujące odległość tych punktów na osi liczbowej jest równe
A) 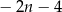 B)
B) 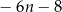 C)
C) 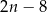 D)
D) 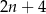
Wykres funkcji liniowej 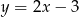 przecina oś
przecina oś 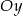 w punkcie o współrzędnych
w punkcie o współrzędnych
A) 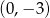 B)
B) 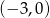 C)
C) 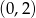 D)
D) 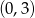
Wykres funkcji liniowej 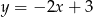 przecina oś
przecina oś 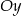 w punkcie o współrzędnych
w punkcie o współrzędnych
A) 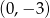 B)
B) 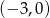 C)
C) 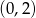 D)
D) 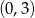
Wiedząc, że boki trójkąta prostokątnego mają długości: 20, 15, 25, wyznacz długość wysokości opuszczonej na przeciwprostokątną.
Boki trójkąta prostokątnego mają długości 10,24,26. Oblicz długość wysokości opuszczonej na przeciwprostokątną.
Mediana kolejnych pięciu liczb naturalnych jest równa 7. Najmniejsza z tych liczb to
A) 5 B) 9 C) 8 D) 11
Mediana kolejnych pięciu liczb naturalnych jest równa 8. Najmniejsza z tych liczb to
A) 9 B) 10 C) 6 D) 12
Mediana kolejnych pięciu liczb naturalnych jest równa 12. Najmniejsza z tych liczb to
A) 16 B) 14 C) 13 D) 10
Mediana kolejnych sześciu liczb naturalnych jest równa 47,5. Najmniejsza z tych liczb to
A) 46 B) 41 C) 45 D) 44
Zapisz wzór i narysuj wykres funkcji, która każdej liczbie przyporządkowuje liczbę o 2 większą od połowy tej liczby.
Różnica miar dwóch kątów rozwartych trapezu jest równa 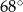 . Dodatnia różnica miar kątów ostrych tego trapezu jest więc równa
. Dodatnia różnica miar kątów ostrych tego trapezu jest więc równa
A) 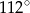 B)
B) 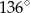 C)
C) 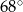 D)
D) 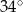
Odczytaj z wykresu, dla jakich argumentów funkcja rośnie, a dla jakich maleje.
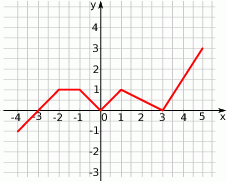
Odczytaj z wykresu, dla jakich argumentów funkcja rośnie, a dla jakich maleje.
Na rysunku przedstawiono oś liczbową, na której kropkami zaznaczono cztery liczby.
![]()
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Iloczyn dwóch spośród zaznaczonych liczb jest równy iloczynowi dwóch pozostałych. | P | F |
| Suma dwóch spośród zaznaczonych liczb jest równa sumie dwóch pozostałych. | P | F |
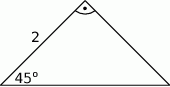
Oblicz pole trójkąta przedstawionego na rysunku.
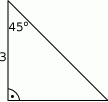
Oblicz pole trójkąta przedstawionego na rysunku.
Hania pokonuje drogę 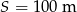 z domu do szkoły w czasie 30 min. Z jaką średnią prędkością idzie Hania?
z domu do szkoły w czasie 30 min. Z jaką średnią prędkością idzie Hania?
A) 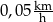 B)
B) 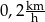 C)
C) 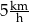 D)
D) 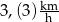
Samochód przejechał ze stałą prędkością trasę o długości 18 kilometrów w czasie 12 minut. Samochód przejechał tę trasę z prędkością
A) 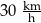 B)
B) 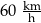 C)
C) 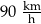 D)
D) 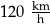
Paweł przejechał na rowerze trasę długości 700 m w czasie 2 min. Prędkość średnia, jaką uzyskał Paweł na tej trasie, jest równa
A) 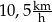 B)
B) 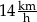 C)
C) 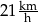 D)
D) 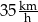
Odcinkowy pomiar prędkości polega na wyznaczeniu średniej prędkości samochodu na określonym odcinku drogi. Na początku i na końcu takiego odcinka ustawiono znaki drogowe informujące o rozpoczęciu i zakończeniu pomiaru (zobacz rysunek).

Samochód osobowy przejechał w 2 minuty taki odcinek drogi o długości 3 km. Wyznaczona prędkość tego samochodu na objętym pomiarem odcinku drogi była równa
A) 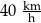 B)
B) 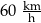 C)
C) 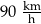 D)
D) 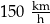
Kasia przejechała na rowerze trasę długości 900 m w czasie 3 min. Prędkość średnia, jaką uzyskała Kasia na tej trasie, jest równa
A) 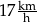 B)
B) 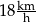 C)
C) 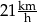 D)
D) 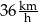
Sonda Voyager 2, która została wysłana w przestrzeń kosmiczną w 1977 roku, w 2007 roku znalazła się na granicy heliosfery w odległości 17,5 bilionów kilometrów od słońca. Od tej pory sonda oddala się od słońca ze stałą prędkością równą 15,35 km/s. Prędkość sondy Voyager 2 po opuszczeniu heliosfery jest równa
A) 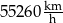 B)
B) 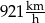 C)
C) 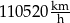 D)
D) 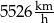
Jeżeli kilogram ziemniaków kosztuje  złotych, a 5 kilogramów ziemniaków kosztuje
złotych, a 5 kilogramów ziemniaków kosztuje 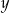 złotych, to
złotych, to
A) 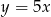 B)
B) 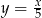 C)
C) 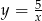 D)
D) 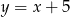
Jeżeli kilogram ziemniaków kosztuje  złotych, a za 5 zł kupiono
złotych, a za 5 zł kupiono 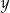 kg ziemniaków, to
kg ziemniaków, to
A) 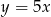 B)
B) 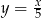 C)
C) 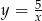 D)
D) 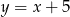
Koncern paliwowy podnosił dwukrotnie w jednym tygodniu cenę benzyny, pierwszy raz o 10%, a drugi raz o 5%. Po obu tych podwyżkach jeden litr benzyny, wyprodukowanej przez ten koncern, kosztuje 4,62 zł. Oblicz cenę jednego litra benzyny przed omawianymi podwyżkami.
W poniedziałek cenę pewnego towaru zwiększono o 10%, zaś w środę zmniejszono o 15%. Oblicz początkową cenę tego towaru, jeśli ostatecznie po tych zmianach wynosiła 187 zł.
W poniedziałek cenę pewnego towaru zmniejszono o 10%, zaś w środę zwiększono o 20%. Oblicz początkową cenę tego towaru, jeśli ostatecznie po tych zmianach wynosiła 324 zł.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| W pięciu rzutach standardową sześcienną kostką do gry, jeżeli wynik każdego rzutu będzie inny, można otrzymać łącznie dokładnie 20 oczek. | P | F |
| W 16 rzutach standardową sześcienną kostką do gry można otrzymać łącznie ponad 100 oczek. | P | F |
Rzucamy ośmiokrotnie standardową sześcienną kostką do gry. Liczba  jest iloczynem wszystkich otrzymanych liczb oczek. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
jest iloczynem wszystkich otrzymanych liczb oczek. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Liczba  może być równa 35. może być równa 35. | P | F |
Liczba  może być równa 1024. może być równa 1024. | P | F |
W prostopadłościennym akwarium, o wymiarach podanych na rysunku, woda sięga  jego wysokości.
jego wysokości.
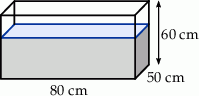
Ile litrów wody jest w akwarium?
A) 16000 litrów B) 1600 litrów C) 160 litrów D) 16 litrów
W prostopadłościennym akwarium, o wymiarach podanych na rysunku, woda sięga 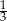 jego wysokości.
jego wysokości.
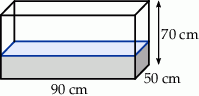
Ile litrów wody jest w akwarium?
A) 105000 litrów B) 105 litrów C) 1050 litrów D) 10500 litrów
W pewnym zakładzie każdy z pracowników codziennie maluje taką samą liczbę jednakowych ozdób. Pracownicy potrzebowali 12 dni roboczych, aby wykonać zamówienie. Gdyby było ich o dwóch więcej, to czas wykonania tego zamówienia byłby o 3 dni krótszy. Liczbę pracowników  tego zakładu można obliczyć, rozwiązując równanie
tego zakładu można obliczyć, rozwiązując równanie
A) 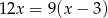 B)
B) 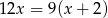 C)
C) 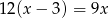 D)
D) 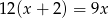
Maszyna produkcyjna wytwarza codziennie tę samą liczbę elementów. Wykonanie pewnego zamówienia wymaga jednoczesnej pracy pewnej liczby takich maszyn przez 15 dni. Gdyby jednak zwiększyć liczbę pracujących maszyn o 4, to czas wykonania zamówienia skróciłby się o 2 dni. Liczbę maszyn potrzebnych do realizacji zamówienia można obliczyć, rozwiązując równanie
A) 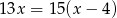 B)
B) 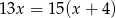 C)
C) 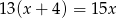 D)
D) 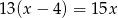
W pudełku jest 2400 kuponów, wśród których 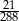 stanowią kupony przegrywające, a pozostałe kupony są wygrywające. Z tego pudełka w sposób losowy wyciągamy jeden kupon. Prawdopodobieństwo zdarzenia polegającego na tym, że wyciągniemy kupon wygrywający, jest równe
stanowią kupony przegrywające, a pozostałe kupony są wygrywające. Z tego pudełka w sposób losowy wyciągamy jeden kupon. Prawdopodobieństwo zdarzenia polegającego na tym, że wyciągniemy kupon wygrywający, jest równe
A) 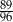 B)
B) 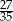 C)
C) 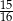 D)
D) 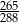
Na rysunku przedstawiono okrąg o środku 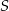 i kąt wpisany o mierze
i kąt wpisany o mierze 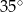 .
.
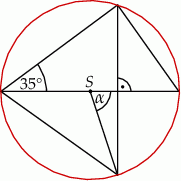
Zaznaczony na rysunku kąt  ma miarę
ma miarę
A) 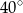 B)
B) 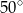 C)
C) 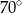 D)
D) 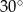
W prostopadłościanie pola trzech ścian o wspólnym wierzchołku są równe 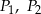 i
i 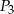 . Oblicz objętość tego prostopadłościanu.
. Oblicz objętość tego prostopadłościanu.
Oblicz pole i obwód koła o średnicy 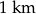 .
.
Oblicz pole i obwód koła o średnicy 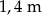 .
.
Oblicz pole i obwód koła o średnicy 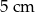 .
.
Oblicz pole i obwód koła o średnicy 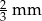 .
.
Dane są trzy liczby:
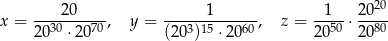
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Dwie spośród liczb 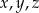 są większe od liczby są większe od liczby 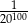 . . | P | F |
Różnica dwóch spośród liczb 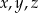 jest równa 0. jest równa 0. | P | F |
