Jakie pole ma trójkąt równoboczny o boku 4?
/Szkoła podstawowa
Trzy rodziny kupiły działki pod zabudowę. Pierwsza rodzina kupiła  całego terenu, druga
całego terenu, druga 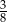 reszty, a pozostałą część, równą
reszty, a pozostałą część, równą 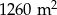 , kupiła trzecia rodzina. Jaka była powierzchnia całego zakupionego terenu i jakiej wielkości była każda z działek?
, kupiła trzecia rodzina. Jaka była powierzchnia całego zakupionego terenu i jakiej wielkości była każda z działek?
Na wycieczkę do kina miała pójść grupa 28 uczniów klasy IIb. Ostatecznie jednak liczba osób biorących udział w wycieczce zmniejszyła się o jedną osobę. Stało się tak, gdyż z wycieczki zrezygnowało 25% dziewcząt, oraz do grupy dołączyło kilku chłopców z klasy IIa i liczba chłopców biorących udział w wycieczce zwiększyła się o 25%. Ilu chłopców i ile dziewcząt wzięło udział w wycieczce?
Krawędź sześcianu ma długość 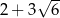 .
.
Suma długości wszystkich krawędzi sześcianu jest równa A/B.
A) 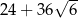 B)
B) 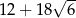
Pole powierzchni jednej ściany sześcianu jest równe C/D.
C) 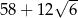 D)
D) 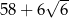
Na parkingu w kształcie rombu o boku długości 20 m i kącie ostrym 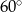 ma powstać betonowa nawierzchnia, do wykonania której potrzeba 20 kg betonu na
ma powstać betonowa nawierzchnia, do wykonania której potrzeba 20 kg betonu na 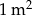 . Czy 12 ton betonu wystarczy do wykonania tej nawierzchni?
. Czy 12 ton betonu wystarczy do wykonania tej nawierzchni?
Udowodnij, że w trójkącie równoramiennym wysokości poprowadzone do równych boków są równej długości.
Wyznacz kąty trapezu równoramiennego, jeśli miara jednego z nich jest większa od miary drugiego o 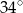 .
.
Wyznacz kąty trapezu równoramiennego, jeśli miara jednego z nich jest większa od miary drugiego o 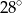 .
.
Wyznacz kąty trapezu równoramiennego, jeśli miara jednego z nich jest 5 razy większa od miary drugiego.
Wyznacz kąty trapezu równoramiennego, jeśli miara jednego z nich jest 4 razy większa od miary drugiego.
Promocja w zakładzie optycznym jest związana z wiekiem klienta i polega na tym, że klient otrzymuje tyle procent zniżki, ile ma lat.
Cena okularów bez promocji wynosi 240 zł. Ile zapłaci za te okulary klient, który ma 35 lat?
A) 84 zł B) 132 zł C) 156 zł D) 205 zł
Promocja w zakładzie optycznym jest związana z wiekiem klienta i polega na tym, że klient otrzymuje tyle procent zniżki, ile ma lat.
Okulary bez promocji kosztują 450 zł, a klient zgodnie z obowiązującą promocją może je kupić za 288 zł. Ile lat ma ten klient?
A) 64 B) 56 C) 44 D) 36
Oblicz miarę kąta ostrego, pod którym przecinają się przekątne równoległoboku przedstawionego na rysunku.
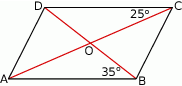
Oblicz miarę kąta rozwartego, pod którym przecinają się przekątne równoległoboku przedstawionego na rysunku.
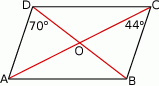
Oblicz miarę kąta ostrego, pod którym przecinają się przekątne równoległoboku przedstawionego na rysunku.
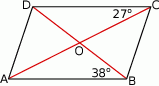
Obwód trójkąta 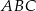 , przedstawionego na rysunku, jest równy
, przedstawionego na rysunku, jest równy
A) 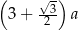 B)
B) 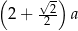 C)
C) 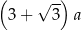 D)
D) 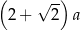
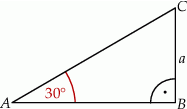
Obwód trójkąta 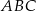 , przedstawionego na rysunku, jest równy
, przedstawionego na rysunku, jest równy
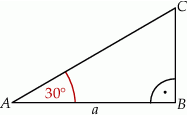
A) 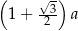 B)
B) 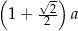 C)
C) 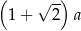 D)
D) 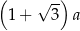
Jeżeli 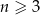 , to liczbę przekątnych wielokąta wypukłego o
, to liczbę przekątnych wielokąta wypukłego o  bokach można obliczyć ze wzoru
bokach można obliczyć ze wzoru
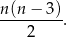
Wielokąt, który ma cztery razy więcej przekątnych niż boków ma A/B boków.
A) 10 B) 11
Liczba przekątnych wielokąta o 222 bokach jest liczbą C/D.
C) nieparzystą D) parzystą
Jeżeli 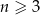 , to liczbę przekątnych wielokąta wypukłego o
, to liczbę przekątnych wielokąta wypukłego o  bokach można obliczyć ze wzoru
bokach można obliczyć ze wzoru
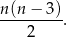
Która z liczb nie jest liczbą przekątnych pewnego wielokąta wypukłego?
A) 5 B) 9 C) 10 D) 14 E) 20
Na diagramie przedstawiono wyniki sprawdzianu z matematyki przeprowadzonego w klasie VIIIc. Za rozwiązanie wszystkich zadań można było uzyskać maksymalnie 30 punktów, ale nikt nie zdobył więcej niż 25 punktów oraz nikt nie otrzymał mniej niż 10 punktów.
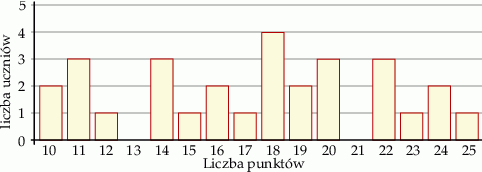
Wynik powyżej 50% punktów możliwych do zdobycia uzyskało A/B uczniów.
A) 19 B) 20
Dokładnie 12 uczniów uzyskało wynik C/D punktów możliwych do zdobycia.
C) powyżej 60% D) poniżej 40%
Poniżej opisano kilka zależności.
1) Im większy bok kwadratu, tym większe jego pole.
2) Im większy bok kwadratu, tym większy jego obwód.
3) Im większa cena 1 kg ziemniaków, tym więcej zapłacimy za 2 kg.
4) Im większa cena 1 kg ziemniaków, tym mniej kupimy za 4 zł.
5) Im więcej wydaliśmy z 10 zł, tym mniej nam zostało.
Które z przedstawionych zależności są proporcjonalnością prostą?
A) 1, 2 i 3 B) tylko 2 i 3 C) tylko 1 i 2 D) tylko 3 i 4
Poniżej opisano kilka zależności.
1) Im większy bok kwadratu, tym większe jego pole.
2) Im większy bok kwadratu, tym większy jego obwód.
3) Im większa cena 1 kg ziemniaków, tym więcej zapłacimy za 2 kg.
4) Im większa cena 1 kg ziemniaków, tym mniej kupimy za 4 zł.
5) Im więcej wydaliśmy z 10 zł, tym mniej nam zostało.
Która z przedstawionych powyżej zależności jest opisana danym wykresem
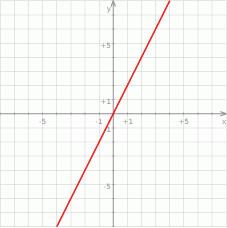
A) 5 B) 4 C) 3 D) 2
Poniżej opisano kilka zależności.
1) Im większy bok kwadratu, tym większe jego pole.
2) Im większy bok kwadratu, tym większy jego obwód.
3) Im większa cena 1 kg ziemniaków, tym więcej zapłacimy za 2 kg.
4) Im większa cena 1 kg ziemniaków, tym mniej kupimy za 4 zł.
5) Im więcej wydaliśmy z 10 zł, tym mniej nam zostało.
Która z przedstawionych powyżej zależności jest opisana danym wykresem
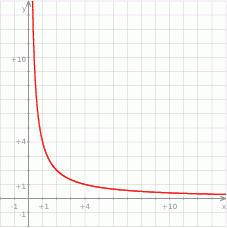
A) 4 B) 3 C) 2 D) 1
Poniżej opisano kilka zależności.
1) Im większy bok kwadratu, tym większe jego pole.
2) Im większy bok kwadratu, tym większy jego obwód.
3) Im większa cena 1 kg ziemniaków, tym więcej zapłacimy za 2 kg.
4) Im większa cena 1 kg ziemniaków, tym mniej kupimy za 4 zł.
5) Im więcej wydaliśmy z 10 zł, tym mniej nam zostało.
Które z przedstawionych zależności są proporcjonalnością odwrotną?
A) 4, 5,6 B) tylko 4 C) tylko 5 D) 3, 4, 5
W układzie współrzędnych wyznaczono odcinek o końcach w punktach 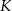 ,
, 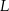 i środku w punkcie
i środku w punkcie 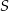 . Punkt
. Punkt 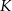 ma współrzędne
ma współrzędne 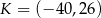 , a punkt
, a punkt 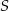 współrzędne
współrzędne 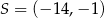 . Na którym rysunku zacieniowana część płaszczyzny zawiera punkt
. Na którym rysunku zacieniowana część płaszczyzny zawiera punkt 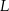 ?
?
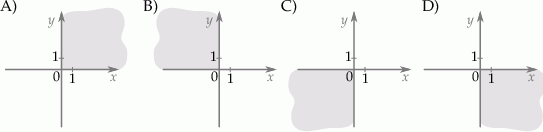
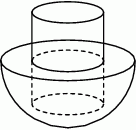
Pojemnik z kremem ma kształt walca o promieniu podstawy 4 cm i wysokości 4,5 cm. Po jego otwarciu okazało się, że krem wypełnia tylko wyżłobioną w pojemniku półkulę o promieniu 3 cm. Ile razy objętość tej półkuli jest mniejsza od objętości walca? Zapisz obliczenia.
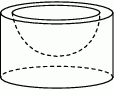
Pojemnik z kremem ma kształt walca o promieniu podstawy 5 cm i wysokości 5,12 cm. Po jego otwarciu okazało się, że krem wypełnia tylko wyżłobioną w pojemniku półkulę o promieniu 4 cm. Ile razy objętość tej półkuli jest mniejsza od objętości walca? Zapisz obliczenia.
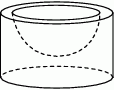
Element mechaniczny pewnego urządzenia ma kształt pełnego metalowego walca o wysokości 10 cm i promieniu podstawy 2 cm, który do połowy swojej wysokości jest umieszczony w gumowej półkuli o promieniu 6 cm. Oblicz stosunek objętości gumy do objętości metalu potrzebnych do wykonania tego elementu.
W czworokącie 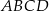 boki
boki 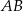 ,
, 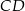 i
i 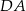 mają równe długości, a kąt
mają równe długości, a kąt 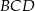 ma miarę
ma miarę 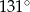 . Przekątna
. Przekątna 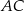 dzieli ten czworokąt na trójkąt równoboczny i na trójkąt równoramienny (zobacz rysunek).
dzieli ten czworokąt na trójkąt równoboczny i na trójkąt równoramienny (zobacz rysunek).
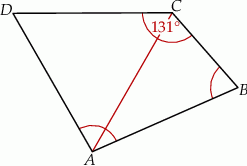
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Kąt 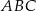 ma miarę ma miarę 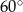 . . | P | F |
Kąt 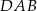 ma miarę ma miarę 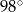 . . | P | F |
W czworokącie 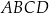 boki
boki 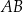 ,
, 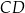 i
i 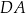 mają równe długości, a kąt
mają równe długości, a kąt 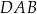 ma miarę
ma miarę 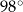 . Przekątna
. Przekątna 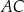 dzieli ten czworokąt na trójkąt równoboczny i na trójkąt równoramienny (zobacz rysunek).
dzieli ten czworokąt na trójkąt równoboczny i na trójkąt równoramienny (zobacz rysunek).
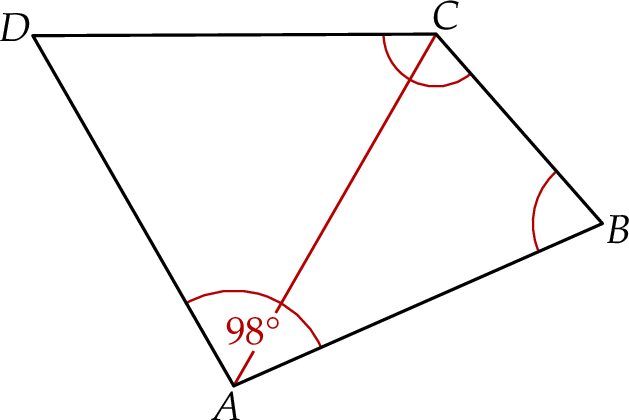
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Kąt 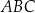 ma miarę ma miarę 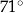 . . | P | F |
Kąt 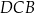 ma miarę ma miarę 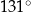 . . | P | F |
Na siatce kwadratowej narysowano trójkąt. Bok kwadratu siatki jest równy 1.
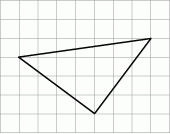
Obwód narysowanego trójkąta jest równy
A) 76 B) 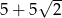 C)
C) 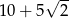 D) 75
D) 75
W sadzie rosną drzewa owocowe: grusze i jabłonie. Liczba grusz jest o 40% większa od liczby jabłoni. Jabłoni jest o 50 mniej niż grusz. Ile jabłoni rośnie w tym sadzie?
A) 20 B) 30 C) 70 D) 125
W sadzie rosną drzewa owocowe: grusze i jabłonie. Liczba jabłoni jest o 40% większa od liczby grusz. Grusz jest o 30 mniej niż jabłoni. Ile jabłoni rośnie w tym sadzie?
A) 90 B) 105 C) 75 D) 125
Cena brutto = cena netto + podatek VAT
Jeżeli stawka podatku VAT jest równa 22% i cenna brutto towaru jest równa 4392 zł to cena netto tego towaru jest równa
A) 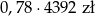 B)
B) 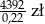 C)
C) 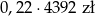 D)
D) 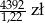
Liczby naturalne od 1 do 8 umieszczono w wierzchołkach sześcianu w ten sposób, że w żadnych dwóch wierzchołkach nie umieszczono tej samej liczby. Następnie na każdej krawędzi sześcianu umieszczono sumę liczb, które znajdują się na końcach tej krawędzi, a na środku każdej ściany umieszczono sumę liczb, które znajdują w wierzchołkach tej ściany. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Suma wszystkich liczb umieszczonych na krawędziach sześcianu jest równa 72. | P | F |
| Suma wszystkich liczb umieszczonych w środkach ścian sześcianu jest równa 144. | P | F |

