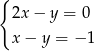Basia stwierdziła, że w ciągu dnia zjadła produkty, które łącznie zawierały 151,2 g tłuszczu. Obliczyła, że o 44% przekroczyła normę dzienną spożycia tłuszczu dla piętnastolatków. Ile gramów tłuszczu wynosi norma dzienna? O ile gramów Basia przekroczyła tę normę?
/Szkoła podstawowa
Oblicz miarę kąta 
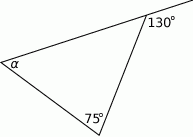
Oblicz miarę kąta 
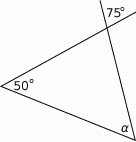
Oblicz miarę kąta 
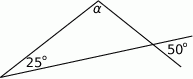
Oblicz miarę kąta 
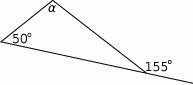
Oblicz miarę kąta 
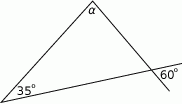
Oblicz miarę kąta 
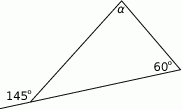
Na statku wycieczkowym są 33 miejsca dla pasażerów. Uczniowie klas IIIa i IIIb planują wycieczkę tym statkiem. W każdej z tych klas jest mniej niż 33 uczniów. Aby wszystkie miejsca dla pasażerów były na statku zajęte, należy do wszystkich uczniów klasy IIIa dołączyć 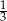 uczniów klasy IIIb albo do wszystkich uczniów klasy IIIb dołączyć
uczniów klasy IIIb albo do wszystkich uczniów klasy IIIb dołączyć 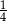 uczniów klasy IIIa. Ilu uczniów jest w każdej z tych klas?
uczniów klasy IIIa. Ilu uczniów jest w każdej z tych klas?
Pokój ma wymiary 6 m na 6,75 m. Na  powierzchni podłogi położono parkiet, na reszcie 150 kwadratowych płytek terakoty. Jakie wymiary ma płytka terakoty i ile zapłacono za parkiet, jeśli
powierzchni podłogi położono parkiet, na reszcie 150 kwadratowych płytek terakoty. Jakie wymiary ma płytka terakoty i ile zapłacono za parkiet, jeśli 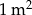 parkietu kosztuje 90 zł?
parkietu kosztuje 90 zł?
Przekątne prostokąta 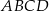 przedstawionego na rysunku przecinają się pod kątem
przedstawionego na rysunku przecinają się pod kątem 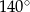 .
.
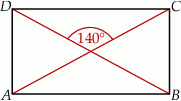
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Kąt 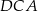 ma miarę ma miarę 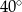 . . | P | F |
Kąt 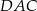 ma miarę ma miarę 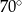 . . | P | F |
Przekątne prostokąta 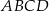 przedstawionego na rysunku przecinają się pod kątem
przedstawionego na rysunku przecinają się pod kątem 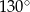 .
.
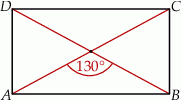
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Kąt 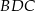 ma miarę ma miarę 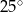 . . | P | F |
Kąt 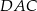 ma miarę ma miarę 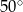 . . | P | F |
Liczbę 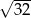 można przedstawić w postaci
można przedstawić w postaci
A) 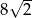 B)
B) 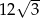 C)
C) 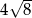 D)
D) 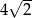
Pan Kamil wyjechał o godzinie 9:00 w podróż samochodową z Torunia do Warszawy. Wykres przedstawia jego odległość od Torunia w zależności od czasu jazdy.
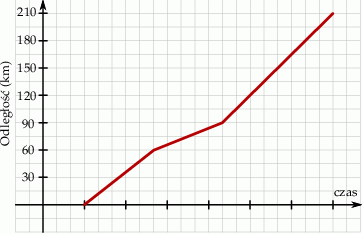
Średnia prędkość z jaką pokonał ten dystans jest równa 70 km/h. Oblicz z jaką największą prędkością poruszał się Pan Kamil w trakcie swojej podróży do Warszawy.
Liczbę naturalną  najpierw zwiększono o 40%, a następnie zmniejszono o 20%. W wyniku tych operacji liczbę
najpierw zwiększono o 40%, a następnie zmniejszono o 20%. W wyniku tych operacji liczbę 
A) zmniejszono o 12% B) zwiększono o 12%
C) zwiększono o 20% D) zmniejszono o 30%
Liczbę  najpierw zwiększono o 30%, a następnie zmniejszono o 30%. W wyniku tych operacji
najpierw zwiększono o 30%, a następnie zmniejszono o 30%. W wyniku tych operacji
A) liczbę  zmniejszono o 12% B) liczbę
zmniejszono o 12% B) liczbę  zwiększono o 12%
zwiększono o 12%
C) liczba  nie zmieniła się D) liczbę
nie zmieniła się D) liczbę  zmniejszono o 9%
zmniejszono o 9%
Liczbę  najpierw zmniejszono o 40%, a następnie zwiększono o 20%. W wyniku tych operacji liczbę
najpierw zmniejszono o 40%, a następnie zwiększono o 20%. W wyniku tych operacji liczbę 
A) zmniejszono o 28% B) zwiększono o 12%
C) zmniejszono o 8% D) zmniejszono o 20%
Oblicz obwód okręgu wpisanego w kwadrat, którego bok ma długość 10cm.
Uzasadnij, że jeśli liczba jest podzielna przez 15 i przez 14, to jest podzielna przez 10.
Podstawa ostrosłupa prawidłowego czworokątnego ma pole 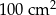 , a jego pole powierzchni bocznej jest równe
, a jego pole powierzchni bocznej jest równe 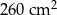 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Dwunastu malarzy pracując z jednakową wydajnością pomalowało burtę statku w ciągu 8 godzin. Ilu malarzy powinno malować tę burtę, aby tę samą pracę wykonać w ciągu 6 godzin?
A) 14 B) 16 C) 18 D) 20
Osiem pomp napełnia cały zbiornik w ciągu 6 godzin. Każda pompa pracuje z taką samą stałą wydajnością. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Sześć pomp napełni cały zbiornik w ciągu 9 godzin. | P | F |
| Połowę zbiornika w ciągu 4 godzin napełni 6 pomp. | P | F |
Sześć maszyn produkuje pewną partię jednakowych butelek z tworzywa sztucznego przez 4 godziny. Każda z maszyn pracuje z taką samą stałą wydajnością.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Przez 8 godzin taką samą partię butelek wykonają 3 takie maszyny. | P | F |
| Połowę partii takich butelek 6 maszyn wykona przez 2 godziny. | P | F |
W pewnej fabryce są dwie linie produkcyjne produkujące identyczne układy elektroniczne. Obydwie linie produkcyjne wytwarzają łącznie 720 układów w ciągu 8 godzin, a sama druga linia produkcyjna wytwarza 558 układów w ciągu 12 godzin.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Pierwsza linia produkcyjna pracuje z mniejszą wydajnością niż druga. | P | F |
| Pierwsza linia produkcyjna w ciągu 8 godzin wykonuje 352 układy. | P | F |
Wartość wyrażenia 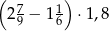 wynosi
wynosi
A) 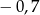 B) 2,6 C) 5 D)
B) 2,6 C) 5 D) 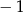
Wartość wyrażenia 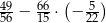 jest równa
jest równa
A) 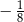 B)
B) 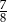 C)
C) 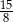 D) 2
D) 2
Wartość wyrażenia 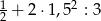 jest równa
jest równa
A) 2 B) 1,875 C)  D)
D) 
Wartość wyrażenia 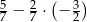 jest równa
jest równa
A) 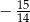 B)
B) 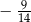 C)
C)  D)
D) 
Wartość wyrażenia 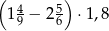 wynosi
wynosi
A) 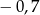 B)
B) 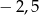 C) 5 D)
C) 5 D) 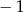
Wartość wyrażenia 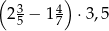 wynosi
wynosi
A) 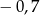 B) 2,6 C) 5 D) 3,6
B) 2,6 C) 5 D) 3,6
Dane są cztery wyrażenia:

Jedno z tych wyrażeń przyjmuje wartość 0 dla 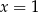 oraz dla
oraz dla 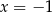 . Które to wyrażenie?
. Które to wyrażenie?
A) 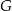 B)
B) 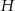 C)
C) 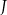 D)
D) 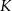
Dane są cztery wyrażenia:

Jedno z tych wyrażeń przyjmuje wartość 0 dla 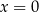 oraz dla
oraz dla 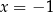 . Które to wyrażenie?
. Które to wyrażenie?
A) 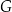 B)
B) 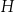 C)
C) 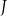 D)
D) 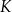
Dane są cztery wyrażenia:

Jedno z tych wyrażeń przyjmuje tą samą wartość dla 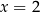 oraz dla
oraz dla 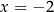 . Które to wyrażenie?
. Które to wyrażenie?
A) 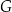 B)
B) 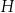 C)
C) 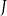 D)
D) 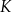
W ośrodku szkoleniowym są jednakowe stoliki, których blaty mają kształt trapezów równoramiennych, jak przedstawiono na rysunku 1.

Stoliki można ze sobą łączyć na różne sposoby. Na rysunkach przedstawiono trzy przykładowe zestawienia stolików w stoły konferencyjne oraz sposoby ustawienia przy nich krzeseł.
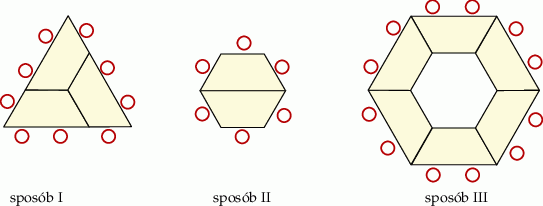
W ośrodku jest 36 stolików. Postanowiono je ustawić w jeden z trzech sposobów pokazanych na powyższych rysunkach. Które z poniższych zdań jest fałszywe?
A) Po ustawieniu wszystkich stolików w sposób I uzyska się tyle samo miejsc siedzących, ile powstaje po ustawieniu wszystkich stolików w sposób II.
B) Najmniejszą liczbę miejsc siedzących uzyska się po ustawieniu wszystkich stolików w sposób III.
C) Po ustawieniu wszystkich stolików w sposób I uzyska się 108 miejsc siedzących.
D) Po ustawieniu wszystkich stolików w sposób II uzyska się 96 miejsc siedzących.
W ośrodku szkoleniowym są jednakowe stoliki, których blaty mają kształt trapezów równoramiennych, jak przedstawiono na rysunku 1.

Stoliki można ze sobą łączyć na różne sposoby. Na rysunkach przedstawiono trzy przykładowe zestawienia stolików w stoły konferencyjne oraz sposoby ustawienia przy nich krzeseł.
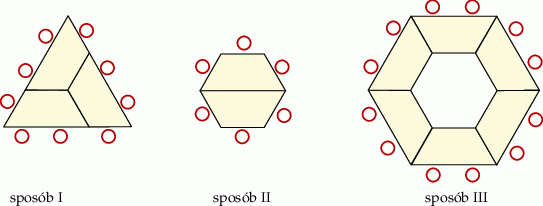
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Kąty trapezu przedstawionego na rysunku 1 mają miary: 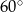 , , 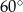 , , 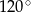 , , 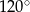 . . | P | F |
| Krótsza podstawa tego trapezu jest 2 razy krótsza od jego dłuższej podstawy. | P | F |
W pewnym zakładzie pracy każdy z pracowników codziennie montuje taką samą liczbę jednakowych podzespołów. Pracownicy potrzebowali 12 dni roboczych, aby wykonać zamówienie. Gdyby wydajność każdego z pracowników była wyższa o 20%, to wykonaliby zamówienie w
A) 8 dni B) 9 dni C) 10 dni D) 11 dni
Liczbą podzielną przez 36 jest
A) 345222 B) 986472 C) 322144 D) 631422
W prostokącie 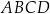 bok
bok 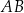 jest cztery razy dłuższy od boku
jest cztery razy dłuższy od boku 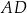 . Punkty
. Punkty 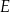 i
i 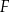 dzielą odcinek
dzielą odcinek 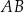 na trzy równe części (zobacz rysunek).
na trzy równe części (zobacz rysunek).
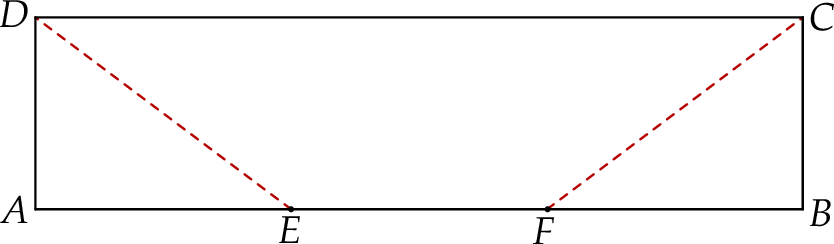
Oblicz pole trapezu 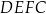 jeżeli wiadomo, że jego obwód jest równy 52 cm.
jeżeli wiadomo, że jego obwód jest równy 52 cm.
Z urny, w której jest wyłącznie 18 kul białych i 12 kul czarnych, losujemy 1 kulę.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Prawdopodobieństwo wylosowania kuli białej jest równe 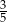 . . | P | F |
Prawdopodobieństwo wylosowania kuli czarnej jest mniejsze od 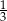 | P | F |
Z urny, w której jest wyłącznie 16 kul białych i 24 kule czarne, losujemy 1 kulę.
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Prawdopodobieństwo wylosowania kuli białej jest równe  . . | P | F |
Prawdopodobieństwo wylosowania kuli czarnej jest większe od  | P | F |
Para liczb 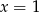 i
i 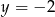 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań
A) 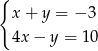 B)
B) 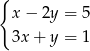 C)
C) 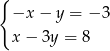 D)
D) 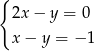
Para liczb 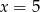 i
i 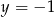 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań
A) 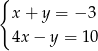 B)
B) 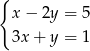 C)
C) 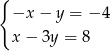 D)
D) 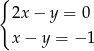
Para liczb 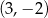 spełnia układ równań
spełnia układ równań
A) 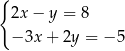 B)
B) 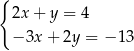
C) 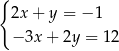 D)
D) 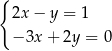
Para liczb 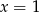 i
i 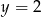 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań
A) 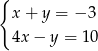 B)
B) 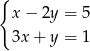 C)
C) 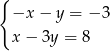 D)
D) 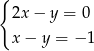
Para liczb 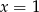 i
i 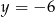 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań
A) 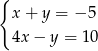 B)
B) 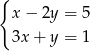 C)
C) 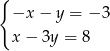 D)
D)