W trakcie przygotowań do zawodów pływackich Szymon i Bartosz pływali równolegle do brzegu jeziora na dystansie 2 km. Wykresy przedstawiają zależność między odległością chłopców od miejsca startu, a czasem pływania.
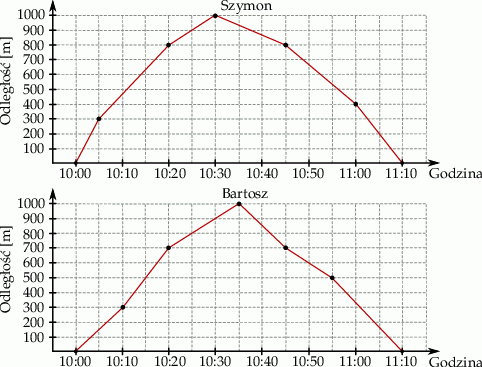
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Bartosz pokonał dystans 2 km ze średnią prędkością większą niż Szymon. | P | F |
| Bartosz przepłynął obie połowy dystansu 2 km z tą samą prędkością średnią. | P | F |

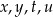 zapisane za pomocą wyrażeń arytmetycznych:
zapisane za pomocą wyrażeń arytmetycznych: 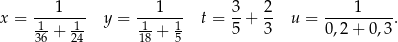

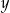
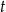

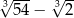 jest równa
jest równa 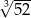
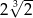
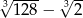 jest równa
jest równa 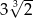
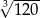
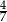 , a jeżeli do licznika i do mianownika dodamy 1, to otrzymamy
, a jeżeli do licznika i do mianownika dodamy 1, to otrzymamy 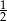 . Wyznacz ten ułamek.
. Wyznacz ten ułamek. 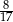 . Wyznacz ten ułamek.
. Wyznacz ten ułamek. 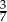 , a jeżeli do licznika i do mianownika dodamy 1, to otrzymamy
, a jeżeli do licznika i do mianownika dodamy 1, to otrzymamy 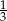 . Wyznacz ten ułamek.
. Wyznacz ten ułamek.  , a jeżeli do licznika i do mianownika dodamy 6, to otrzymamy
, a jeżeli do licznika i do mianownika dodamy 6, to otrzymamy 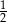 . Wyznacz ten ułamek.
. Wyznacz ten ułamek. 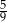 . Wyznacz ten ułamek.
. Wyznacz ten ułamek. 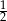 . Wyznacz ten ułamek.
. Wyznacz ten ułamek. 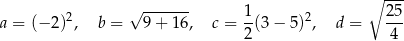
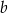 jest większa niż liczba
jest większa niż liczba  .
.  jest dwa razy mniejsza niż liczba
jest dwa razy mniejsza niż liczba  .
. 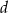 jest 2 razy mniejsza niż liczba
jest 2 razy mniejsza niż liczba 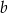 .
.  jest większa niż liczba
jest większa niż liczba 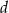 .
. 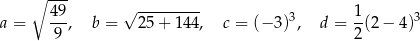
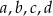 są dokładnie dwie liczby ujemne.
są dokładnie dwie liczby ujemne.  jest większa niż liczba
jest większa niż liczba  .
. 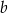 jest o 21 większa od liczby
jest o 21 większa od liczby 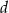 .
.  jest o 23 większa od liczby
jest o 23 większa od liczby  .
.  jest liczba, która nie jest liczbą całkowitą.
jest liczba, która nie jest liczbą całkowitą. 
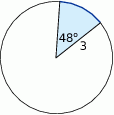
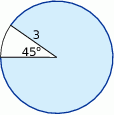
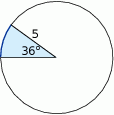
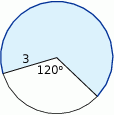
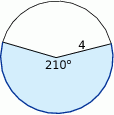
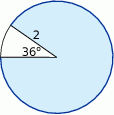
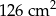 . Jaką długość ma najkrótsza z wysokości tego trójkąta?
. Jaką długość ma najkrótsza z wysokości tego trójkąta? 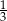
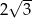
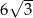
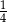
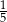
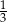
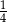
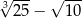 jest liczbą dodatnią.
jest liczbą dodatnią.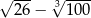 jest liczbą ujemną.
jest liczbą ujemną. 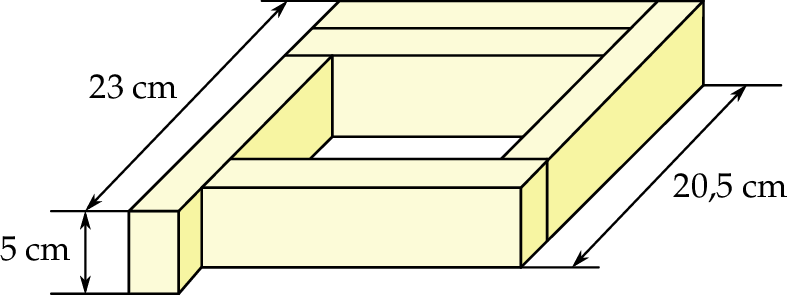
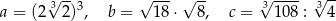
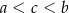
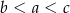
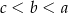
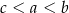
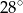 .
. 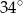 .
. 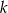 przechodzi przez punkty
przechodzi przez punkty 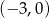 i
i 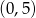 . Ustal w jakich punktach przecina osie układu współrzędnych prosta, która jest symetryczna do prostej
. Ustal w jakich punktach przecina osie układu współrzędnych prosta, która jest symetryczna do prostej 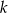 względem:
względem: 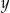 ;
;  ;
; 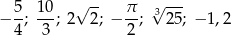
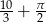
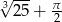
 jest podzielna przez 3, ale nie jest podzielna przez 6. Trzy początkowe cyfry tej liczby to: 4, 1, 3, a dwie pozostałe cyfry są większe od 4. Ile może być równe
jest podzielna przez 3, ale nie jest podzielna przez 6. Trzy początkowe cyfry tej liczby to: 4, 1, 3, a dwie pozostałe cyfry są większe od 4. Ile może być równe  ? Podaj wszystkie możliwości.
? Podaj wszystkie możliwości. 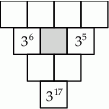
 .
.  .
.