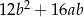Samochód osobowy przebył drogę 120 km w czasie 75 minut. Prędkość średnia busa na tej samej trasie wyniosła 80 km/h. O ile krótszy był czas przejazdu tej drogi samochodem osobowym od czasu przejazdu busem?
/Szkoła podstawowa
Motocykl przebył drogę 180 km w czasie 120 minut. Prędkość średnia samochodu osobowego na tej samej trasie wyniosła 72 km/h. O ile krótszy był czas przejazdu tej drogi motocyklem od czasu przejazdu samochodem osobowym?
Agata postanowiła przygotować kartkę okolicznościową w kształcie prostokąta, ozdobioną wzorem dokładnie takim, jak przedstawiony na rysunku. Kartka ta będzie miała wymiary 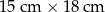 . Do jej ozdobienia Agata chce użyć jednakowych kwadratów, których bok wyraża się całkowitą liczbą centymetrów. Niektóre z tych kwadratów będzie musiała przeciąć na dwie lub na cztery jednakowe części.
. Do jej ozdobienia Agata chce użyć jednakowych kwadratów, których bok wyraża się całkowitą liczbą centymetrów. Niektóre z tych kwadratów będzie musiała przeciąć na dwie lub na cztery jednakowe części.
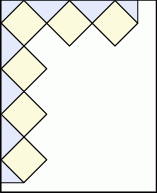
Oblicz maksymalną długość boku jednego kwadratu. Do obliczeń przyjmij przybliżenie 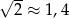 .
.
Karol przykleja na kartce formatu A4 (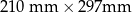 ) kwadraty o boku 2 cm, według wzoru, którego fragment pokazano na rysunku.
) kwadraty o boku 2 cm, według wzoru, którego fragment pokazano na rysunku.
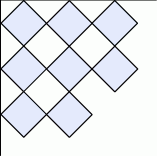
Przekątne każdego kwadratu są równoległe do krawędzi kartki i kwadraty stykają się jednym wierzchołkiem. Oblicz ile maksymalnie takich kwadratów Karol będzie mógł przykleić na kartce. Do obliczeń przyjmij przybliżenie 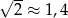 .
.
Prostokątny pasek papieru pocięto na cztery części w sposób przedstawiony na rysunku 1. Z tych części ułożono figurę w kształcie kwadratu tak, jak pokazano na rysunku 2. Pole tego kwadratu jest równe 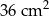 .
.
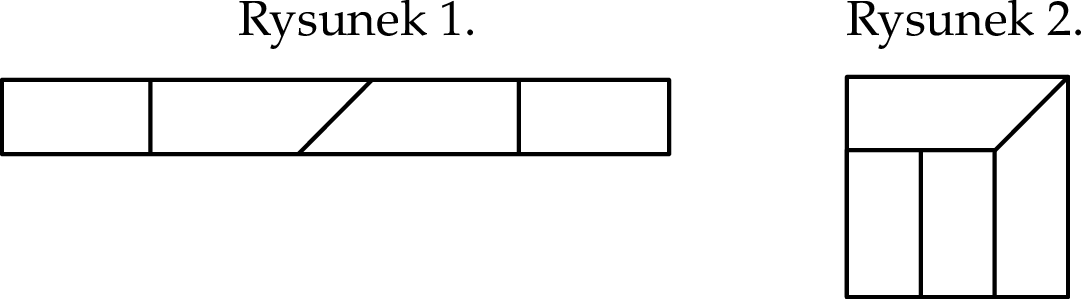
Oblicz obwód paska papieru przed pocięciem.
Liczby 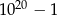 i
i 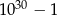 są podzielne przez 41. Uzasadnij, że liczby
są podzielne przez 41. Uzasadnij, że liczby 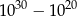 i
i 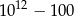 są również podzielne przez 41.
są również podzielne przez 41.
W dwóch naczyniach jest woda. Gdyby z pierwszego naczynia przelano do drugiego 2 litry wody, to w obu naczyniach byłoby jej tyle samo. Gdyby zaś z drugiego do pierwszego przelano 3 litry wody, to w pierwszym naczyniu byłoby jej sześć razy więcej niż w drugim. Ile jest wody w obu naczyniach?
W pierwszym zbiorniku było cztery razy więcej litrów wody niż w drugim. Do każdego zbiornika wlano po 6 litrów wody. Teraz w pierwszym zbiorniku jest dwa razy więcej litrów wody niż w drugim zbiorniku. Oblicz, ile łącznie litrów wody jest w obu zbiornikach.
Pole powierzchni całkowitej prostopadłościanu jest równe 198. Stosunki długości krawędzi prostopadłościanu wychodzących z tego samego wierzchołka prostopadłościanu to 1 : 2 : 3. Oblicz długość przekątnej tego prostopadłościanu.
W trakcie dziesięciu godzin otwarcia sklepu, właściciel prowadził obserwację liczby klientów, którzy odwiedzili ten sklep. Wynik tej obserwacji przedstawiono na wykresie.
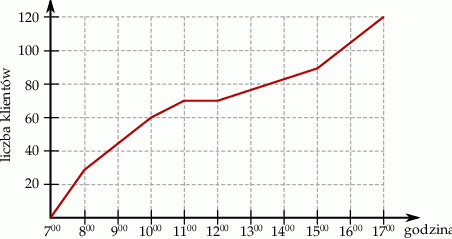
Na podstawie wykresu wybierz zdanie fałszywe.
A) Od
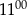 do
do 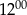 do sklepu nie przyszedł żaden klient.
do sklepu nie przyszedł żaden klient. B) W godzinach od
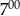 do
do 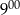 sklep odwiedziło mniej klientów niż od
sklep odwiedziło mniej klientów niż od 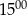 do
do 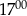 .
. C) W ciągu pierwszej godziny sklep odwiedziło więcej klientów niż w ciągu drugiej godziny.
D) W ciągu trzech pierwszych godzin pracy sklep odwiedziło tylu samo klientów, co w ciągu pozostałych godzin pracy.
W trakcie dziesięciu godzin otwarcia sklepu, właściciel prowadził obserwację liczby klientów, którzy odwiedzili ten sklep. Wynik tej obserwacji przedstawiono na wykresie.
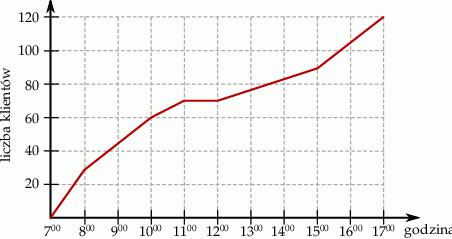
Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Średnio w ciągu jednej godziny obserwacji sklep odwiedzało 12 klientów. | P | F |
| Gdyby właściciel zakończył obserwację po 8 godzinach to średnia liczba klientów w ciągu godziny byłaby wyższa. | P | F |
Każdy bok pięciokąta foremnego 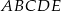 podzielono na 3 równe części i połączono kolejno punkty podziału, w wyniku czego otrzymano dziesięciokąt (rysunek).
podzielono na 3 równe części i połączono kolejno punkty podziału, w wyniku czego otrzymano dziesięciokąt (rysunek).
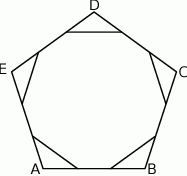
Które z poniższych zdań jest prawdziwe?
A) Dziesięciokąt jest foremny.
B) Wszystkie boki dziesięciokąta mają taką samą długość.
C) Każdy kąt wewnętrzny dziesięciokąta ma miarę 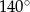 .
.
D) Obwód dziesięciokąta jest mniejszy od obwodu pięciokąta 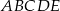 .
.
Z 36 identycznych plastikowych sześcianów o krawędzi długości 1 cm zbudowano graniastosłup prawidłowy czworokątny. Jakie jest największe możliwe pole powierzchni tego graniastosłupa? Zapisz obliczenia.
Na wysokości 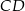 trójkąta równobocznego
trójkąta równobocznego 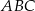 o boku długości 4 zbudowano kwadrat
o boku długości 4 zbudowano kwadrat 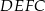 .
.
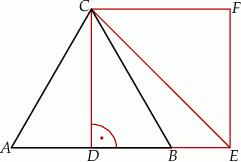
Pole trójkąta 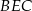 jest równe
jest równe
A) 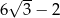 B)
B) 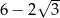 C)
C) 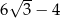 D)
D) 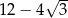
Trzej właściciele firmy – Adam, Janusz i Oskar – kupili samochód dostawczy za kwotę 154 000 zł. Kwoty wpłacone przez Adama, Janusza i Oskara są – odpowiednio – w stosunku 2 : 3 : 6. Jaką kwotę wpłacił Janusz?
A) 14 000 zł B) 28 000 zł C) 42 000 zł D) 84 000 zł
Trzy koleżanki - Kasia, Ala i Oliwia złożyły się na prezent urodzinowy dla ich wspólnego kolegi Kacpra. Prezent kosztował 225 zł, a kwoty wpłacone przez Kasię, Alę i Oliwię są – odpowiednio – w stosunku 4 : 5 : 6. Jaką kwotę wpłaciła Ala?
A) 60 zł B) 75 zł C) 45 zł D) 90 zł
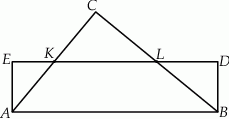
Na rysunku przedstawiono prostokąt 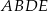 i trójkąt
i trójkąt 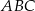 . Punkty
. Punkty 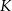 i
i 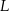 dzielą odcinki
dzielą odcinki 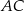 i
i 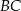 na połowy. Uzasadnij, że pole prostokąta
na połowy. Uzasadnij, że pole prostokąta 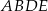 jest równe polu trójkąta
jest równe polu trójkąta 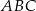 .
.
Która równość jest fałszywa?
A) 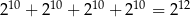 B)
B) 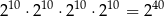
C) 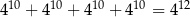 D)
D) 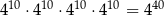
Która równość jest fałszywa?
A) 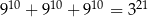 B)
B) 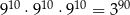
C) 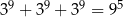 D)
D) 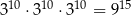
W cukierni Lukier drożdżówka jest o 2 zł tańsza od jagodzianki i o 1 zł droższa od pączka. Za 7 pączków, 3 drożdżówki i 6 jagodzianek zapłacono w tej cukierni 109 zł. Oblicz, ile kosztuje jeden pączek w cukierni Lukier.
Zaokrąglenie ułamka okresowego 9,2(6) z dokładnością do 0,001 jest równe
A) 9,262 B) 9,263 C) 9,266 D) 9,267
Zaokrąglenie ułamka okresowego 3,5(4) z dokładnością do 0,001 jest równe
A) 3,543 B) 3,545 C) 3,544 D) 3,546
Odległość dwóch liczb na osi liczbowej jest równa 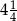 . Mniejsza z tych liczb jest równa
. Mniejsza z tych liczb jest równa 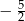 . Większa z tych liczb jest równa
. Większa z tych liczb jest równa
A) 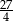 B)
B)  C)
C) 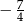 D)
D) 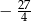
Odległość dwóch liczb na osi liczbowej jest równa 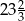 . Jeżeli mniejsza z tych liczb jest równa
. Jeżeli mniejsza z tych liczb jest równa 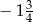 , to większa z tych liczb jest równa
, to większa z tych liczb jest równa
A) 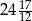 B)
B) 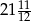 C)
C) 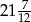 D)
D) 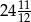
Odległość dwóch liczb na osi liczbowej jest równa 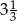 . Mniejsza z tych liczb jest równa
. Mniejsza z tych liczb jest równa 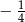 . Większa z tych liczb jest równa
. Większa z tych liczb jest równa
A) 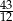 B)
B) 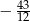 C)
C) 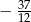 D)
D) 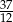
Oprocentowanie kredytu hipotecznego w pewnym banku, które dotychczas wynosiło 6%, wzrosło o 3 punkty procentowe. Zatem oprocentowanie tego kredytu wzrosło o
A) 3% B) 25% C) 50% D) 9%
Oprocentowanie kredytu hipotecznego w pewnym banku, które dotychczas wynosiło 16%, zmalało o 4 punkty procentowe. Zatem oprocentowanie tego kredytu zmalało o
A) 3% B) 25% C) 50% D) 9%
Oprocentowanie kredytu w banku wynosiło 15%. Bank podwyższył oprocentowanie kredytu o 3 punkty procentowe. O ile procent zostało zwiększone oprocentowanie tego kredytu?
A) 20% B) 18% C) 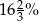 D) 12%
D) 12%
W pewnym banku prowizja od udzielanych kredytów hipotecznych przez cały styczeń była równa 4%. Na początku lutego ten bank obniżył wysokość prowizji od wszystkich kredytów o 1 punkt procentowy. Oznacza to, że prowizja od kredytów hipotecznych w tym banku zmniejszyła się o
A) 1% B) 25% C) 33% D) 75%
Wyrażenie 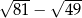 jest równe A/B.
jest równe A/B.
A) 2 B) 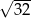
Wyrażenie 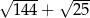 jest równe C/D.
jest równe C/D.
C) 13 D) 17
Wyrażenie 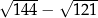 jest równe A/B.
jest równe A/B.
A) 2 B) 1
Wyrażenie 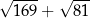 jest równe C/D.
jest równe C/D.
C) 22 D) 23
W pewnej klasie liczba dziewcząt stanowi 60% liczby osób w tej klasie. Gdy 6 dziewcząt wyjechało na mecz siatkówki, w klasie pozostało tyle samo chłopców, ile dziewcząt. Oblicz, ile osób liczy ta klasa oraz ilu jest w niej chłopców.
W pewnej klasie liczba dziewcząt stanowi 60% liczby wszystkich uczniów. Gdyby 6 dziewcząt przeniosło się do innej klasy, w klasie pozostałoby po tyle samo dziewcząt i chłopców. Oblicz ile osób liczy ta klasa oraz ile jest w niej chłopców.
W pewnej klasie liczba chłopców stanowi 60% liczby wszystkich uczniów. Gdyby 6 chłopców przeniosło się do innej klasy, w klasie pozostałoby po tyle samo dziewcząt i chłopców. Oblicz ile osób liczy ta klasa oraz ile jest w niej dziewcząt.
W pewnej klasie liczba chłopców stanowi 75% liczby dziewcząt. Gdyby do tej klasy doszło jeszcze czterech chłopców, to liczba chłopców byłaby równa liczbie dziewcząt. Ile dziewcząt jest w tej klasie? Zapisz obliczenia.
W pewnej klasie liczba chłopców stanowi 80% liczby dziewcząt. Gdyby do tej klasy doszło jeszcze trzech chłopców, to liczba chłopców byłaby równa liczbie dziewcząt. Ile dziewcząt jest w tej klasie? Zapisz obliczenia.
Na rysunku przedstawiono wzór jaki został naniesiony na prostokąt 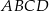 . Wzór ten składa się z 7 prostokątów o bokach
. Wzór ten składa się z 7 prostokątów o bokach  i
i 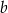 .
.
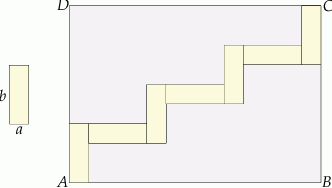
Pole prostokąta 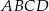 jest równe
jest równe
A) 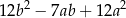 B)
B) 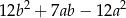 C)
C) 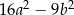 D)
D)