Oblicz średnicę koła o polu 1.
/Szkoła podstawowa
Oblicz średnicę koła o polu 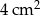 .
.
Oblicz średnicę koła o polu 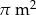 .
.
Oblicz średnicę koła o polu 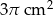 .
.
Wypisano ułamki spełniające łącznie następujące warunki:
-
mianownik każdego z nich jest równy 4,
-
licznik każdego z nich jest liczbą naturalną większą od mianownika,
-
każdy z tych ułamków jest większy od liczby 3 oraz mniejszy od liczby 5.
Wszystkich ułamków spełniających powyższe warunki jest
A) sześć B) siedem C) osiem D) dziewięć
W pewnym rombie jeden z kątów wewnętrznych ma miarę 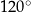 . Obwód tego rombu jest równy 24 cm. Dłuższa przekątna tego rombu ma długość
. Obwód tego rombu jest równy 24 cm. Dłuższa przekątna tego rombu ma długość
A) 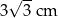 B) 6 cm C)
B) 6 cm C) 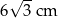 D) 12 cm
D) 12 cm
W pewnym rombie jeden z kątów wewnętrznych ma miarę 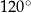 . Obwód tego rombu jest równy 28 cm. Dłuższa przekątna tego rombu ma długość
. Obwód tego rombu jest równy 28 cm. Dłuższa przekątna tego rombu ma długość
A) 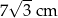 B) 7 cm C)
B) 7 cm C) 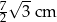 D) 14 cm
D) 14 cm
W kwiaciarni było trzy razy więcej czerwonych róż niż białych. Pan Nowak kupił 40 czerwonych róż i wtedy w kwiaciarni zostało dwa razy więcej białych róż niż czerwonych. Ile białych róż było w kwiaciarni?
Kamil miał cukierki w dwóch smakach – orzechowe i miętowe. Początkowo cukierków o smaku orzechowym było cztery razy więcej niż cukierków o smaku miętowym. Gdy Kamil zjadł 21 cukierków orzechowych, to okazało się, że cukierków miętowych jest dwa razy więcej niż orzechowych. Ile cukierków miętowych miał Kamil?
Oblicz miarę kąta  .
.
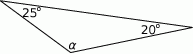
Oblicz miarę kąta  .
.

Oblicz miarę kąta  .
.

Wykaż, że jeżeli 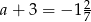 i
i 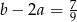 , to wartość wyrażenia
, to wartość wyrażenia 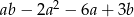 jest równa
jest równa  .
.
Trójkąt 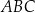 jest trójkątem równobocznym o boku długości 2. Obszar
jest trójkątem równobocznym o boku długości 2. Obszar  jest zawarty między półokręgiem o średnicy
jest zawarty między półokręgiem o średnicy 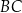 i łukiem okręgu o środku
i łukiem okręgu o środku 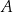 przechodzącym przez punkty
przechodzącym przez punkty 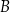 i
i 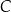 . Oblicz pole obszaru
. Oblicz pole obszaru 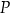 .
.
W koszu znajduje się 6 jabłek zielonych, 8 czerwonych i 4 żółte. Joasia z zawiązanymi oczami wyjmuje jabłka z kosza. Ile co najmniej jabłek powinna wyjąć, aby mieć pewność, że wyjęła przynajmniej jedno czerwone jabłko?
A) 8 B) 10 C) 11 D) 17
W sali teatralnej znajduje się 20 rzędów siedzeń, przy czym w każdym z rzędów jest 25 miejsc.
Ile co najmniej osób musi być na widowni, aby mieć pewność, że przynajmniej w jednym z rzędów zajęte zostały wszystkie miejsca?
A) 25 B) 480 C) 481 D) 44
Przedstaw ułamek okresowy 0,3(12) jako ułamek zwykły.
Przedstaw ułamek okresowy 0,(21) jako ułamek zwykły.
Przedstaw ułamek okresowy 0,(145) jako ułamek zwykły.
Przedstaw ułamek okresowy 0,7(3) jako ułamek zwykły.
W wycieczce szkolnej wzięło udział 12 dziewcząt i 8 chłopców z klasy Va, 13 chłopców i 11 dziewcząt z klasy Vb oraz czworo nauczycieli. Prawdopodobieństwo, że losowo wybrany uczestnik wycieczki jest chłopcem z klasy Va, jest równe
A)  B)
B) 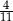 C)
C) 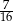 D)
D) 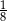
Zestaw lutowniczy składa się z lutownicy, 6 końcówek lutowniczych, 5 narzędzi lutowniczych oraz 2 pincet. W A/B zestawach lutowniczych znajduje się 1368 końcówek lutowniczych.
A) 228 B) 171
Największa liczba zestawów lutowniczych, które można skompletować z: 95 lutownic, 442 końcówek lutowniczych, 357 narzędzi lutowniczych i 147 pincet, jest równa C/D.
C) 71 D) 73
Do zbiornika wypełnionego w 65% wodą dolano 12 litrów wody. Teraz woda wypełnia 80% pojemności zbiornika. Ile litrów wody jest teraz w zbiorniku?
A) 52 litry B) 64 litry C) 77 litrów D) 80 litrów
Cena towaru wzrosła z 1200 zł do 1248 zł. O jaki procent wzrosła cena?
A) 40% B) 4% C) 0,4% D) 0,04%
Tata Karola zainwestował w waluty elektroniczne i za 480 zł kupił bitmonety. Po pół roku sprzedał kupione bitmonety za 1 920 zł. Wartość bitmonet od momentu ich zakupu do momentu sprzedaży
A) wzrosła o 500%. B) wzrosła o 400%. C) wzrosła o 300%. D) wzrosła o 200%.
Maja grała z przyjaciółmi w ekonomiczną grę strategiczną. W trakcie tej gry zainwestowała w zakup nieruchomości 56 tys. gambitów – wirtualnych monet. Po upływie 30 minut odsprzedała tę nieruchomość za 280 tys. gambitów. Wartość nieruchomości od momentu jej zakupienia do momentu sprzedaży
A) wzrosła o 500%. B) wzrosła o 400%. C) wzrosła o 80%. D) wzrosła o 20%.
Program komputerowy kosztował tydzień temu 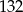 zł, niestety jego cena wzrosła o
zł, niestety jego cena wzrosła o 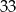 zł. O ile procent zdrożał ten program?
zł. O ile procent zdrożał ten program?
A) o 15% B) o 5% C) o 99% D) o 25%
Punkt kratowy to miejsce przecięcia się linii kwadratowej siatki. Pole wielokąta, którego wierzchołki znajdują się w punktach kratowych kwadratowej siatki na płaszczyźnie, można obliczyć ze wzoru Picka:
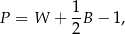
gdzie 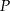 oznacza pole wielokąta,
oznacza pole wielokąta, 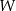 – liczbę punktów kratowych leżących wewnątrz wielokąta, a
– liczbę punktów kratowych leżących wewnątrz wielokąta, a 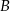 – liczbę punktów kratowych leżących na brzegu tego wielokąta.
– liczbę punktów kratowych leżących na brzegu tego wielokąta.
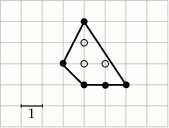
W wielokącie przedstawionym na rysunku 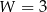 oraz
oraz 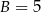 , zatem
, zatem 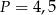 .
.
Wewnątrz pewnego wielokąta znajduje się 5 punktów kratowych, a na jego brzegu jest 6 punktów kratowych. Pole tego wielokąta jest równe
A) 6 B) 6,5 C) 7 D) 7,5
Punkt kratowy to miejsce przecięcia się linii kwadratowej siatki. Pole wielokąta, którego wierzchołki znajdują się w punktach kratowych kwadratowej siatki na płaszczyźnie, można obliczyć ze wzoru Picka:
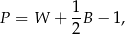
gdzie 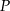 oznacza pole wielokąta,
oznacza pole wielokąta, 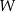 – liczbę punktów kratowych leżących wewnątrz wielokąta, a
– liczbę punktów kratowych leżących wewnątrz wielokąta, a 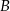 – liczbę punktów kratowych leżących na brzegu tego wielokąta.
– liczbę punktów kratowych leżących na brzegu tego wielokąta.
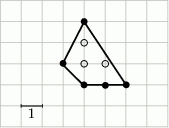
W wielokącie przedstawionym na rysunku 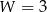 oraz
oraz 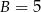 , zatem
, zatem 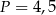 .
.
Wielokąt, którego pole jest równe 15, może mieć A/B punktów kratowych leżących na brzegu wielokąta.
A) 7 B) 8
Pole wielokąta, który ma dwukrotnie więcej punktów kratowych leżących na brzegu wielokąta niż punktów leżących wewnątrz, wyraża się liczbą C/D.
C) parzystą D) nieparzystą
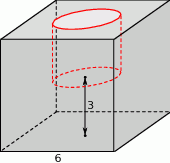
W sześcianie o krawędzi podstawy 6 wydrążono pionowy walec, którego wysokość i średnica są równe połowie długości krawędzi sześcianu. Oblicz pole powierzchni całkowitej tej bryły.
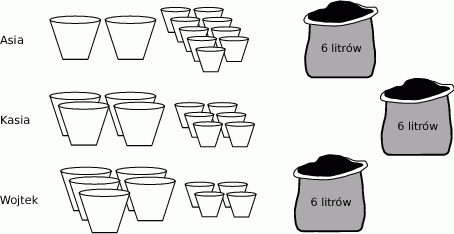
Asia, Kasia i Wojtek przesadzają kwiatki do doniczek. Każde z nich ma 6-litrowy worek ziemi ogrodniczej i doniczki dwóch wielkości. Asia wykorzystała całą ziemię, którą dysponowała, i napełniła 2 duże doniczki i 9 małych. Kasia całą swoją ziemię zużyła do wypełnienia 4 dużych i 6 małych doniczek. Wojtek chciałby wypełnić ziemią 5 dużych i 4 małe doniczki. Czy wystarczy mu ziemi, którą ma w worku? Uzasadnij odpowiedź.
Olaf, Marysia i Kamil przygotowują farbę do pomalowania swoich pokojów. Każde z nich potrzebuje 12 litrów farby i każde z nich miesza ze sobą dwa rodzaje farby: białą, która jest dostępna w większych puszkach i granatową, która jest dostępna w mniejszych puszkach. Olaf przygotował 12 litrów farby mieszając farbę z 6 dużych puszek i 4 małych, a Marysia przygotowała tę samą ilość farby mieszając farbę z 5 dużych i 6 małych puszek. Kamil chce przygotować swoją farbę używając 7 dużych puszek i jednej małej. Czy wystarczy mu farby do pomalowania pokoju? Uzasadnij odpowiedź.

Ile ścian bocznych ma graniastosłup o 14 wierzchołkach?
Czy w każdym graniastosłupie prawidłowym wszystkie przekątne mają tę samą długość?
Ile ścian bocznych ma graniastosłup o 100 wierzchołkach?
Czy graniastosłup może mieć 10 ścian bocznych i 20 wierzchołków?
Czy graniastosłup może mieć 20 krawędzi?
Czy istnieje graniastosłup, który nie ma przekątnych?
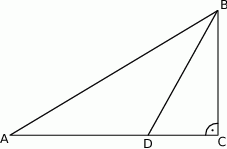
Dwusieczna kąta ostrego 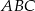 przecina przyprostokątną
przecina przyprostokątną 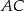 trójkąta prostokątnego
trójkąta prostokątnego  w punkcie
w punkcie 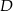 .
.
Udowodnij, że jeżeli 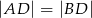 , to
, to 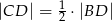 .
.
Dwusieczna kąta ostrego 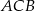 przecina przyprostokątną
przecina przyprostokątną 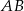 trójkąta prostokątnego
trójkąta prostokątnego 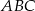 w punkcie
w punkcie 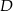 .
.
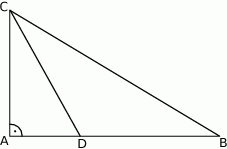
Udowodnij, że jeżeli 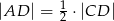 , to
, to 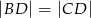 .
.
Wartość wyrażenia 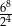 jest równa
jest równa
A) 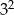 B)
B) 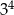 C)
C) 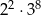 D)
D) 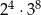
Wartość wyrażenia 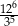 jest równa
jest równa
A) 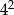 B)
B) 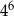 C)
C) 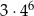 D)
D) 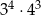
W ciągu dwóch godzin trzy jednakowe maszyny produkują razem 1200 guzików. Ile guzików wyprodukuje pięć takich maszyn w ciągu jednej godziny? Przyjmij, że maszyny pracują z taką samą, stałą wydajnością.
A) 800 B) 900 C) 1000 D) 1500
W ciągu trzech godzin dwie jednakowe maszyny produkują razem 1200 guzików. Ile guzików wyprodukuje pięć takich maszyn w ciągu dwóch godzin? Przyjmij, że maszyny pracują z taką samą, stałą wydajnością.
A) 2000 B) 900 C) 1000 D) 1500

