Wyznacz wszystkie liczby całkowite  , dla których liczba
, dla których liczba 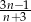 jest liczbą całkowitą.
jest liczbą całkowitą.
/Szkoła średnia/Liczby/Liczby całkowite
Liczby naturalne dodatnie 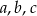 spełniają równanie
spełniają równanie 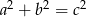 . Uzasadnij, że liczba
. Uzasadnij, że liczba 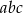 jest
jest
- parzysta;
- podzielna przez 3.
Udowodnij, że różnica sześcianów dwóch kolejnych liczb całkowitych nie jest liczbą podzielną przez 5.
Wykaż, że dla każdej liczby naturalnej 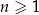 liczba
liczba 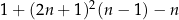 jest podzielna przez 24.
jest podzielna przez 24.
Wykaż, że suma pięciu kolejnych liczb naturalnych nie może być liczbą pierwszą.
Uzasadnij, że liczba 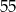 jest dzielnikiem liczby 31!, i że liczba 37 nie jest dzielnikiem liczby 31!.
jest dzielnikiem liczby 31!, i że liczba 37 nie jest dzielnikiem liczby 31!.
Wykaż, że dla każdej liczby całkowitej  liczba
liczba 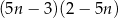 przy dzieleniu przez 25 daje resztę 19.
przy dzieleniu przez 25 daje resztę 19.
Wykaż, że liczba 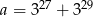 jest podzielna przez 30.
jest podzielna przez 30.
Wykaż, że liczba 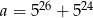 jest podzielna przez 130.
jest podzielna przez 130.
Wykaż, że suma sześcianów trzech kolejnych liczb naturalnych parzystych jest podzielna przez 24.
Wykaż, że suma sześcianów trzech kolejnych liczb naturalnych nieparzystych jest podzielna przez 3.
Liczba  z dzielenia przez 4 daje resztę 1. Liczba
z dzielenia przez 4 daje resztę 1. Liczba 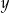 z dzielenia przez 4 daje resztę 3. Wyznacz resztę z dzielenia liczby
z dzielenia przez 4 daje resztę 3. Wyznacz resztę z dzielenia liczby 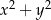 przez 8.
przez 8.
Niech 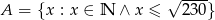 i
i 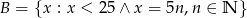 . Wyznacz zbiory
. Wyznacz zbiory 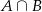 oraz
oraz 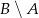 .
.
Dla jakich cyfr  i
i 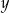
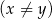 liczba
liczba 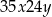 jest podzielna przez 45? (
jest podzielna przez 45? (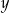 – jest to cyfra jedności, a
– jest to cyfra jedności, a  – cyfra tysięcy).
– cyfra tysięcy).
Wykaż, że dla każdej liczby naturalnej  liczba
liczba 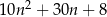 przy dzieleniu przez 5 daje resztę 3.
przy dzieleniu przez 5 daje resztę 3.
Wykaż, że dla każdej liczby całkowitej 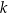 reszta z dzielenia liczby
reszta z dzielenia liczby 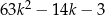 przez 7 jest równa 4.
przez 7 jest równa 4.
Wykaż, że dla każdej liczby całkowitej 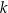 reszta z dzielenia liczby
reszta z dzielenia liczby 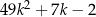 przez 7 jest równa 5.
przez 7 jest równa 5.
Wykaż, że dla każdej liczby całkowitej nieparzystej  liczba
liczba 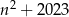 jest podzielna przez 8.
jest podzielna przez 8.
Wykaż, że jeżeli liczba  nie dzieli się przez 3, to liczba
nie dzieli się przez 3, to liczba 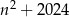 jest podzielna przez 3.
jest podzielna przez 3.
Wykaż, że 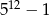 jest liczbą podzielną przez 31.
jest liczbą podzielną przez 31.
Wykaż, że 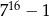 jest liczbą podzielną przez
jest liczbą podzielną przez 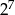 .
.
Wykaż, że 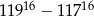 jest liczbą podzielną przez 59.
jest liczbą podzielną przez 59.
Wykaż, że jeżeli  jest liczbą nieparzystą to liczba
jest liczbą nieparzystą to liczba
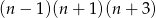
jest liczbą podzielną przez 48.
Dane są liczby całkowite  i
i 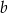 . Wykaż, że jeżeli liczba
. Wykaż, że jeżeli liczba 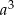 jest podzielna przez
jest podzielna przez  , to liczba
, to liczba 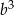 też jest podzielna
też jest podzielna 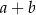 .
.
Wykaż, że liczba 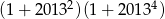 jest dzielnikiem liczby
jest dzielnikiem liczby
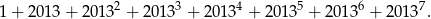
Wykaż, że liczba 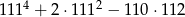 jest dzielnikiem liczby
jest dzielnikiem liczby
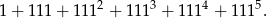
Wykaż, że liczba 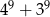 jest podzielna przez 91.
jest podzielna przez 91.
Wykaż, że liczba 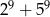 jest podzielna przez 133.
jest podzielna przez 133.
Uzasadnij, że suma trzech kolejnych potęg liczby 2 o wykładnikach całkowitych dodatnich jest podzielna przez 14.

