Wykaż, że dla dowolnej liczby całkowitej 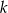 różnica iloczynu tej liczby i liczby od niej o 3 większej oraz iloczynu dwóch kolejnych liczb całkowitych większych od
różnica iloczynu tej liczby i liczby od niej o 3 większej oraz iloczynu dwóch kolejnych liczb całkowitych większych od 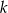 jest równa -2.
jest równa -2.
/Szkoła średnia/Liczby/Liczby całkowite
Udowodnij, że dla każdej liczby całkowitej 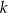 i dla każdej liczby całkowitej
i dla każdej liczby całkowitej 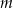 liczba
liczba 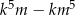 jest podzielna przez 10.
jest podzielna przez 10.
Wykaż, że dla każdej liczby naturalnej  liczba
liczba 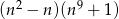 jest podzielna przez 6.
jest podzielna przez 6.
Udowodnij, że po wymnożeniu kolejnych liczb naturalnych od 1 do 30, czyli po wykonaniu działania 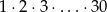 , otrzymamy liczbę, która kończy się dokładnie 7 zerami.
, otrzymamy liczbę, która kończy się dokładnie 7 zerami.
Wykaż, że jeśli  jest liczbą nieparzystą, to liczba
jest liczbą nieparzystą, to liczba 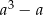 jest podzielna przez 12.
jest podzielna przez 12.
Wykaż, że dla każdej liczby naturalnej 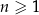 liczba
liczba 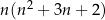 jest podzielna przez 6.
jest podzielna przez 6.
Wykaż, że dla każdej liczby naturalnej 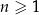 liczba
liczba 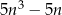 jest podzielna przez 30.
jest podzielna przez 30.
Wykaż, że dla każdej liczby całkowitej  liczba
liczba 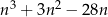 jest podzielna przez 6.
jest podzielna przez 6.
Udowodnij, że dla każdej liczby nieparzystej  wyrażenie
wyrażenie 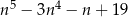 jest podzielne przez 16.
jest podzielne przez 16.
Udowodnij, że dla każdej liczby nieparzystej  wyrażenie
wyrażenie 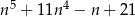 jest podzielne przez 16.
jest podzielne przez 16.
Uzasadnij, że dla każdej dodatniej liczby całkowitej  liczba
liczba 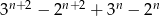 jest wielokrotnością liczby 10.
jest wielokrotnością liczby 10.
Wykaż, że liczba 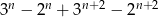 jest podzielna przez 10,
jest podzielna przez 10, 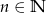 .
.
Wykaż, że jeśli 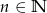 , to liczba
, to liczba 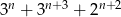 jest podzielna przez 4.
jest podzielna przez 4.
Udowodnij, że dla każdej liczby naturalnej  , gdzie
, gdzie 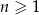 , liczba
, liczba 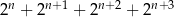 jest podzielna przez 30.
jest podzielna przez 30.
Uzasadnij, że dla każdej liczby całkowitej 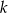 liczba
liczba 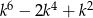 jest podzielna przez 36.
jest podzielna przez 36.
Wykaż, że jeżeli 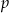 jest liczbą pierwszą większą od 3 to
jest liczbą pierwszą większą od 3 to 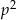 przy dzieleniu przez 24 daje resztę 1.
przy dzieleniu przez 24 daje resztę 1.
Uzasadnij, że równanie 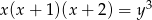 nie ma rozwiązań w liczbach całkowitych dodatnich
nie ma rozwiązań w liczbach całkowitych dodatnich 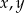 .
.
Udowodnij, że dla każdej liczby całkowitej 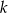 i dla każdej liczby całkowitej
i dla każdej liczby całkowitej 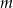 liczba
liczba 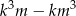 jest podzielna przez 6.
jest podzielna przez 6.
Udowodnij, że dla każdej liczby całkowitej 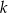 i dla każdej liczby całkowitej
i dla każdej liczby całkowitej 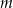 liczba
liczba 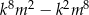 jest podzielna przez 36.
jest podzielna przez 36.
Niech 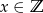 . Wykaż, że wyrażenie
. Wykaż, że wyrażenie 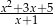 przyjmuje wartość całkowitą tylko dla czterech wartości
przyjmuje wartość całkowitą tylko dla czterech wartości  . Podaj te liczby.
. Podaj te liczby.
Wykaż, że dla każdej liczby naturalnej  liczba
liczba 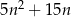 jest podzielna przez 10.
jest podzielna przez 10.
Wykaż, że dla każdej liczby naturalnej 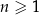 liczba
liczba 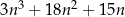 jest podzielna przez 6.
jest podzielna przez 6.
Wykaż, że dla każdej liczby naturalnej 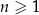 liczba
liczba 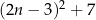 jest podzielna przez 8.
jest podzielna przez 8.
Wykaż, że dla każdej liczby naturalnej 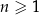 liczba
liczba 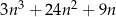 jest podzielna przez 6.
jest podzielna przez 6.
Wykaż, że dla każdej liczby naturalnej  liczba
liczba 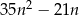 jest podzielna przez 14.
jest podzielna przez 14.
Wykaż, że dla każdej liczby naturalnej 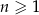 liczba
liczba 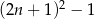 jest podzielna przez 8.
jest podzielna przez 8.
Wykaż, że liczba 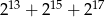 jest podzielna przez 21.
jest podzielna przez 21.
Wykaż, że liczba 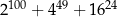 jest podzielna przez 21.
jest podzielna przez 21.
Uzasadnij, że liczba 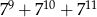 jest podzielna przez 399.
jest podzielna przez 399.
Udowodnij, że liczba 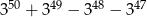 jest podzielna przez 32.
jest podzielna przez 32.
Wykaż, że liczba 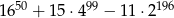 jest podzielna przez 13.
jest podzielna przez 13.
Wykaż, że liczba 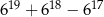 jest podzielna przez 82.
jest podzielna przez 82.
Wykaż, że liczba 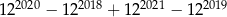 jest podzielna przez 429.
jest podzielna przez 429.
Wykaż, że liczba 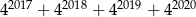 jest podzielna przez 17.
jest podzielna przez 17.
Wykaż, że liczba 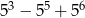 jest podzielna przez 101.
jest podzielna przez 101.
Udowodnij, że liczba 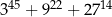 jest podzielna przez 37.
jest podzielna przez 37.
Wykaż, że liczba 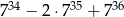 jest podzielna przez 12.
jest podzielna przez 12.
Wykaż, że liczba 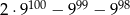 jest podzielna przez 8.
jest podzielna przez 8.
Udowodnij, że liczba 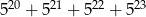 jest podzielna przez 13.
jest podzielna przez 13.
Wykaż, że liczba 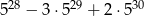 jest podzielna przez 18.
jest podzielna przez 18.
Uzasadnij, że liczba 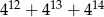 jest podzielna przez 42.
jest podzielna przez 42.
Wykaż, że liczba 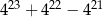 jest podzielna przez 38.
jest podzielna przez 38.
Wykaż, że liczba 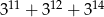 jest podzielna przez 31.
jest podzielna przez 31.
Wykaż, że liczba 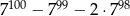 jest podzielna przez 4.
jest podzielna przez 4.
Wykaż, że liczba 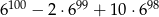 jest podzielna przez 17.
jest podzielna przez 17.
Udowodnij, że liczba 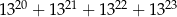 jest podzielna przez 35.
jest podzielna przez 35.
Wykaż, że dla dowolnych liczb całkowitych 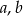 liczba
liczba 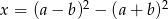 jest podzielna przez 4.
jest podzielna przez 4.
Wykaż, że dla dowolnych liczb całkowitych 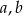 liczba
liczba 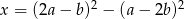 jest podzielna przez 3.
jest podzielna przez 3.
Wykaż, że kwadrat liczby całkowitej dającej z dzielenia przez 3 resztę 2, przy dzieleniu przez 3 daje resztę 1.
Uzasadnij, że jeżeli liczba całkowita nie dzieli się przez 3, to jej kwadrat przy dzieleniu przez 3 daje resztę 1.
Uzasadnij, że jeżeli liczba całkowita jest nieparzysta, to jej kwadrat przy dzieleniu przez 8 daje resztę 1.
Wykaż, że dla każdej liczby naturalnej  reszta z dzielenia liczby
reszta z dzielenia liczby 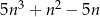 przez
przez 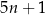 jest równa 1.
jest równa 1.
Rozważmy dwie kolejne liczby naturalne  i
i 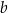 takie, że
takie, że 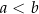 oraz obie są niepodzielne przez 3. Udowodnij, że liczba
oraz obie są niepodzielne przez 3. Udowodnij, że liczba 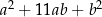 jest podzielna przez 9.
jest podzielna przez 9.
Wykaż, że suma kwadratów trzech liczb całkowitych, które przy dzieleniu przez 3 dają resztę 2 jest podzielna przez 3.
Uzasadnij, że jeżeli  jest liczbą naturalną to liczba
jest liczbą naturalną to liczba 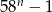 dzieli się przez 19.
dzieli się przez 19.

