Znajdź wszystkie liczby naturalne  takie, że liczba
takie, że liczba 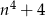 jest liczbą pierwszą.
jest liczbą pierwszą.
/Konkursy/Zadania/Liczby/Całkowite
Pokazać, że dla każdej liczby całkowitej  liczba
liczba 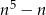 jest podzielna przez 30.
jest podzielna przez 30.
Wyznacz najmniejszą liczbę 4-cyfrową, która przy dzieleniu przez 7 daje resztę 6, a przy dzieleniu przez 6 daje resztę 5.
Niech 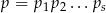 będzie liczbą całkowitą o cyfrach
będzie liczbą całkowitą o cyfrach 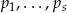 . Pokaż, że
. Pokaż, że
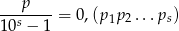
(okresowe rozwinięcie dziesiętne).
Dla jakich liczb całkowitych  liczba
liczba 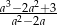 jest także liczbą całkowitą?
jest także liczbą całkowitą?
W liczbie, o której wiadomo, że miała, co najmniej dwie cyfry, wykreślono ostatnią cyfrę. Otrzymana liczba była,  razy mniejsza od poprzedniej. Jaka jest największa możliwa wartość
razy mniejsza od poprzedniej. Jaka jest największa możliwa wartość  ?
?
Czy liczba nieparzysta i połowa następującej po niej liczby parzystej mogą mieć wspólny dzielnik większy niż 1?
Dana jest liczba całkowita 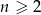 . Niech
. Niech 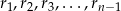 będą odpowiednio resztami z dzielenia liczb
będą odpowiednio resztami z dzielenia liczb
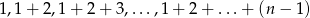
przez  . Znaleźć wszystkie takie wartości
. Znaleźć wszystkie takie wartości  , że ciąg
, że ciąg 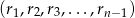 jest permutacją ciągu
jest permutacją ciągu 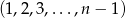 .
.
Dane są różne liczby pierwsze 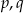 oraz takie dodatnie liczby całkowite
oraz takie dodatnie liczby całkowite 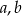 , że liczba
, że liczba 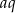 daję resztę 1 przy dzieleniu przez
daję resztę 1 przy dzieleniu przez 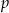 , a liczba
, a liczba 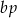 daje resztę 1 przy dzieleniu przez
daje resztę 1 przy dzieleniu przez 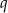 . Wykaż, że
. Wykaż, że
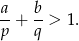
Wyznacz wszystkie liczby pierwsze 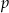 takie, że liczby
takie, że liczby 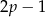 i
i 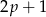 też są liczbami pierwszymi.
też są liczbami pierwszymi.
Udowodnij, że suma sześcianów trzech kolejnych liczb naturalnych jest podzielna przez 9.
Udowodnij, że suma sześcianów trzech kolejnych liczb całkowitych nieparzystych jest podzielna przez 9.
Udowodnij, że suma sześcianów trzech kolejnych liczb całkowitych niepodzielnych przez 4 jest liczbą podzielną przez 36.
Pokazać, że dla każdej liczby całkowitej  liczba
liczba 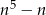 jest podzielna przez 5.
jest podzielna przez 5.
Wykaż, że dla każdej liczby całkowitej  liczba
liczba 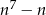 jest podzielna przez 7.
jest podzielna przez 7.
Ile cyfr ma w zapisie dziesiętnym liczba 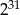 ?
?

