Pole ściany bocznej ostrosłupa prawidłowego czworokątnego jest równe 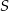 . Kąt płaski przy wierzchołku ostrosłupa ma miarę
. Kąt płaski przy wierzchołku ostrosłupa ma miarę 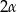 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
/Szkoła średnia/Geometria/Stereometria/Ostrosłup
Wykaż, że jeśli wszystkie krawędzie boczne ostrosłupa trójkątnego tworzą z podstawą kąty o równych miarach to spodek wysokości ostrosłupa jest środkiem okręgu opisanego na tym trójkącie.
Podstawą ostrosłupa 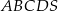 jest prostokąt
jest prostokąt 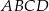 o bokach długości
o bokach długości  i
i 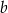 . Krawędź
. Krawędź 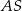 jest prostopadła do płaszczyzny podstawy. Odległość wierzchołka
jest prostopadła do płaszczyzny podstawy. Odległość wierzchołka 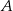 od krawędzi
od krawędzi 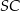 jest równa
jest równa 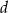 . Wyznacz objętość tego ostrosłupa.
. Wyznacz objętość tego ostrosłupa.
W czworościanie 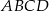 krawędź
krawędź 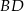 ma długość 2, a wszystkie pozostałe krawędzie mają długość 4.
ma długość 2, a wszystkie pozostałe krawędzie mają długość 4.
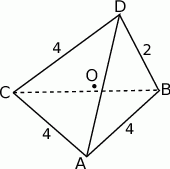
- Oblicz odległość krawędzi
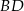 od krawędzi
od krawędzi 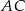 .
. - Wiedząc, że punkt
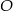 jest równoodległy od wszystkich wierzchołków czworościanu, oblicz długość odcinka
jest równoodległy od wszystkich wierzchołków czworościanu, oblicz długość odcinka 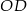 .
.
W ostrosłupie prawidłowym czworokątnym krawędź boczna tworzy z krawędzią podstawy kąta  . Wyznacz cosinus kąta między sąsiednimi ścianami bocznymi.
. Wyznacz cosinus kąta między sąsiednimi ścianami bocznymi.
W sferę o promieniu 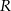 wpisano ostrosłup prawidłowy trójkątny w ten sposób, że wszystkie wierzchołki ostrosłupa leżą na powierzchni sfery. Wiedząc, że krawędź boczna ostrosłupa ma długość 13, a krawędź podstawy długość
wpisano ostrosłup prawidłowy trójkątny w ten sposób, że wszystkie wierzchołki ostrosłupa leżą na powierzchni sfery. Wiedząc, że krawędź boczna ostrosłupa ma długość 13, a krawędź podstawy długość 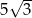 , oblicz
, oblicz 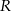 .
.
Krawędź boczna ostrosłupa prawidłowego trójkątnego ma długość 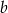 i tworzy z krawędzią podstawy kąt o mierze
i tworzy z krawędzią podstawy kąt o mierze  . Jaką objętość ma ten ostrosłup?
. Jaką objętość ma ten ostrosłup?
W ostrosłupie prawidłowym czworokątnym ściana boczna jest nachylona do płaszczyzny podstawy pod kątem 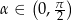 , a krawędź podstawy ma długość
, a krawędź podstawy ma długość  . Przez krawędź podstawy poprowadzono płaszczyznę tworzącą z płaszczyzna podstawy kąt
. Przez krawędź podstawy poprowadzono płaszczyznę tworzącą z płaszczyzna podstawy kąt 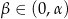 . Wykaż, że pole otrzymanego przekroju jest równe
. Wykaż, że pole otrzymanego przekroju jest równe
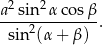
Podstawą ostrosłupa 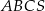 jest trójkąt równoboczny
jest trójkąt równoboczny 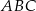 o boku długości 8. Punkt
o boku długości 8. Punkt 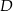 jest środkiem krawędzi
jest środkiem krawędzi 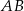 , odcinek
, odcinek 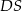 jest wysokością ostrosłupa. Krawędzie
jest wysokością ostrosłupa. Krawędzie 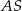 i
i 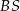 mają długość 7. Oblicz długość krawędzi
mają długość 7. Oblicz długość krawędzi 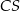 tego ostrosłupa.
tego ostrosłupa.
Podstawą ostrosłupa 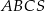 jest trójkąt równoboczny
jest trójkąt równoboczny 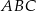 o boku długości 6. Punkt
o boku długości 6. Punkt 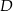 jest środkiem krawędzi
jest środkiem krawędzi 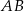 , odcinek
, odcinek 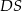 jest wysokością ostrosłupa. Krawędzie
jest wysokością ostrosłupa. Krawędzie 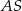 i
i 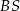 mają długość 8. Oblicz długość krawędzi
mają długość 8. Oblicz długość krawędzi 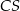 tego ostrosłupa.
tego ostrosłupa.
Podstawą ostrosłupa 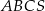 jest trójkąt równoboczny
jest trójkąt równoboczny 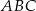 o boku długości 6. Punkt
o boku długości 6. Punkt 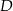 jest środkiem krawędzi
jest środkiem krawędzi 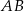 , odcinek
, odcinek 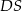 jest wysokością ostrosłupa. Krawędzie
jest wysokością ostrosłupa. Krawędzie 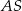 i
i 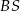 mają długość
mają długość 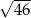 . Oblicz długość krawędzi
. Oblicz długość krawędzi 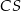 tego ostrosłupa.
tego ostrosłupa.
Podstawą ostrosłupa 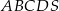 jest czworokąt wypukły
jest czworokąt wypukły 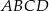 , w którym
, w którym 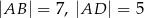 oraz
oraz 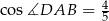 . Każda z krawędzi bocznych ostrosłupa ma długość
. Każda z krawędzi bocznych ostrosłupa ma długość 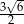 . Oblicz wysokość ostrosłupa.
. Oblicz wysokość ostrosłupa.
Podstawą ostrosłupa 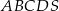 jest czworokąt wypukły
jest czworokąt wypukły 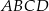 , w którym
, w którym 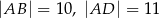 oraz
oraz 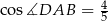 . Każda z krawędzi bocznych ostrosłupa ma długość 6. Oblicz wysokość ostrosłupa.
. Każda z krawędzi bocznych ostrosłupa ma długość 6. Oblicz wysokość ostrosłupa.
Ściany boczne ostrosłupa prawidłowego trójkątnego są trójkątami o przyprostokątnych długości 12 cm. Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.
Podstawą ostrosłupa 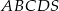 jest romb
jest romb 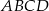 o boku długości 4. Kąt
o boku długości 4. Kąt 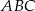 rombu ma miarę
rombu ma miarę 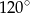 oraz
oraz 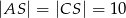 i
i 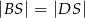 . Oblicz sinus kąta nachylenia krawędzi
. Oblicz sinus kąta nachylenia krawędzi 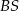 do płaszczyzny podstawy ostrosłupa.
do płaszczyzny podstawy ostrosłupa.
W ostrosłupie prawidłowym czworokątnym 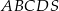 o podstawie
o podstawie 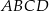 wysokość jest równa
wysokość jest równa 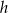 , a kąt między sąsiednimi ścianami bocznymi ostrosłupa ma miarę
, a kąt między sąsiednimi ścianami bocznymi ostrosłupa ma miarę  . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
W ostrosłupie prawidłowym trójkątnym krawędź podstawy ma długość 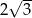 . Oblicz objętość tego ostrosłupa jeżeli ściana boczna jest nachylona do podstawy pod kątem
. Oblicz objętość tego ostrosłupa jeżeli ściana boczna jest nachylona do podstawy pod kątem 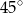 .
.
W ostrosłupie prawidłowym sześciokątnym pole przekroju płaszczyzną przechodzącą przez jego wysokość oraz przez dwie krawędzie boczne jest dwukrotnie większe od pola podstawy i wynosi 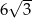 . Oblicz odległość spodka wysokości ostrosłupa od jego krawędzi bocznej.
. Oblicz odległość spodka wysokości ostrosłupa od jego krawędzi bocznej.
Długość krawędzi podstawy ostrosłupa prawidłowego czworokątnego 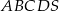 jest równa
jest równa  , a wysokość tego ostrosłupa ma długość
, a wysokość tego ostrosłupa ma długość 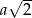 . Punkty
. Punkty 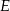 i
i 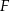 są środkami krawędzi bocznych odpowiednio
są środkami krawędzi bocznych odpowiednio 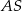 i
i 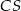 . Oblicz obwód trójkąta
. Oblicz obwód trójkąta 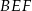 .
.
Podstawą ostrosłupa prawidłowego czworokątnego 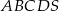 jest kwadrat
jest kwadrat 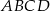 . Pole trójkąta równoramiennego
. Pole trójkąta równoramiennego 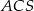 jest równe 120 oraz
jest równe 120 oraz 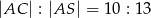 . Oblicz pole powierzchni bocznej tego ostrosłupa.
. Oblicz pole powierzchni bocznej tego ostrosłupa.
W ostrosłup prawidłowy czworokątny wpisano sześcian tak, że jego cztery wierzchołki należą do wysokości ścian bocznych ostrosłupa, a pozostałe do płaszczyzny podstawy. Oblicz stosunek objętości ostrosłupa do objętości sześcianu jeżeli kąt nachylenia ściany bocznej do płaszczyzny podstawy jest równy  .
.
W ostrosłupie 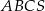 podstawa
podstawa 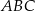 jest trójkątem równobocznym o boku długości
jest trójkątem równobocznym o boku długości  . Krawędź
. Krawędź 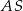 jest prostopadła do płaszczyzny podstawy. Odległość wierzchołka
jest prostopadła do płaszczyzny podstawy. Odległość wierzchołka 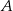 od ściany
od ściany 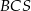 jest równa
jest równa 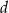 . Wyznacz objętość tego ostrosłupa.
. Wyznacz objętość tego ostrosłupa.
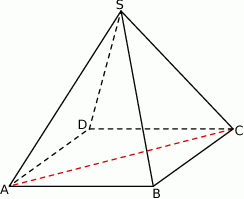
W ostrosłupie prawidłowym czworokątnym 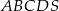 (zobacz rysunek) przekątna
(zobacz rysunek) przekątna 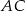 podstawy ma długość
podstawy ma długość 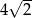 . Kąt
. Kąt 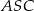 między przeciwległymi krawędziami bocznymi ostrosłupa ma miarę
między przeciwległymi krawędziami bocznymi ostrosłupa ma miarę 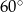 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
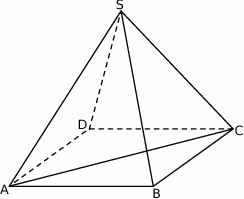
W ostrosłupie prawidłowym czworokątnym 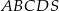 (zobacz rysunek) przekątna
(zobacz rysunek) przekątna 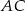 podstawy ma długość 6. Kąt
podstawy ma długość 6. Kąt 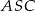 między przeciwległymi krawędziami bocznymi ostrosłupa ma miarę
między przeciwległymi krawędziami bocznymi ostrosłupa ma miarę 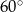 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.