Ostrosłup/Stereometria/Geometria - zadania z matematyki

/Szkoła średnia/Geometria/Stereometria/Ostrosłup

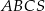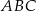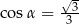Dany jest ostrosłup prawidłowy trójkątny ABCS o podstawie ABC . Krawędź podstawy tego ostrosłupa ma długość . Ściana boczna jest nachylona do płaszczyzny podstawy pod kątem takim, że √ - cos α = --3 3 . Przez środek 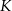krawędzi 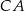i środek 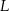krawędzi 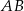poprowadzono płaszczyznę 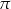prostopadłą do płaszczyzny 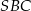SBC . Oblicz pole otrzymanego przekroju.

Dany jest ostrosłup prawidłowy czworokątny 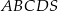ABCDS o podstawie 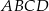ABCD i polu powierzchni bocznej równym 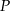. Kąt między wysokościami sąsiednich ścian bocznych poprowadzonych z wierzchołka 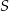ma miarę 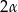. Objętość tego ostrosłupa jest równa 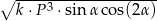∘k -⋅P-3 ⋅-sin-α-cos(2α) , gdzie 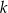jest stałym współczynnikiem liczbowym. Oblicz współczynnik .

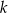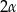W ostrosłup prawidłowy czworokątny wpisano kulę o promieniu . Ściana boczna ostrosłupa nachylona jest do płaszczyzny podstawy pod kątem . Oblicz objętość tego ostrosłupa.

Ukryj Podobne zadania

W ostrosłup prawidłowy czworokątny wpisano kulę o promieniu 2. Ściana boczna ostrosłupa nachylona jest do płaszczyzny podstawy pod kątem 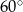60 ∘ . Oblicz objętość tego ostrosłupa.

Oblicz objętość ostrosłupa prawidłowego trójkątnego o krawędzi podstawy 6 cm i krawędzi bocznej 12 cm.

Ukryj Podobne zadania

Oblicz objętość ostrosłupa prawidłowego trójkątnego o krawędzi podstawy długości 6 cm i krawędzi bocznej długości 8 cm.

Każda z krawędzi podstawy trójkątnej ostrosłupa ma długość 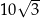√ -- 10 3 , a każda jego krawędź boczna ma długość 15. Oblicz wysokość tego ostrosłupa.

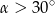W ostrosłupie prawidłowym trójkątnym krawędź podstawy ma długość . Kąt między krawędzią boczną, a krawędzią podstawy ma miarę α > 30∘ . Oblicz objętość ostrosłupa.

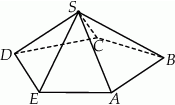
Dany jest ostrosłup o podstawie pięciokątnej 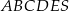ABCDES (zobacz rysunek). Każda ze ścian bocznych tego ostrosłupa jest trójkątem o polu trzy razy mniejszym niż pole pięciokąta 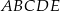ABCDE . Pole powierzchni całkowitej tego ostrosłupa jest równe 136. Oblicz pole jego podstawy.

Krawędź boczna ostrosłupa prawidłowego trójkątnego jest nachylona do płaszczyzny podstawy pod kątem . Przez krawędź podstawy tego ostrosłupa poprowadzono płaszczyznę, która jest nachylona do płaszczyzny podstawy pod katem 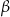, i która przecina przeciwległą krawędź ostrosłupa (zobacz rysunek).

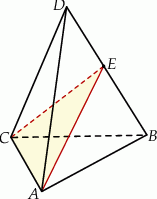
Oblicz stosunek pola powierzchni otrzymanego przekroju do pola powierzchni podstawy ostrosłupa jeżeli wiadomo, że 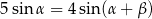5 sinα = 4sin(α + β ) .

Tangens kąta nachylenia ściany bocznej do płaszczyzny podstawy ostrosłupa prawidłowego czworokątnego jest równy . Oblicz tangens nachylenia krawędzi bocznej do płaszczyzny podstawy tego ostrosłupa.

W ostrosłupie prawidłowym trójkątnym 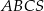ABCS cosinus kąta nachylenia krawędzi bocznej do płaszczyzny podstawy jest równy 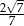√- 2-7- 7 . Wykaż, że pole powierzchni bocznej tego ostrosłupa stanowi 2 3 jego pola powierzchni całkowitej.

Wysokość ostrosłupa prawidłowego sześciokątnego jest równa 6 cm i stanowi długości krawędzi podstawy.

Oblicz miarę kąta nachylenia ściany bocznej do podstawy.
Oblicz objętość ostrosłupa

Ukryj Podobne zadania

Wysokość ostrosłupa prawidłowego sześciokątnego jest równa 9 cm i stanowi długości krawędzi podstawy.

Oblicz miarę kąta nachylenia ściany bocznej do podstawy.
Oblicz objętość ostrosłupa.

W ostrosłupie prawidłowym czworokątnym 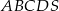ABCDS o podstawie 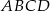ABCD i wierzchołku 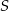trójkąt 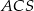ACS jest równoboczny i ma bok długości 8. Oblicz sinus kąta nachylenia ściany bocznej do płaszczyzny podstawy tego ostrosłupa (zobacz rysunek).

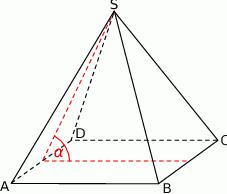
Podstawą ostrosłupa jest romb o boku długości 18 cm. Każda ze ścian bocznych tworzy z płaszczyzną podstawy kąt 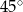45∘ . Pole powierzchni bocznej ostrosłupa jest równe 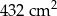43 2 cm 2 . Oblicz jego objętość.

W ostrosłupie prawidłowym czworokątnym przeciwległe krawędzie boczne są prostopadłe, a wysokość ściany bocznej poprowadzona z wierzchołka ostrosłupa ma długość 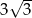√ -- 3 3 . Oblicz objętość i pole powierzchni całkowitej ostrosłupa.

Podstawą ostrosłupa prawidłowego jest kwadrat o przekątnej 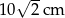√ -- 1 0 2 cm . Krawędź boczna ostrosłupa tworzy z podstawą kąt o mierze 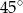45∘ . Oblicz pole powierzchni całkowitej i objętość tego ostrosłupa.

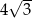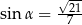W ostrosłupie prawidłowym trójkątnym wysokość ściany bocznej prostopadła do krawędzi podstawy ostrosłupa jest równa √ -- 4 3 i tworzy z krawędzią boczną kąt taki, że √-- -21- sinα = 7 . Oblicz objętość tego ostrosłupa.

Dany jest ostrosłup prawidłowy czworokątny 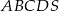ABCDS o podstawie 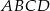ABCD . Pole trójkąta 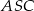ASC jest równe 120, a stosunek długości podstawy tego trójkąta do długości ramienia jest równy 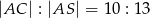|AC | : |AS | = 10 : 13 . Oblicz objętość i pole powierzchni bocznej tego ostrosłupa.

Ostrosłup prawidłowy trójkątny przecięto płaszczyzną, która przechodzi przez krawędź podstawy długości oraz jest prostopadła do przeciwległej krawędzi bocznej. Płaszczyzna ta jest nachylona do płaszczyzny podstawy pod kątem . Oblicz objętość ostrosłupa.

W ostrosłupie prawidłowym czworokątnym pole podstawy jest równe 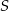, a kąt nachylenia ściany bocznej do płaszczyzny podstawy ma miarę . Ostrosłup przecięto płaszczyzną zawierającą krawędź boczną tego ostrosłupa i przechodzącą przez środek rozłącznej z nią krawędzi podstawy. Oblicz pole otrzymanego przekroju.

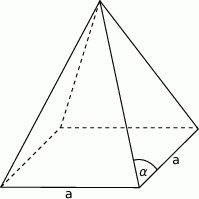
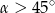W ostrosłupie prawidłowym czworokątnym krawędź podstawy ma długość . Kąt między krawędzią boczną, a krawędzią podstawy ma miarę α > 4 5∘ (zobacz rysunek). Oblicz objętość tego ostrosłupa.

Strona 4 z 11