Wysokość ostrosłupa prawidłowego czworokątnego jest równa 8. Krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem 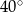 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Prawidłowy czworokątny/Objętość
Wysokość ostrosłupa prawidłowego czworokątnego jest równa 6. Krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem 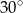 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
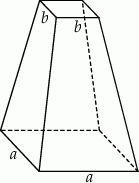
Przedstawiona na rysunku bryła to ostrosłup prawidłowy czworokątny ścięty płaszczyzną równoległą do jego płaszczyzny podstawy. Wysokość tej bryły jest równa 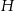 , a
, a  i
i 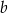 (
(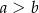 ) są długościami krawędzi jego podstaw. Oblicz objętość tej bryły.
) są długościami krawędzi jego podstaw. Oblicz objętość tej bryły.
W ostrosłupie prawidłowym czworokątnym dane są: 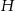 – wysokość ostrosłupa oraz
– wysokość ostrosłupa oraz  — miara kąta utworzonego przez krawędź boczną i krawędź podstawy (
— miara kąta utworzonego przez krawędź boczną i krawędź podstawy (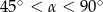 ).
).
- Wykaż, że objętość
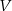 tego ostrosłupa jest równa
tego ostrosłupa jest równa 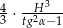 .
. - Oblicz miarę kąta
 , dla której objętość
, dla której objętość 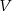 danego ostrosłupa jest równa
danego ostrosłupa jest równa 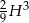 . Wynik podaj w zaookrągleniu do całkowitej liczby stopni.
. Wynik podaj w zaookrągleniu do całkowitej liczby stopni.
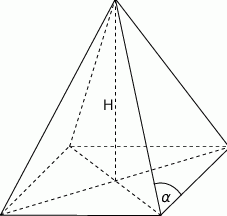
W ostrosłupie prawidłowym czworokątnym ściana boczna o polu równym 10 jest nachylona do płaszczyzny podstawy pod kątem 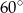 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
W ostrosłupie prawidłowym czworokątnym 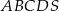 o podstawie
o podstawie 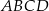 wysokość jest równa 5, a kąt między sąsiednimi ścianami bocznymi ostrosłupa ma miarę
wysokość jest równa 5, a kąt między sąsiednimi ścianami bocznymi ostrosłupa ma miarę 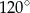 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.

