W ostrosłupie prawidłowym czworokątnym pole podstawy jest równe 100, a pole powierzchni ścian bocznych 320. Oblicz objętość ostrosłupa.
/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Prawidłowy czworokątny/Objętość
Pole podstawy ostrosłupa prawidłowego czworokątnego jest równe 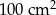 , a jego pole powierzchni bocznej jest równe
, a jego pole powierzchni bocznej jest równe 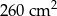 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
W ostrosłupie prawidłowym czworokątnym ściana boczna jest nachylona do płaszczyzny podstawy pod kątem 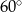 , a krawędź boczna ostrosłupa ma długość
, a krawędź boczna ostrosłupa ma długość 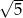 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
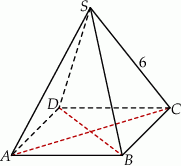
Dany jest ostrosłup prawidłowy czworokątny  , którego krawędź boczna ma długość 6 (zobacz rysunek). Ściana boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem, którego tangens jest równy
, którego krawędź boczna ma długość 6 (zobacz rysunek). Ściana boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem, którego tangens jest równy 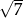 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
W ostrosłupie prawidłowym czworokątnym  krawędź boczna ma długość 6, a kąt nachylenia ściany bocznej do płaszczyzny podstawy ostrosłupa ma miarę
krawędź boczna ma długość 6, a kąt nachylenia ściany bocznej do płaszczyzny podstawy ostrosłupa ma miarę 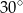 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Oblicz objętość ostrosłupa prawidłowego czworokątnego jeśli jego krawędź boczna o długości 6 nachylona jest do płaszczyzny podstawy pod kątem 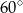 .
.
W ostrosłupie prawidłowym czworokątnym ściana boczna jest nachylona do płaszczyzny podstawy pod kątem ostrym  , dla którego
, dla którego 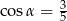 . Wysokość ostrosłupa ma długość 12 cm. Oblicz objętość tego ostrosłupa.
. Wysokość ostrosłupa ma długość 12 cm. Oblicz objętość tego ostrosłupa.
W ostrosłupie prawidłowym czworokątnym ściana boczna jest nachylona do płaszczyzny podstawy pod kątem ostrym  , dla którego
, dla którego 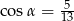 . Wysokość ostrosłupa ma długość 12 cm. Oblicz objętość tego ostrosłupa.
. Wysokość ostrosłupa ma długość 12 cm. Oblicz objętość tego ostrosłupa.
Pole ściany bocznej ostrosłupa prawidłowego czworokątnego jest równe 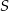 . Kąt płaski przy wierzchołku ostrosłupa ma miarę
. Kąt płaski przy wierzchołku ostrosłupa ma miarę 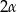 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
W ostrosłupie prawidłowym czworokątnym 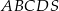 o podstawie
o podstawie 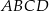 wysokość jest równa
wysokość jest równa 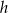 , a kąt między sąsiednimi ścianami bocznymi ostrosłupa ma miarę
, a kąt między sąsiednimi ścianami bocznymi ostrosłupa ma miarę  . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
W ostrosłupie prawidłowym czworokątnym 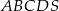 (zobacz rysunek) przekątna
(zobacz rysunek) przekątna 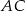 podstawy ma długość
podstawy ma długość 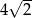 . Kąt
. Kąt 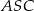 między przeciwległymi krawędziami bocznymi ostrosłupa ma miarę
między przeciwległymi krawędziami bocznymi ostrosłupa ma miarę 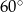 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
W ostrosłupie prawidłowym czworokątnym 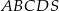 (zobacz rysunek) przekątna
(zobacz rysunek) przekątna 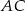 podstawy ma długość 6. Kąt
podstawy ma długość 6. Kąt 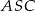 między przeciwległymi krawędziami bocznymi ostrosłupa ma miarę
między przeciwległymi krawędziami bocznymi ostrosłupa ma miarę 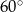 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
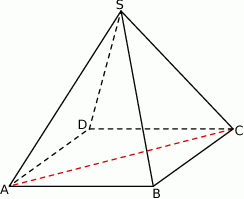
Dany jest ostrosłup prawidłowy czworokątny 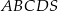 o podstawie
o podstawie 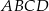 i polu powierzchni bocznej równym
i polu powierzchni bocznej równym  . Kąt między wysokościami sąsiednich ścian bocznych poprowadzonych z wierzchołka
. Kąt między wysokościami sąsiednich ścian bocznych poprowadzonych z wierzchołka 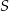 ma miarę
ma miarę 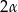 . Objętość tego ostrosłupa jest równa
. Objętość tego ostrosłupa jest równa 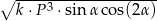 , gdzie
, gdzie 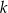 jest stałym współczynnikiem liczbowym. Oblicz współczynnik
jest stałym współczynnikiem liczbowym. Oblicz współczynnik 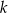 .
.
W ostrosłup prawidłowy czworokątny wpisano kulę o promieniu  . Ściana boczna ostrosłupa nachylona jest do płaszczyzny podstawy pod kątem
. Ściana boczna ostrosłupa nachylona jest do płaszczyzny podstawy pod kątem 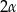 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
W ostrosłup prawidłowy czworokątny wpisano kulę o promieniu 2. Ściana boczna ostrosłupa nachylona jest do płaszczyzny podstawy pod kątem 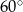 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
W ostrosłupie prawidłowym czworokątnym krawędź podstawy ma długość  . Kąt między krawędzią boczną, a krawędzią podstawy ma miarę
. Kąt między krawędzią boczną, a krawędzią podstawy ma miarę 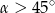 (zobacz rysunek). Oblicz objętość tego ostrosłupa.
(zobacz rysunek). Oblicz objętość tego ostrosłupa.
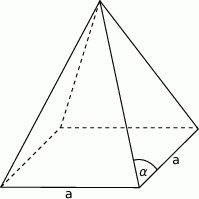
W ostrosłupie prawidłowym czworokątnym krawędź boczna ma długość 4 cm i jest nachylona do płaszczyzny podstawy pod kątem  . Oblicz objętość ostrosłupa.
. Oblicz objętość ostrosłupa.
Wysokość ostrosłupa prawidłowego czworokątnego jest równa 8. Krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem  takim, że
takim, że 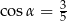 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Oblicz objętość ostrosłupa prawidłowego czworokątnego o krawędzi podstawy 2 dm i krawędzi bocznej 4 dm.
Oblicz objętość ostrosłupa prawidłowego czworokątnego o krawędzi podstawy 4 dm i krawędzi bocznej 6 dm.
Dany jest ostrosłup prawidłowy czworokątny o podstawie 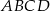 i wierzchołku
i wierzchołku 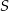 . Pole trójkąta
. Pole trójkąta 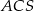 jest równe
jest równe 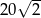 , krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem, którego tangens jest równy
, krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem, którego tangens jest równy 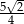 . Oblicz objętość ostrosłupa.
. Oblicz objętość ostrosłupa.
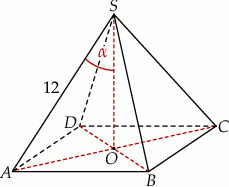
Długość krawędzi bocznej ostrosłupa prawidłowego czworokątnego 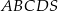 jest równa 12 (zobacz rysunek). Krawędź boczna tworzy z wysokością tego ostrosłupa kąt
jest równa 12 (zobacz rysunek). Krawędź boczna tworzy z wysokością tego ostrosłupa kąt  taki, że
taki, że 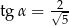 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Długość krawędzi bocznej ostrosłupa prawidłowego czworokątnego 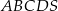 jest równa 12 (zobacz rysunek). Krawędź boczna tworzy z wysokością tego ostrosłupa kąt
jest równa 12 (zobacz rysunek). Krawędź boczna tworzy z wysokością tego ostrosłupa kąt  taki, że
taki, że 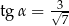 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Krawędź boczna ostrosłupa prawidłowego czworokątnego ma długość 4 cm i jest nachylona do płaszczyzny podstawy pod kątem 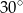 . Oblicz długość krawędzi sześcianu, którego objętość jest równa objętości tego ostrosłupa.
. Oblicz długość krawędzi sześcianu, którego objętość jest równa objętości tego ostrosłupa.
Podstawą ostrosłupa prawidłowego jest kwadrat. Wysokość ściany bocznej tego ostrosłupa jest równa 22, a tangens kąta nachylenia ściany bocznej ostrosłupa do płaszczyzny jego podstawy jest równy 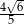 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
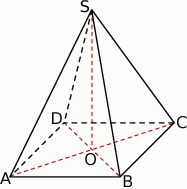
Podstawa ostrosłupa prawidłowego czworokątnego ma pole 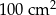 , a jego pole powierzchni bocznej jest równe
, a jego pole powierzchni bocznej jest równe 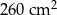 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Wysokość ostrosłupa prawidłowego czworokątnego tworzy ze ścianą boczną kąt o mierze 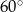 . Pole powierzchni bocznej ostrosłupa jest równe
. Pole powierzchni bocznej ostrosłupa jest równe 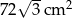 . Oblicz objętość ostrosłupa.
. Oblicz objętość ostrosłupa.
Podstawą ostrosłupa prawidłowego 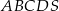 jest kwadrat
jest kwadrat 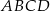 . Punkt
. Punkt 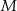 jest środkiem odcinka
jest środkiem odcinka 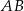 , a punkt
, a punkt 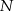 jest środkiem odcinka
jest środkiem odcinka 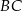 . Trójkąt
. Trójkąt 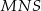 jest równoboczny i jego bok ma długość
jest równoboczny i jego bok ma długość 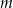 . Oblicz objętość ostrosłupa
. Oblicz objętość ostrosłupa 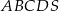 i kąt nachylenia ściany bocznej do płaszczyzny podstawy tego ostrosłupa.
i kąt nachylenia ściany bocznej do płaszczyzny podstawy tego ostrosłupa.

