Na boku 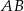 trójkąta
trójkąta 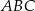 wybrano punkt
wybrano punkt 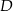 , a na odcinku
, a na odcinku 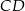 wybrano punkt
wybrano punkt 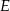 . Wykaż, że stosunek pól trójkątów
. Wykaż, że stosunek pól trójkątów 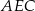 i
i 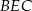 jest równy stosunkowi pól trójkątów
jest równy stosunkowi pól trójkątów 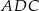 i
i 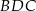 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Na boku 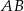 trójkąta
trójkąta 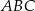 wybrano punkt
wybrano punkt 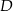 , a na odcinku
, a na odcinku 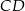 wybrano punkt
wybrano punkt 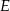 . Wykaż, że stosunek pól trójkątów
. Wykaż, że stosunek pól trójkątów 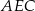 i
i 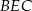 jest równy stosunkowi pól trójkątów
jest równy stosunkowi pól trójkątów 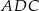 i
i 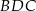 .
.

Środkowa 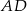 trójkąta
trójkąta 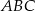 ma długość równą połowie długości boku
ma długość równą połowie długości boku 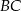 oraz
oraz 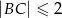 . Wykaż, że
. Wykaż, że 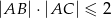 .
.
Dany jest trójkąt rozwartokątny 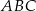 , w którym
, w którym 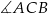 ma miarę
ma miarę 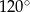 . Ponadto wiadomo, że
. Ponadto wiadomo, że 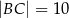 i
i 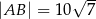 (zobacz rysunek). Oblicz długość trzeciego boku trójkąta
(zobacz rysunek). Oblicz długość trzeciego boku trójkąta 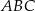 .
.
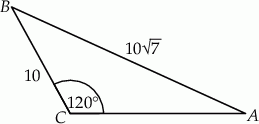
Dany jest trójkąt rozwartokątny 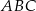 , w którym
, w którym 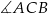 ma miarę
ma miarę 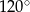 . Ponadto wiadomo, że
. Ponadto wiadomo, że 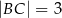 i
i 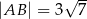 (zobacz rysunek). Oblicz długość trzeciego boku trójkąta
(zobacz rysunek). Oblicz długość trzeciego boku trójkąta 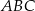 .
.
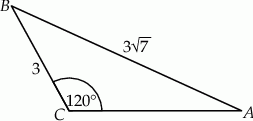
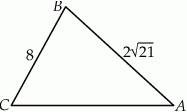
Dany jest trójkąt 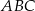 , w którym
, w którym 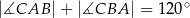 . Ponadto wiadomo, że
. Ponadto wiadomo, że 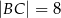 i
i 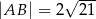 (zobacz rysunek). Oblicz długość trzeciego boku trójkąta
(zobacz rysunek). Oblicz długość trzeciego boku trójkąta 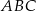 .
.
Kąty ostre trójkąta 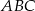 o polu
o polu 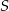 mają miary
mają miary 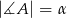 ,
, 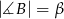 . Oblicz długości boków
. Oblicz długości boków 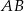 i
i 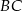 tego trójkąta.
tego trójkąta.
Promień okręgu wpisanego w trójkąt o bokach 5 i 8 jest równy równy 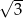 , a obwód tego trójkąta jest liczbą całkowitą. Oblicz długość trzeciego boku tego trójkąta.
, a obwód tego trójkąta jest liczbą całkowitą. Oblicz długość trzeciego boku tego trójkąta.
Punkt 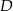 jest środkiem boku
jest środkiem boku 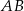 trójkąta
trójkąta 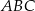 oraz
oraz 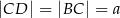 ,
, 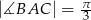 . Oblicz długości boków
. Oblicz długości boków 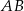 i
i 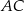 trójkąta
trójkąta 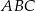 .
.
Na bokach 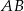 ,
, 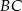 i
i 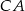 trójkąta
trójkąta 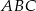 wybrano odpowiednio punkty
wybrano odpowiednio punkty 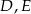 i
i 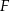 . Wykaż, że okręgi opisane na trójkątach
. Wykaż, że okręgi opisane na trójkątach 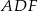 ,
, 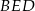 i
i 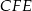 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
W trójkącie 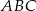 środkowe
środkowe 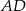 i
i 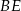 są prostopadłe. Wykaż, że
są prostopadłe. Wykaż, że 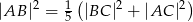 .
.
W trójkącie 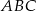 dwa kąty przy wierzchołkach
dwa kąty przy wierzchołkach 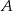 i
i 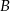 mają odpowiednio miary:
mają odpowiednio miary: 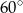 i
i 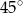 . Oblicz pole tego trójkąta, wiedząc, że długość boku
. Oblicz pole tego trójkąta, wiedząc, że długość boku 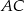 jest równa
jest równa 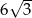 .
.
Wykaż, że jeśli 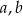 są długościami boków trójkąta ostrokątnego takimi, że
są długościami boków trójkąta ostrokątnego takimi, że 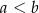 oraz
oraz 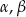 są miarami kątów tego trójkąta leżącymi odpowiednio naprzeciwko boków
są miarami kątów tego trójkąta leżącymi odpowiednio naprzeciwko boków 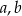 , to
, to 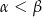 .
.
Dany jest trójkąt 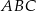 , w którym
, w którym 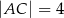 ,
, 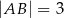 ,
, 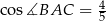 . Oblicz pole trójkąta
. Oblicz pole trójkąta 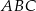 .
.
Dany jest trójkąt 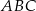 , w którym
, w którym 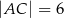 ,
, 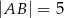 ,
, 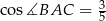 . Oblicz pole trójkąta
. Oblicz pole trójkąta 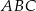 .
.
Dany jest trójkąt 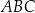 . Na boku
. Na boku 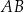 tego trójkąta wybrano punkt
tego trójkąta wybrano punkt 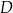 , taki, że
, taki, że 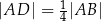 , a na boku
, a na boku 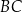 wybrano taki punkt
wybrano taki punkt 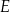 , że
, że 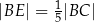 (zobacz rysunek poniżej). Pole trójkąta
(zobacz rysunek poniżej). Pole trójkąta 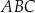 jest równe 20.
jest równe 20.

Oblicz pole trójkąta 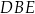 .
.
W trójkącie 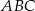 punkt
punkt 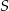 jest środkiem okręgu wpisanego, a punkty
jest środkiem okręgu wpisanego, a punkty 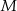 i
i 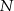 są punktami styczności tego okręgu z bokami
są punktami styczności tego okręgu z bokami 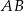 i
i 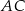 odpowiednio. Wykaż, że punkt
odpowiednio. Wykaż, że punkt 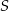 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 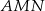 .
.
Stosunek pól dwóch trójkątów podobnych jest równy 4, a suma ich obwodów 12. Wyznacz obwód każdego z tych trójkątów.
Stosunek pól dwóch trójkątów podobnych jest równy 4, a suma ich obwodów 18. Wyznacz obwód każdego z tych trójkątów.
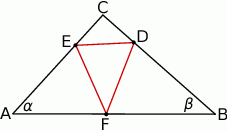
Dany jest trójkąt 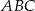 , w którym
, w którym 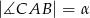 i
i 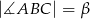 (zobacz rysunek). Na bokach
(zobacz rysunek). Na bokach 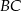 ,
, 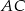 i
i 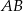 tego trójkąta wybrano odpowiednio punkty
tego trójkąta wybrano odpowiednio punkty 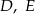 i
i 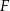 w taki sposób, że
w taki sposób, że 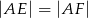 ,
, 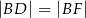 i
i 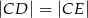 . Oblicz miary kątów trójkąta
. Oblicz miary kątów trójkąta 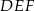 .
.
Wysokość trójkąta 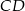 ma długość 4 i dzieli bok
ma długość 4 i dzieli bok 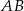 na odcinki, z których krótszy
na odcinki, z których krótszy 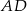 ma długość 2, a kąt
ma długość 2, a kąt 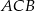 na kąty, których stosunek miar jest równy 1:2. Oblicz długość boku
na kąty, których stosunek miar jest równy 1:2. Oblicz długość boku 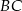 tego trójkąta.
tego trójkąta.
Wykaż, że jeżeli 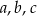 są długościami boków trójkąta leżącymi naprzeciwko odpowiednio kątów o miarach
są długościami boków trójkąta leżącymi naprzeciwko odpowiednio kątów o miarach 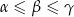 to
to 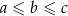 .
.
Dane są dwa boki trójkąta: 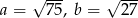 . Jaką długość może przyjmować trzeci bok trójkąta?
. Jaką długość może przyjmować trzeci bok trójkąta?
Każdy kąt trójkąta 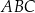 ma miarę mniejszą niż
ma miarę mniejszą niż 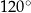 . Udowodnij, że wewnątrz trójkąta
. Udowodnij, że wewnątrz trójkąta 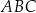 istnieje punkt
istnieje punkt 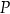 taki, że
taki, że
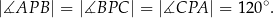
Pole trójkąta ostrokątnego o bokach 40 i 29 jest równe 420. Oblicz długość promienia okręgu wpisanego w ten trójkąt.
