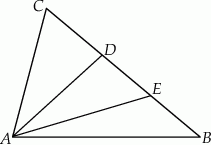
W trójkącie 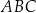 dane są długości boków
dane są długości boków 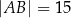 i
i 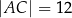 oraz
oraz 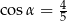 , gdzie
, gdzie 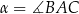 . Na bokach
. Na bokach 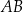 i
i 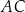 tego trójkąta obrano punkty odpowiednio
tego trójkąta obrano punkty odpowiednio 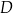 i
i 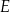 takie, że
takie, że 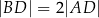 i
i 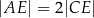 (zobacz rysunek).
(zobacz rysunek).

Oblicz pole
-
trójkąta
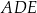 .
. -
czworokąta
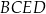 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
W trójkącie 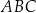 dane są długości boków
dane są długości boków 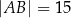 i
i 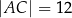 oraz
oraz 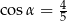 , gdzie
, gdzie 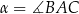 . Na bokach
. Na bokach 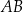 i
i 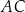 tego trójkąta obrano punkty odpowiednio
tego trójkąta obrano punkty odpowiednio 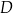 i
i 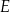 takie, że
takie, że 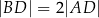 i
i 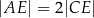 (zobacz rysunek).
(zobacz rysunek).

Oblicz pole
trójkąta 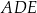 .
.
czworokąta 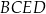 .
.
W trójkącie 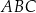 dane są długości boków
dane są długości boków 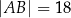 i
i 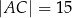 oraz
oraz 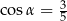 , gdzie
, gdzie 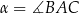 . Na bokach
. Na bokach 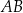 i
i 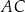 tego trójkąta obrano punkty odpowiednio
tego trójkąta obrano punkty odpowiednio 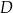 i
i 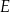 takie, że
takie, że 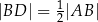 i
i 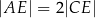 (zobacz rysunek).
(zobacz rysunek).

Oblicz pole
trójkąta 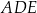 .
.
czworokąta 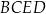 .
.
Liczby 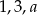 są długościami boków trójkąta. Wyznacz liczbę
są długościami boków trójkąta. Wyznacz liczbę  , wiedząc, że jest to liczba naturalna.
, wiedząc, że jest to liczba naturalna.
Na trójkącie o bokach długości 15, 20, 25 opisano okrąg. Oblicz długość środkowej tego trójkąta poprowadzonej do środka najdłuższego boku.
Odcinek 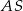 jest środkową trójkąta
jest środkową trójkąta 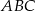 . Udowodnij, że
. Udowodnij, że 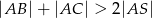 .
.
Okrąg wpisany w trójkąt 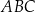 jest styczny do boków
jest styczny do boków 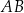 i
i 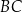 w punktach
w punktach 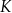 i
i 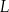 odpowiednio. Na bokach
odpowiednio. Na bokach 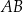 i
i 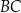 tego trójkąta wybrano punkty
tego trójkąta wybrano punkty 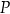 i
i 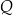 w ten sposób, że odcinek
w ten sposób, że odcinek 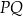 jest styczny do okręgu wpisanego w trójkąt
jest styczny do okręgu wpisanego w trójkąt 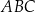 (zobacz rysunek).
(zobacz rysunek).

Wykaż, że jeżeli 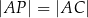 ,
, 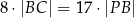 i
i 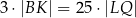 , to trójkąt
, to trójkąt 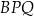 jest rozwartokątny.
jest rozwartokątny.
Ile jest trójkątów o obwodzie równym 19, w których długości boków wyrażone są liczbami całkowitymi. Wymień je.
Punkty 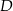 i
i 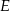 dzielą bok
dzielą bok 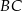 trójkąta
trójkąta 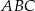 na trzy równe części (zobacz rysunek). Wykaż, że pole trójkąta
na trzy równe części (zobacz rysunek). Wykaż, że pole trójkąta 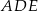 jest trzy razy mniejsze od pola trójkąta
jest trzy razy mniejsze od pola trójkąta 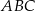 .
.
W trójkącie 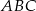 dane są:
dane są: 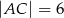 ,
, 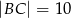 i kąt
i kąt 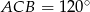 . Wyznacz długość środkowej
. Wyznacz długość środkowej 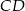 tego trójkąta.
tego trójkąta.
Wykaż, że suma odległości dowolnego punktu wewnętrznego trójkąta od jego wierzchołków jest większa od połowy obwodu trójkąta.
Na rysunku przedstawiono trójkąt 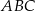 , w którym
, w którym 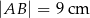 oraz odcinek
oraz odcinek 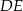 równoległy do boku
równoległy do boku 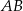 trójkąta.
trójkąta.
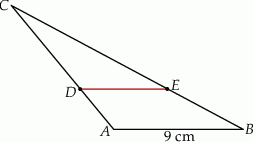
Stosunek pola trapezu 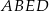 do pola trójkąta
do pola trójkąta 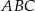 jest równy
jest równy 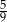 . Oblicz długość odcinka
. Oblicz długość odcinka 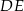 .
.
Wysokość 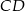 trójkąta
trójkąta 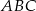 ma długość 6cm i dzieli bok
ma długość 6cm i dzieli bok 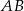 na odcinki o długościach
na odcinki o długościach 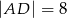 i
i 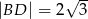 .
.
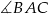 .
. 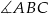 .
.Wykaż, że odcinek łączący środki dwóch boków trójkąta jest równoległy do trzeciego boku i ma długość równą połowie tego boku.
Dwusieczne kątów 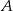 i
i 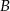 trójkąta
trójkąta 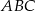 przecinają okrąg opisany na nim odpowiednio w punktach
przecinają okrąg opisany na nim odpowiednio w punktach 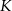 i
i 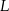 . Oblicz miary kątów czworokąta
. Oblicz miary kątów czworokąta 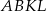 wiedząc, że
wiedząc, że 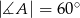 i
i 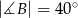 .
.
W trójkącie ostrokątnym 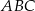 prawdziwa jest równość
prawdziwa jest równość 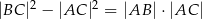 . Wykaż, że kąt
. Wykaż, że kąt 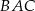 jest dwa razy większy od kąta
jest dwa razy większy od kąta 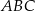 .
.
Wykaż, że jeżeli w trójkącie dwusieczna pokrywa się ze środkową, to trójkąt ten jest równoramienny.
Wyraź pole trójkąta w zależności od długości jednego z jego boków i miar kątów doń przyległych.
W trójkącie 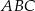 punkt
punkt 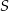 jest środkiem okręgu wpisanego, a punkty
jest środkiem okręgu wpisanego, a punkty 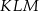 są punktami styczności okręgu wpisanego w trójkąt z bokami
są punktami styczności okręgu wpisanego w trójkąt z bokami 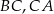 i
i 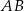 odpowiednio.
odpowiednio.
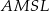 można opisać okrąg.
można opisać okrąg. 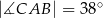 oraz
oraz 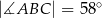 oblicz miary kątów trójkąta
oblicz miary kątów trójkąta 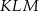 .
.Wykaż, że jeżeli 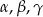 są kątami trójkąta, to
są kątami trójkąta, to
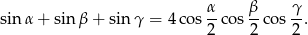
Punkty 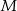 i
i 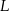 leżą odpowiednio na bokach
leżą odpowiednio na bokach 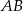 i
i 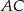 trójkąta
trójkąta 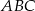 , przy czym zachodzą równości
, przy czym zachodzą równości 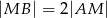 oraz
oraz 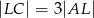 . Punkt
. Punkt 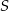 jest punktem przecięcia odcinków
jest punktem przecięcia odcinków 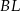 i
i 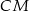 . Punkt
. Punkt 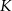 jest punktem przecięcia półprostej
jest punktem przecięcia półprostej 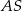 z odcinkiem
z odcinkiem 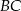 (zobacz rysunek).
(zobacz rysunek).
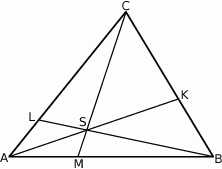
Pole trójkąta 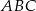 jest równe 660. Oblicz pola trójkątów:
jest równe 660. Oblicz pola trójkątów: 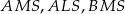 i
i 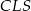 .
.
Punkty 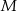 i
i 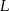 leżą odpowiednio na bokach
leżą odpowiednio na bokach 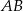 i
i 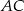 trójkąta
trójkąta 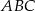 , przy czym zachodzą równości
, przy czym zachodzą równości 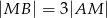 oraz
oraz 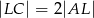 . Punkt
. Punkt 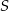 jest punktem przecięcia odcinków
jest punktem przecięcia odcinków 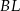 i
i 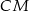 . Punkt
. Punkt 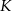 jest punktem przecięcia półprostej
jest punktem przecięcia półprostej 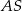 z odcinkiem
z odcinkiem 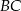 (zobacz rysunek).
(zobacz rysunek).
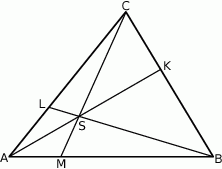
Pole trójkąta 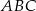 jest równe 528. Oblicz pola trójkątów:
jest równe 528. Oblicz pola trójkątów: 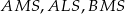 i
i 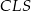 .
.
W trójkącie 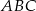 środkowa
środkowa 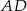 jest prostopadła do boku
jest prostopadła do boku 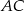 . Kąt
. Kąt 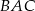 ma miarę
ma miarę 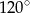 . Wykaż, że
. Wykaż, że 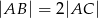 .
.
