Wykaż, że jeżeli 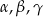 są kątami wewnętrznymi trójkąta i
są kątami wewnętrznymi trójkąta i 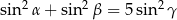 , to
, to 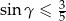 .
.
/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny
W trójkącie 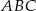 poprowadzono dwusieczne kątów
poprowadzono dwusieczne kątów 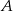 i
i 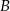 . Dwusieczne te przecinają się w punkcie
. Dwusieczne te przecinają się w punkcie 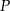 . Uzasadnij, że kąt
. Uzasadnij, że kąt 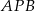 jest rozwarty.
jest rozwarty.
W trójkącie ostrokątnym 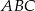 proste
proste 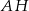 i
i 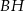 zawierają wysokości poprowadzone z wierzchołków
zawierają wysokości poprowadzone z wierzchołków 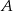 i
i 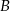 . Uzasadnij, że kąt
. Uzasadnij, że kąt 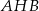 jest rozwarty.
jest rozwarty.
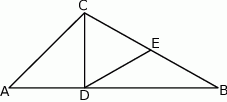
Dany jest trójkąt 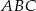 . Odcinek
. Odcinek 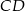 jest wysokością tego trójkąta, punkt
jest wysokością tego trójkąta, punkt 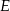 jest środkiem boku
jest środkiem boku 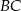 (tak jak na rysunku) i
(tak jak na rysunku) i 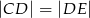 . Udowodnij, że trójkąt
. Udowodnij, że trójkąt 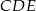 jest równoboczny.
jest równoboczny.
Wykaż, że jeżeli kąty trójkąta: 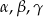 spełniają równanie
spełniają równanie 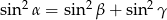 to trójkąt jest prostokątny.
to trójkąt jest prostokątny.
W trójkącie ostrokątnym 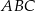 bok
bok 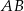 ma długość 18 cm, a wysokość
ma długość 18 cm, a wysokość 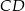 jest równa 15 cm. Punkt
jest równa 15 cm. Punkt 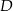 dzieli bok
dzieli bok 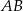 tak, że
tak, że 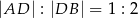 . Przez punkt
. Przez punkt 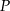 leżący na odcinku
leżący na odcinku 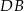 poprowadzono prostą równoległą do prostej
poprowadzono prostą równoległą do prostej 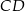 , odcinając od trójkąta
, odcinając od trójkąta 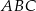 trójkąt, którego pole jest cztery razy mniejsze niż pole trójkąta
trójkąt, którego pole jest cztery razy mniejsze niż pole trójkąta 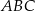 . Oblicz długość odcinka
. Oblicz długość odcinka 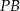 .
.
Wykaż, że jeżeli środkowa trójkąta jest dwa razy krótsza od boku, do którego jest poprowadzona, to trójkąt ten jest prostokątny.
Punkt 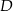 leży na boku
leży na boku 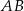 trójkąta
trójkąta 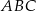 oraz
oraz 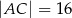 ,
, 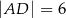 ,
, 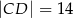 i
i 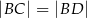 . Oblicz obwód trójkąta
. Oblicz obwód trójkąta 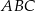 .
.
W trójkącie 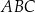 , w którym
, w którym 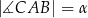 , poprowadzono dwusieczną
, poprowadzono dwusieczną 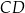 kąta wewnętrznego
kąta wewnętrznego 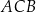 , przy czym
, przy czym 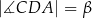 . Oblicz
. Oblicz 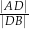 .
.
Dany jest trójkąt o bokach długości 7,8,9.
- Oblicz promień okręgu wpisanego w ten trójkąt.
- Oblicz sumę sinusów kątów tego trójkąta.
Dane są miary łukowe dwóch kątów trójkąta: 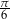 i
i 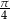 . Wyznacz miarę trzeciego kąta w stopniach i radianach.
. Wyznacz miarę trzeciego kąta w stopniach i radianach.
Dane są miary łukowe dwóch kątów trójkąta: 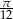 i
i 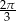 . Wyznacz miarę trzeciego kąta w stopniach i radianach.
. Wyznacz miarę trzeciego kąta w stopniach i radianach.
Dane są miary łukowe dwóch kątów trójkąta: 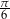 i
i 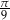 . Wyznacz miarę trzeciego kąta w stopniach i radianach.
. Wyznacz miarę trzeciego kąta w stopniach i radianach.
Dane są miary łukowe dwóch kątów trójkąta: 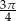 i
i 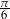 . Wyznacz miarę trzeciego kąta w stopniach i radianach.
. Wyznacz miarę trzeciego kąta w stopniach i radianach.
W trójkącie 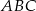 dane są:
dane są: 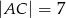 ,
, 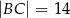 i
i 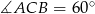 . Oblicz pole trójkąta
. Oblicz pole trójkąta 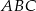 .
.
- Uzasadnij, że jeśli długości boków trójkąta są równe
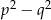 ,
, 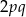 i
i 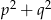 , gdzie
, gdzie 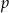 i
i 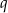 są liczbami dodatnimi takimi, że
są liczbami dodatnimi takimi, że 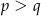 , to trójkąt ten jest prostokątny.
, to trójkąt ten jest prostokątny. - Wyznacz wszystkie naturalne wartości
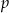 i
i 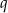 , dla których najkrótszy bok otrzymanego trójkąta ma długość 13.
, dla których najkrótszy bok otrzymanego trójkąta ma długość 13.
Udowodnij, że jeżeli środek okręgu opisanego na trójkącie leży na jednym z jego boków, to trójkąt ten jest prostokątny.
Oblicz sumę długości środkowych trójkąta o długościach boków: 2, 3 i 4.
Wykaż, że jeżeli długości 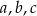 boków trójkąta spełniają równość
boków trójkąta spełniają równość
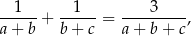
to promień okręgu opisanego na tym trójkącie jest równy 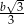 .
.
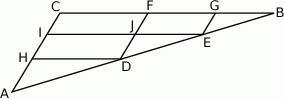
Odcinki 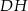 i
i 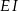 są równoległe do boku
są równoległe do boku 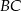 trójkąta
trójkąta 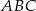 , a odcinki
, a odcinki 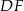 i
i 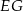 są równoległe do boku
są równoległe do boku 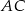 . Uzasadnij, że jeżeli
. Uzasadnij, że jeżeli 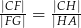 , to
, to 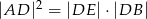 .
.
W trójkącie 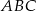 dane są
dane są 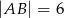 ,
, 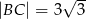 oraz
oraz 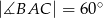 . Oblicz pole trójkąta
. Oblicz pole trójkąta 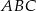 .
.
W trójkącie 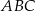 poprowadzono dwusieczne kątów przecinające boki
poprowadzono dwusieczne kątów przecinające boki 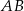 i
i 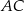 tego trójkąta w punktach – odpowiednio –
tego trójkąta w punktach – odpowiednio – 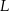 i
i 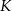 . Punkt
. Punkt 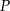 jest punktem przecięcia tych dwusiecznych. Długości boków trójkąta
jest punktem przecięcia tych dwusiecznych. Długości boków trójkąta 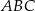 spełniają warunki:
spełniają warunki: 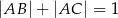 oraz
oraz
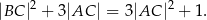
Udowodnij, że punkt 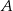 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 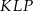 .
.
W trójkącie 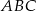 dwusieczna kąta
dwusieczna kąta 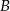 przecina bok
przecina bok 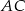 w punkcie
w punkcie 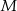 . Przez punkt
. Przez punkt 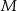 prowadzimy prostą równoległą do
prowadzimy prostą równoległą do 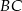 , przecinającą bok
, przecinającą bok 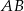 w punkcie
w punkcie 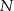 (rys.). Udowodnij, że
(rys.). Udowodnij, że 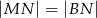 .
.
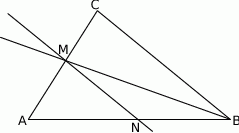
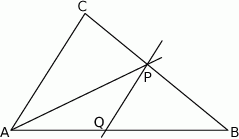
W trójkącie 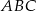 dwusieczna kąta
dwusieczna kąta 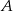 przecina bok
przecina bok 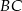 w punkcie
w punkcie 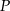 . Przez punkt
. Przez punkt 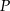 prowadzimy prostą równoległą do
prowadzimy prostą równoległą do 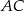 , przecinającą bok
, przecinającą bok 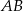 w punkcie
w punkcie 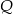 (rys.). Udowodnij, że
(rys.). Udowodnij, że 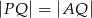 .
.
Wykaż, że jeżeli kąty 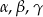 trójkąta
trójkąta 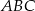 spełniają warunek
spełniają warunek 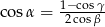 to trójkąt jest równoramienny.
to trójkąt jest równoramienny.

