W trójkącie 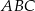 środkowa
środkowa 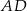 jest prostopadła do boku
jest prostopadła do boku 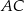 . Kąt
. Kąt 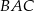 ma miarę
ma miarę 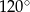 oraz
oraz 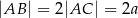 . Oblicz długość odcinka
. Oblicz długość odcinka 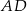 .
.
/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny
Dwa boki trójkąta ostrokątnego wpisanego w okrąg o promieniu 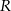 mają długości
mają długości 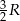 i
i 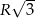 . Wykaż, że długość trzeciego boku wynosi
. Wykaż, że długość trzeciego boku wynosi 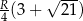 .
.
Trzy cięciwy okręgu o promieniu  tworzą trójkąt wpisany w ten okrąg. Dwie najkrótsze z tych cięciw mają długości
tworzą trójkąt wpisany w ten okrąg. Dwie najkrótsze z tych cięciw mają długości 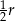 i
i 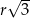 . Wykaż, że trzecia cięciwa ma długość
. Wykaż, że trzecia cięciwa ma długość 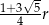 .
.
Wykaż, że jeżeli 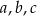 są długościami boków trójkąta to
są długościami boków trójkąta to 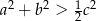 .
.
Na bokach trójkąta zbudowano kwadraty o polach 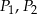 i
i  (zobacz rysunek)
(zobacz rysunek)
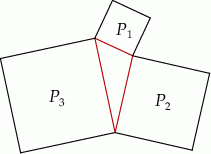
Wykaż, że 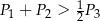 .
.
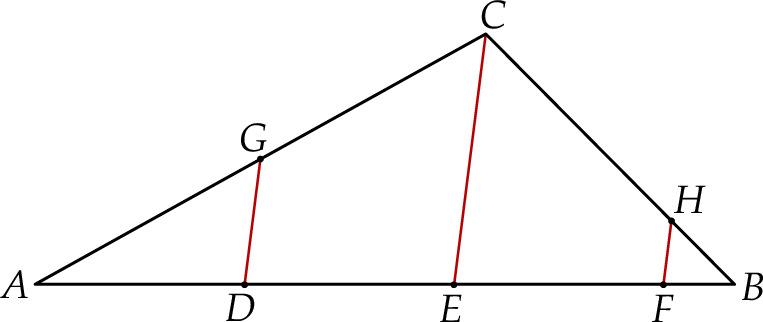
Trójkąt podzielono odcinkami 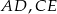 i
i 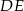 na 5 trójkątów, przy czym
na 5 trójkątów, przy czym 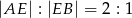 .
.
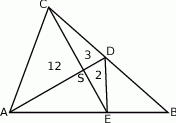
Korzystając z podanych pól trzech z tych trójkątów, wyznacz pole trójkąta 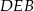 .
.
Długości dwóch boków trójkąta są równe 1 i 4, a miara kąta zawartego między nimi wynosi 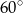 .
.
- Oblicz pole tego trójkąta.
- Oblicz promień okręgu opisanego na tym trójkącie.
- Oblicz promień okręgu wpisanego w ten trójkąt.
Styczna w punkcie 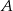 do okręgu opisanego na trójkącie
do okręgu opisanego na trójkącie 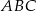 przecina prostą
przecina prostą 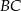 w punkcie
w punkcie 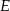 . Niech
. Niech 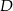 będzie punktem przecięcia dwusiecznej kąta
będzie punktem przecięcia dwusiecznej kąta 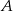 z prostą
z prostą 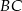 . Udowodnić, że
. Udowodnić, że 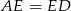 .
.
W trójkącie 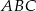 , o bokach długości
, o bokach długości 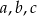 , połączono odcinkiem wierzchołek
, połączono odcinkiem wierzchołek 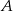 z punktem
z punktem 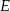 na boku
na boku 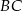 takim, że
takim, że 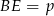 i
i 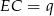 . Uzasadnij, że jeżeli
. Uzasadnij, że jeżeli 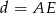 , to
, to 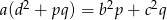 (twierdzenie Stewarta).
(twierdzenie Stewarta).
W okrąg wpisano trójkąt 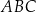 , w którym
, w którym 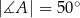 i
i 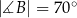 . Przez wierzchołek kąta
. Przez wierzchołek kąta 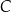 poprowadzono styczną do okręgu, przecinającą przedłużenie boku
poprowadzono styczną do okręgu, przecinającą przedłużenie boku 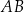 w punkcie
w punkcie 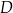 . Oblicz miary kątów trójkąta
. Oblicz miary kątów trójkąta 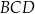 .
.
W trójkącie 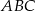 wysokość
wysokość 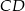 dzieli bok
dzieli bok 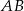 na odcinki długości
na odcinki długości 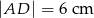 i
i 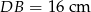 . Bok
. Bok 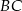 ma 20 cm długości. Poprowadzono symetralną boku
ma 20 cm długości. Poprowadzono symetralną boku 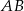 . Wyznacz długości odcinków, na jakie symetralna ta podzieliła bok
. Wyznacz długości odcinków, na jakie symetralna ta podzieliła bok 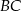 .
.
W trójkącie 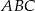 wysokość
wysokość 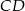 dzieli bok
dzieli bok 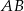 na odcinki długości
na odcinki długości 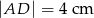 i
i 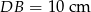 . Bok
. Bok 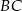 ma 16 cm długości. Poprowadzono symetralną boku
ma 16 cm długości. Poprowadzono symetralną boku 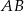 . Wyznacz długości odcinków, na jakie symetralna ta podzieliła bok
. Wyznacz długości odcinków, na jakie symetralna ta podzieliła bok 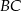 .
.
W trójkącie 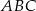 bok
bok 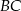 ma długość 24 cm. Oblicz obwód tego trójkąta, wiedząc, że miara kąta przy wierzchołku
ma długość 24 cm. Oblicz obwód tego trójkąta, wiedząc, że miara kąta przy wierzchołku 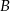 jest równa
jest równa 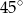 , a miara kąta przy wierzchołku
, a miara kąta przy wierzchołku 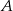 jest równa
jest równa 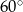 .
.
W trójkącie 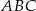 bok
bok 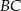 ma długość 12 cm. Oblicz obwód tego trójkąta, wiedząc, że miara kąta przy wierzchołku
ma długość 12 cm. Oblicz obwód tego trójkąta, wiedząc, że miara kąta przy wierzchołku 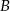 jest równa
jest równa 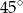 , a miara kąta przy wierzchołku
, a miara kąta przy wierzchołku 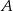 jest równa
jest równa 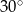 .
.
Wysokość 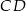 trójkąta
trójkąta 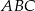 tworzy z bokami
tworzy z bokami 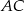 i
i 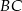 kąty o miarach równych odpowiednio
kąty o miarach równych odpowiednio 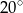 i
i 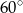 . Punkt
. Punkt 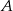 należy do odcinka
należy do odcinka 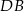 .
.
- Narysuj trójkąt
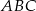 i jego wysokość
i jego wysokość 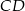 .
. - Wyznacz miary kątów trójkąta
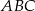 .
.
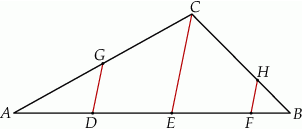
Dany jest trójkąt 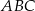 . Na boku
. Na boku 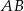 tego trójkąta obrano punkty
tego trójkąta obrano punkty 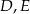 i
i 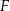 tak, że
tak, że 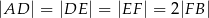 . Na bokach
. Na bokach 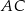 i
i 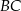 obrano – odpowiednio – punkty
obrano – odpowiednio – punkty 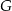 i
i 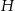 tak, że
tak, że 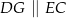 oraz
oraz 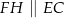 (zobacz rysunek). Wykaż, że jeżeli pole trójkąta
(zobacz rysunek). Wykaż, że jeżeli pole trójkąta 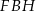 jest równe
jest równe 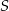 , to pole trójkąta
, to pole trójkąta 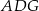 jest równe
jest równe 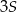 .
.
Dany jest trójkąt  . Na boku
. Na boku  tego trójkąta obrano punkty
tego trójkąta obrano punkty  i
i 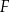 tak, że
tak, że 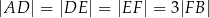 . Na bokach
. Na bokach 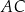 i
i 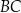 obrano – odpowiednio – punkty
obrano – odpowiednio – punkty 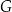 i
i 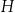 tak, że
tak, że 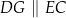 oraz
oraz 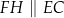 (zobacz rysunek). Wykaż, że jeżeli pole trójkąta
(zobacz rysunek). Wykaż, że jeżeli pole trójkąta 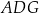 jest równe
jest równe 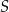 , to pole trójkąta
, to pole trójkąta 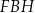 jest równe
jest równe 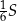 .
.
Wykaż, że jeśli  i
i 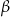 są kątami trójkąta oraz
są kątami trójkąta oraz 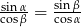 to trójkąt ten jest równoramienny lub prostokątny.
to trójkąt ten jest równoramienny lub prostokątny.
Kąty w trójkącie mają miary: 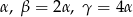 . Wykaż, że długości boków
. Wykaż, że długości boków 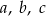 tego trójkąta spełniają równość:
tego trójkąta spełniają równość: 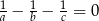 .
.
W trójkącie ostrokątnym 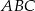 , którego pole równa się 16, boki
, którego pole równa się 16, boki 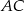 i
i 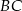 mają długości
mają długości 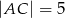 ,
, 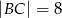 . Oblicz długość boku
. Oblicz długość boku 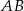 .
.
Punkty 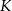 i
i 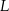 są środkami boków
są środkami boków 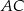 i
i 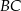 trójkąta
trójkąta 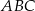 . Odcinki
. Odcinki 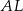 i
i 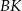 przecinają się w punkcie
przecinają się w punkcie 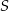 .
.
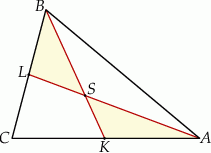
Uzasadnij, że pola trójkątów 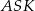 i
i 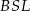 są równe.
są równe.
Punkt 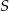 jest punktem przecięcia się wysokości trójkąta ostrokątnego
jest punktem przecięcia się wysokości trójkąta ostrokątnego 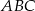 . Wykaż, że jeżeli
. Wykaż, że jeżeli 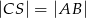 to
to 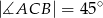 .
.
Środkowa trójkąta jest równa połowie boku, do którego została poprowadzona. Wykaż, że trójkąt ten jest prostokątny.
W trójkącie ostrokątnym 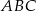 dane są
dane są 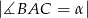 i
i 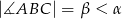 . Wykaż, że tangens kąta utworzonego przez środkową i wysokość opuszczone z wierzchołka
. Wykaż, że tangens kąta utworzonego przez środkową i wysokość opuszczone z wierzchołka 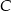 jest równy
jest równy
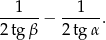
Dany jest trójkąt o bokach długości 4 (podstawa trójkąta), 5 i 6 – boki trójkąta. Przez punkt przecięcia się środkowych trójkąta prowadzimy prostą równoległą do podstawy. Oblicz obwód trójkąta którego podstawą jest ta prosta.

