Prosta 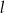 , na której leży punkt
, na której leży punkt 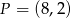 , tworzy z dodatnimi półosiami układu współrzędnych trójkąt prostokątny o polu równym 36. Wyznacz równanie prostej
, tworzy z dodatnimi półosiami układu współrzędnych trójkąt prostokątny o polu równym 36. Wyznacz równanie prostej 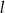 .
.
/Szkoła średnia/Geometria/Geometria analityczna/Równanie prostej/Różne
Prosta 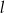 , na której leży punkt
, na której leży punkt 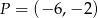 , tworzy z ujemnymi półosiami układu współrzędnych trójkąt prostokątny o polu równym 24. Wyznacz równanie prostej
, tworzy z ujemnymi półosiami układu współrzędnych trójkąt prostokątny o polu równym 24. Wyznacz równanie prostej 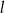 .
.
Dane są punkty 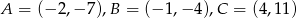 . Wykaż, że punkty te są współliniowe
. Wykaż, że punkty te są współliniowe
Wyznacz równanie prostej, która przecina oś 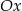 pod kątem
pod kątem 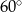 , a oś
, a oś 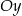 w punkcie
w punkcie 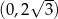 .
.
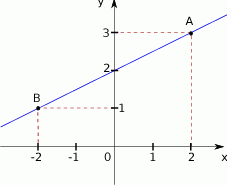
Na płaszczyźnie dane są punkty 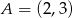 i
i 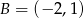 (patrz rysunek). Zbadaj, czy punkty
(patrz rysunek). Zbadaj, czy punkty 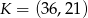 i
i 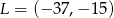 leżą po tej samej stronie prostej
leżą po tej samej stronie prostej 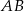 . Podaj odpowiedź i jej uzasadnienie.
. Podaj odpowiedź i jej uzasadnienie.
Początkowe ramię kąta  pokrywa się z dodatnią półosią osi odciętych, a na końcowym ramieniu tego kąta leży punkt
pokrywa się z dodatnią półosią osi odciętych, a na końcowym ramieniu tego kąta leży punkt 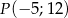 . Oblicz wartość wyrażenia:
. Oblicz wartość wyrażenia: 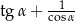 .
.
Początkowe ramię kąta  pokrywa się z dodatnią półosią osi odciętych, a na końcowym ramieniu tego kąta leży punkt
pokrywa się z dodatnią półosią osi odciętych, a na końcowym ramieniu tego kąta leży punkt 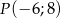 . Oblicz wartość wyrażenia:
. Oblicz wartość wyrażenia: 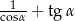 .
.
Jaką figurę na płaszczyźnie określa podane równanie parametryczne:
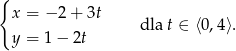
Jaką figurę na płaszczyźnie określa podane równanie parametryczne:
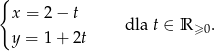
Dany jest ciąg 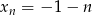 dla
dla 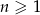 . Ciąg
. Ciąg 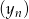 ma tę własność, że dla każdego
ma tę własność, że dla każdego 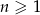 punkty o współrzędnych
punkty o współrzędnych 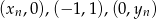 leżą na jednej prostej. Wyznacz wzór ogólny ciągu
leżą na jednej prostej. Wyznacz wzór ogólny ciągu 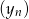 .
.
Dany jest punkt 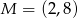 . Wyznacz równanie takiej prostej
. Wyznacz równanie takiej prostej 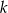 , do której należy punkt
, do której należy punkt 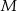 , że na ujemnej półosi
, że na ujemnej półosi 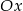 i dodatniej półosi
i dodatniej półosi 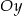 układu
układu 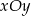 prosta ta wyznacza odcinki
prosta ta wyznacza odcinki 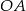 i
i 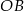 , których suma długości jest równa 6. Oblicz obwód trójkąta
, których suma długości jest równa 6. Oblicz obwód trójkąta 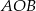 .
.

