Pewna choroba dotyka 0,2% całej populacji i w początkowym stadium nie daje widocznych objawów chorobowych. W ramach profilaktyki stosuje się pewien test przesiewowy, który daje wynik pozytywny lub negatywny. Prawdopodobieństwo tego, że test wykonany na osobie chorej da wynik pozytywny (oznaczający chorobę), jest równe 0,99. Ponadto wiadomo, że prawdopodobieństwo tego, że test wykonany na osobie zdrowej da wynik negatywny, jest równe 0,98. Pan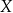 
poddał się testowi, który dał wynik pozytywny. Pozytywny wynik oznacza podejrzenie choroby. Oblicz prawdopodobieństwo tego, że pan 
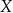jest rzeczywiście chory. Wynik zapisz w postaci ułamka dziesiętnego w zaokrągleniu do części setnych.
/Szkoła średnia/Prawdopodobieństwo/Warunkowe i całkowite/Liczba osób
Wśród 200 uczniów pewnego krakowskiego gimnazjum przeprowadzono ankietę dotyczącą planów wakacyjnych. Wyniki ankiety przedstawiono w tabeli.
| Klasa | Liczba uczniów | Liczba uczniów, którzy nie wyjadą na wakacje | Liczba uczniów, którzy wyjadą z rodzicami | Liczba uczniów, którzy wyjadą na kolonie |
| Pierwsza | 50 | 8 | 36 | 12 |
| Druga | 80 | 16 | 48 | 24 |
| Trzecia | 70 | 12 | 40 | 24 |
Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że losowo wybrana osoba, spośród ankietowanych, wyjedzie na wakacje, jeśli wiadomo, że ta osoba nie jest uczniem drugiej klasy.
Wśród uczniów pewnej szkoły przeprowadzono ankietę dotyczącą posiadanego rodzeństwa i okazało się, że:
– prawdopodobieństwo, że losowo wybrany uczeń ma brata jest równe 0,6;
– jeżeli wybierzemy losowo ucznia, który ma brata, to prawdopodobieństwo, że ten uczeń ma również siostrę jest równe 0,3;
– jeżeli wybierzemy losowo ucznia, który ma brata i ma siostrę, to prawdopodobieństwo, że ten uczeń jest uczniem klasy pierwszej jest równe 0,4.
Oblicz jakie jest prawdopodobieństwo, że losowo wybrany uczeń tej szkoły jest uczniem klasy pierwszej, który ma brata i siostrę.
W klasach 3a, 3b i 3c przeprowadzono sprawdzian. Losowo wybieramy klasę, a następnie ucznia z tej klasy. Jakie jest prawdopodobieństwo, że wybrany uczeń otrzymał ocenę co najmniej 4, jeżeli wiadomo, że
w klasie 3a: wszystkich uczniów jest 20, uczniów z oceną co najmiej cztery jest 8;
w klasie 3b: wszystkich uczniów jest 21, uczniów z oceną co najmiej cztery jest 14;
w klasie 3c: wszystkich uczniów jest 18, uczniów z oceną co najmiej cztery jest 6.
Wśród 390 pracowników pewnej firmy jest 150 kobiet i 240 mężczyzn. Wśród nich w wieku przedemerytalnym jest 21 kobiet i 43 mężczyzn. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że losowo wybrany pracownik tej firmy jest w wieku przedemerytalnym – pod warunkiem że jest mężczyzną.
W klasie IIIA jest 12 dziewcząt i 14 chłopców, natomiast w klasie IIIB jest 10 dziewcząt i 16 chłopców. Rzucamy cztery razy sześcienną kostką do gry. Jeśli suma wyrzuconych oczek jest liczbą parzystą i co najmniej na jednej kostce wypadła parzysta liczba oczek, to wybieramy trzyosobową delegację z klasy IIIA, w przeciwnym wypadku z klasy IIIB. Oblicz prawdopodobieństwo, że w skład delegacji wejdzie co najmniej jeden chłopiec.
Wśród 10 tysięcy mieszkańców pewnego miasta przeprowadzono sondaż dotyczący budowy przedszkola publicznego. Wyniki sondażu przedstawiono w tabeli.
| Badane grupy | Liczba osób popierających budowę przedszkola | Liczba osób niepopierających budowy przedszkola |
| Kobiety | 5140 | 1860 |
| Mężczyźni | 2260 | 740 |
Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że losowo wybrana osoba, spośród ankietowanych, popiera budowę przedszkola, jeśli wiadomo, że jest mężczyzną.
Ukryj
Podobne zadania
Wśród 1200 uczniów pewnego liceum przeprowadzono sondaż dotyczący funkcjonowania sklepiku szkolnego. Wyniki sondażu przedstawiono w tabeli.
| Badane grupy | Liczba uczniów zadowolonych z asortymentu sklepiku | Liczba uczniów niezadowolonych z asortymentu sklepiku |
| Chłopcy | 320 | 260 |
| Dziewczęta | 280 | 340 |
Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że losowo wybrana osoba, spośród ankietowanych, jest zadowolona z asortymentu sklepiku, jeśli wiadomo, że jest dziewczynką.
Urzędnik bankowy wie, że 12% kredytobiorców hipotecznych traci pracę i przestaje spłacać pożyczkę w ciągu 5 lat. Wie też, że 20% kredytobiorców hipotecznych traci pracę w ciągu 5 lat. Przy założeniu, że kredytobiorca hipoteczny stracił pracę, jakie jest prawdopodobieństwo, iż przestanie spłacać pożyczkę.
Na stu mężczyzn ośmiu, zaś na tysiąc kobiet pięć ma zaburzenie rozpoznawania barw. Z grupy, w której stosunek liczby mężczyzn do liczby kobiet wynosi 7:11 wybrano losowo jedną osobę. Jakie jest prawdopodobieństwo, że wylosowana osoba prawidłowo rozpoznaje kolory?
W firmie zatrudniającej 390 pracowników sporządzono zestawienie wszystkich pracowników w wieku przedemerytalnym i okazało się, że wśród nich jest 96 mężczyzn i 45 kobiet. Prawdopodobieństwo zdarzenia polegającego na tym, że losowo wybrany mężczyzna pracujący w tej firmie jest w wieku przedemerytalnym jest równe 0,4. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że losowo wybrany pracownik tej firmy jest w wieku przedemerytalnym – pod warunkiem, że jest to kobieta.
