Przy produkcji pewnego wyrobu wykonuje się dwie kolejno następujące po sobie operacje: cięcie i szlifowanie. Prawdopodobieństwa uszkodzenia obrabianego elementu w każdej z tych operacji wynoszą odpowiednio 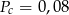 i
i 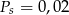 .
.
- Oblicz prawdopodobieństwo, że podany obróbce element zostanie uszkodzony.
- Ile powinno wynosić prawdopodobieństwo
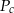 by prawdopodobieństwo uszkodzenia elementu w trakcie obróbki wynosiło mniej niż 0,069?
by prawdopodobieństwo uszkodzenia elementu w trakcie obróbki wynosiło mniej niż 0,069?

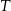 ) elementów z fabryki I jest równa 0,9, a z fabryki II 0,7. W sposób przypadkowy wzięto jeden element z magazynu i okazało się, że był sprawny przez czas
) elementów z fabryki I jest równa 0,9, a z fabryki II 0,7. W sposób przypadkowy wzięto jeden element z magazynu i okazało się, że był sprawny przez czas 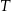 . Obliczyć prawdopodobieństwo, że wybrany element pochodzi z fabryki I.
. Obliczyć prawdopodobieństwo, że wybrany element pochodzi z fabryki I. 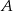 , 40 sztuk z powodu wady
, 40 sztuk z powodu wady 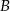 , pozostałe z powodu wady
, pozostałe z powodu wady 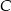 . Każda część ma tylko jedną wadę. Oblicz prawdopodobieństwo, że wybierając losowo z tego pojemnika 3 części, wybierzesz dokładnie po jednej części z każdą z wad.
. Każda część ma tylko jedną wadę. Oblicz prawdopodobieństwo, że wybierając losowo z tego pojemnika 3 części, wybierzesz dokładnie po jednej części z każdą z wad. 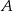 , 40 sztuk z powodu wady
, 40 sztuk z powodu wady 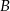 , pozostałe z powodu wady
, pozostałe z powodu wady 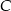 . Każda część ma tylko jedną wadę. Oblicz prawdopodobieństwo, że wybierając losowo z tego pojemnika 3 części, wybierzesz dokładnie dwie części z wadą
. Każda część ma tylko jedną wadę. Oblicz prawdopodobieństwo, że wybierając losowo z tego pojemnika 3 części, wybierzesz dokładnie dwie części z wadą 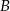 .
. 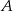 , 40 sztuk z powodu wady
, 40 sztuk z powodu wady 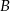 , pozostałe z powodu wady
, pozostałe z powodu wady 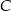 . Każda część ma tylko jedną wadę. Oblicz prawdopodobieństwo, że wybierając losowo z tego pojemnika 3 części, wybierzesz dokładnie dwie części z wadą
. Każda część ma tylko jedną wadę. Oblicz prawdopodobieństwo, że wybierając losowo z tego pojemnika 3 części, wybierzesz dokładnie dwie części z wadą 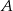 .
. 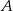 , 40 sztuk z powodu wady
, 40 sztuk z powodu wady 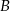 , pozostałe z powodu wady
, pozostałe z powodu wady 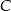 . Każda część ma tylko jedną wadę. Oblicz prawdopodobieństwo, że wybierając losowo z tego pojemnika 3 części, wybierzesz wszystkie części z tą samą jedną wadą.
. Każda część ma tylko jedną wadę. Oblicz prawdopodobieństwo, że wybierając losowo z tego pojemnika 3 części, wybierzesz wszystkie części z tą samą jedną wadą. 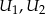 i
i 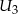 niezależnie wykrywające awarie. Prawdopodobieństwo wykrycia awarii przez kolejne urządzenia wynoszą
niezależnie wykrywające awarie. Prawdopodobieństwo wykrycia awarii przez kolejne urządzenia wynoszą 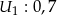 ,
, 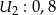 ,
, 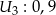 . Oblicz prawdopodobieństwo wykrycia awarii przez:
. Oblicz prawdopodobieństwo wykrycia awarii przez: 