W ostrosłupie prawidłowym sześciokątnym dany jest kąt nachylenia ściany bocznej do płaszczyzny podstawy 
. Oblicz stosunek pola podstawy do pola powierzchni bocznej ostrosłupa.
/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Prawidłowy sześciokątny
W ostrosłupie prawidłowym sześciokątnym pole przekroju płaszczyzną przechodzącą przez jego wysokość oraz przez dwie krawędzie boczne jest dwukrotnie większe od pola podstawy i wynosi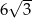 
. Oblicz odległość spodka wysokości ostrosłupa od jego krawędzi bocznej.
Wysokość ostrosłupa prawidłowego sześciokątnego jest równa 6 cm i stanowi 
długości krawędzi podstawy.
- Oblicz miarę kąta nachylenia ściany bocznej do podstawy.
- Oblicz objętość ostrosłupa
Ukryj
Podobne zadania
Wysokość ostrosłupa prawidłowego sześciokątnego jest równa 9 cm i stanowi 
długości krawędzi podstawy.
- Oblicz miarę kąta nachylenia ściany bocznej do podstawy.
- Oblicz objętość ostrosłupa.
Wysokość prawidłowego ostrosłupa sześciokątnego ma długość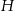 
, a krawędź podstawy ma długość 
. Wyznacz pole przekroju wyznaczonego przez krótszą przekątną podstawy i wierzchołek ostrosłupa.
Oblicz wysokość i objętość ostrosłupa prawidłowego sześciokątnego o krawędzi podstawy 4 cm i krawędzi bocznej 10 cm.
Oblicz objętość i pole powierzchni bocznej ostrosłupa prawidłowego sześciokątnego o krawędzi podstawy 2 cm i krawędzi bocznej 6 cm.
Dany jest ostrosłup prawidłowy sześciokątny. Wysokość ściany bocznej tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem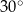 
i ma długość równą 6 (zobacz rysunek).
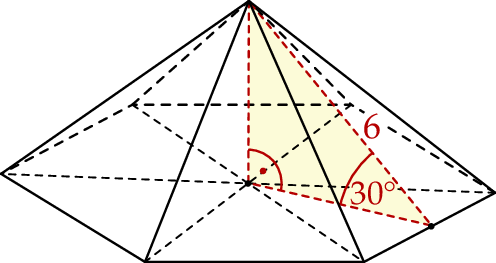
Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa.
