Ciąg 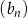 jest nieskończonym ciągiem liczb dodatnich, a ciąg
jest nieskończonym ciągiem liczb dodatnich, a ciąg 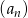 spełnia warunek
spełnia warunek
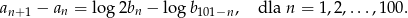
Oblicz 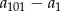 .
.
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Ciąg 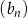 jest nieskończonym ciągiem liczb dodatnich, a ciąg
jest nieskończonym ciągiem liczb dodatnich, a ciąg 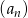 spełnia warunek
spełnia warunek
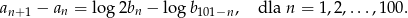
Oblicz 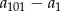 .
.
Liczba przekątnych wielokąta wypukłego, w którym jest  boków i
boków i 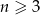 wyraża się wzorem
wyraża się wzorem 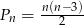 .
.
Dany jest ciąg 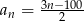 .
.
Dany jest ciąg 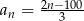 .
.
Ciąg 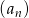 jest określony wzorem
jest określony wzorem 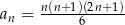 dla
dla 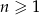 . Wykaż, że każdy kolejny wyraz tego ciągu jest większy od poprzedniego wyrazu o kwadrat liczby naturalnej.
. Wykaż, że każdy kolejny wyraz tego ciągu jest większy od poprzedniego wyrazu o kwadrat liczby naturalnej.
Ile wyrazów ciągu o wyrazie ogólnym 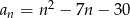 , dla
, dla 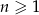 , jest liczbami ujemnymi?
, jest liczbami ujemnymi?
Ile wyrazów ujemnych ma ciąg 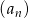 określony wzorem
określony wzorem 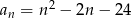 dla
dla 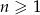 ?
?
Ile wyrazów ujemnych ma ciąg 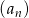 określony wzorem
określony wzorem 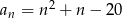 dla
dla 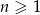 ?
?
Ile wyrazów ciągu o wyrazie ogólnym 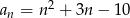 , dla
, dla 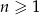 , jest liczbami ujemnymi?
, jest liczbami ujemnymi?
Ciąg 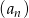 określony jest wzorem
określony jest wzorem 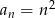 . Wyraź w zależności od
. Wyraź w zależności od  , rożnicę
, rożnicę 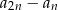 .
.
Suma 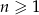 początkowych wyrazów ciągu
początkowych wyrazów ciągu 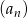 wyraża się wzorem
wyraża się wzorem 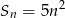 . Oblicz, ile wyrazów tego ciągu jest liczbami trzycyfrowymi.
. Oblicz, ile wyrazów tego ciągu jest liczbami trzycyfrowymi.
Wykazać, że 1 nie jest wyrazem ciągu 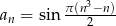 .
.
Ciąg 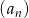 określony jest wzorem
określony jest wzorem 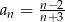 .
.
 .
.Dany jest ciąg 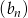 o wyrazie ogólnym
o wyrazie ogólnym 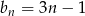 . Ile wyrazów ciągu
. Ile wyrazów ciągu 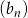 należy do przedziału
należy do przedziału 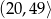 ?
?
Dany jest ciąg określony wzorem 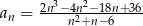 .
.
Ciąg 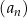 jest określony wzorem
jest określony wzorem
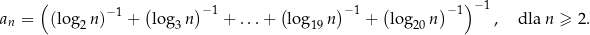
Oblicz sumę 19 początkowych wyrazów ciągu 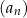 .
.
Udowodnij, że liczba 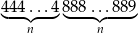 jest kwadratem liczby naturalnej.
jest kwadratem liczby naturalnej.
Naszkicuj wykres ciągu o podanych wyrazach początkowych: 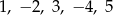 . Odgadnij wzór ogólny tego ciągu.
. Odgadnij wzór ogólny tego ciągu.
Naszkicuj wykres ciągu o podanych wyrazach początkowych: 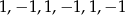 . Odgadnij wzór ogólny tego ciągu.
. Odgadnij wzór ogólny tego ciągu.
Naszkicuj wykres ciągu o podanych wyrazach początkowych: 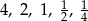 . Odgadnij wzór ogólny tego ciągu.
. Odgadnij wzór ogólny tego ciągu.
Naszkicuj wykres ciągu o podanych wyrazach początkowych: 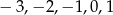 . Odgadnij wzór ogólny tego ciągu.
. Odgadnij wzór ogólny tego ciągu.
Ciąg 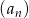 określony jest wzorem
określony jest wzorem 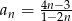 , dla
, dla 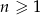 . Oblicz ile wyrazów ciągu
. Oblicz ile wyrazów ciągu 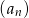 różni się od liczby -2 o więcej niż 0,1.
różni się od liczby -2 o więcej niż 0,1.
Ciąg 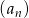 jest określony wzorem
jest określony wzorem 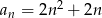 dla
dla 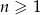 . Wykaż, że suma każdych dwóch kolejnych wyrazów tego ciągu jest kwadratem liczby naturalnej.
. Wykaż, że suma każdych dwóch kolejnych wyrazów tego ciągu jest kwadratem liczby naturalnej.
Ciąg 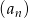 jest określony wzorem
jest określony wzorem 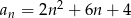 dla
dla 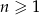 . Wykaż, że suma każdych dwóch kolejnych wyrazów tego ciągu jest kwadratem liczby naturalnej.
. Wykaż, że suma każdych dwóch kolejnych wyrazów tego ciągu jest kwadratem liczby naturalnej.
Ciąg 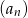 określony jest przez warunki
określony jest przez warunki 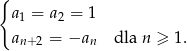
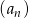 .
. 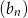 danego wzorem
danego wzorem 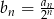 .
.Ciąg 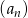 dany jest wzorem
dany jest wzorem 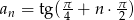 . Oblicz sumę
. Oblicz sumę 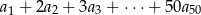 .
.
Dla każdego 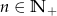 wyrazy ciągu
wyrazy ciągu 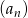 spełniają dwa warunki
spełniają dwa warunki 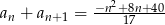 i
i 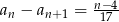 . Oblicz, które wyrazy tego ciągu są dodatnie.
. Oblicz, które wyrazy tego ciągu są dodatnie.
Dany jest ciąg 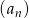 określony wzorem
określony wzorem 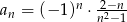 dla
dla 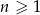 . Oblicz
. Oblicz 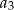 i
i 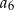 .
.
