Niech 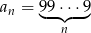 . Oblicz sumę 12 początkowych wyrazów ciągu
. Oblicz sumę 12 początkowych wyrazów ciągu 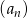 .
.
/Szkoła średnia/Ciągi/Dowolny
Niech 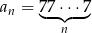 . Oblicz sumę 12 początkowych wyrazów ciągu
. Oblicz sumę 12 początkowych wyrazów ciągu 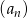 .
.
Dany jest ciąg 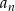 o wyrazie ogólnym
o wyrazie ogólnym 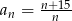 .
.
- Oblicz, ile wyrazów ciągu
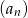 jest większych od 3.
jest większych od 3. - Wyznacz wszystkie te wyrazy ciągu
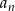 , które są liczbami naturalnymi.
, które są liczbami naturalnymi.
Dany jest ciąg 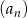 określony wzorem
określony wzorem 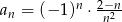 dla
dla 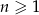 . Oblicz
. Oblicz 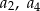 i
i 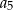 .
.
Dany jest ciąg 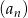 określony wzorem
określony wzorem 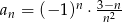 dla
dla 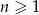 . Oblicz
. Oblicz 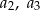 i
i 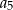 .
.
Dany jest ciąg 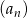 o wyrazie ogólnym
o wyrazie ogólnym 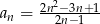 .
.
- Uzasadnij, że wszystkie wyrazy ciągu
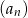 są liczbami całkowitymi.
są liczbami całkowitymi. - Który wyraz jest równy 5?
- Różnica sześcianów dwóch kolejnych wyrazów ciągu
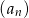 wynosi
wynosi 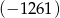 . Wyznacz te wyrazy.
. Wyznacz te wyrazy.
Nieskończony ciąg liczbowy 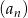 określony jest wzorem:
określony jest wzorem:
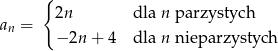
- Wyznacz sumę dwudziestu początkowych wyrazów ciągu.
- Zbadaj, czy istnieje wyraz ciągu równy 5. Odpowiedź uzasadnij.
Nieskończony ciąg liczbowy 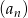 jest określony wzorem
jest określony wzorem 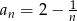 , dla
, dla 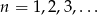 .
.
- Oblicz, ile wyrazów ciągu
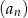 jest mniejszych od 1,975.
jest mniejszych od 1,975. - Dla pewnej liczby
 trzywyrazowy ciąg
trzywyrazowy ciąg 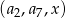 jest arytmetyczny. Oblicz
jest arytmetyczny. Oblicz  .
.
Ciąg 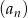 jest określony wzorem
jest określony wzorem 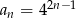 , gdzie
, gdzie 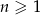 . Wyznacz wszystkie wartości
. Wyznacz wszystkie wartości 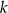 , dla których iloczyn
, dla których iloczyn 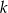 początkowych wyrazów ciągu
początkowych wyrazów ciągu 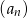 jest równy
jest równy 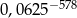 .
.
Wyrazami skończonego i malejącego ciągu 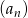 są wszystkie liczby trzycyfrowe podzielne przez 9.
są wszystkie liczby trzycyfrowe podzielne przez 9.
- Podaj ostatni wyraz tego ciągu.
- Znajdź wzór na wyraz ogólny ciągu
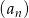 .
. - Oblicz sumę dziewiętnastu początkowych wyrazów ciągu
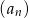 .
.
Wyznacz wszystkie wyrazy nieskończonego ciągu 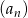 określonego wzorem
określonego wzorem 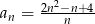 ,
, 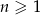 , które są liczbami całkowitymi.
, które są liczbami całkowitymi.
Średnia arytmetyczna  początkowych wyrazów ciągu
początkowych wyrazów ciągu 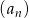 jest równa
jest równa 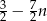 . Wyznacz wzór ogólny ciągu
. Wyznacz wzór ogólny ciągu 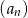 .
.
Średnia arytmetyczna  początkowych wyrazów ciągu
początkowych wyrazów ciągu 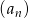 jest równa
jest równa 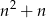 . Wyznacz wzór ogólny ciągu
. Wyznacz wzór ogólny ciągu 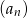 .
.
Różnica ciągu arytmetycznego 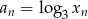 jest równa
jest równa 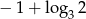 . Oblicz
. Oblicz 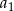 jeżeli wiadomo, że
jeżeli wiadomo, że
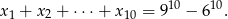
Ciąg 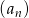 określony jest wzorem
określony jest wzorem 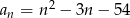 .
.
- Nie korzystając z kalkulatora, rozstrzygnij, czy 58 wyraz ciągu
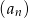 jest kwadratem liczby naturalnej.
jest kwadratem liczby naturalnej. - Znajdź takie dwa kolejne wyrazy ciągu
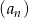 , aby ich rożnica była równa 20.
, aby ich rożnica była równa 20.
Ciąg 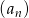 określony jest w taki sposób:
określony jest w taki sposób: 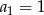 , zaś
, zaś  -ty wyraz ciągu
-ty wyraz ciągu 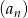 , gdy
, gdy 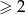 , jest największym dzielnikiem liczby
, jest największym dzielnikiem liczby  mniejszym od
mniejszym od  . Ile wyrazów ciągu
. Ile wyrazów ciągu 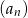 jest równych 2? Odpowiedź uzasadnij.
jest równych 2? Odpowiedź uzasadnij.
Wyraz ogólny ciągu 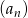 dany jest wzorem
dany jest wzorem 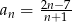 , gdzie
, gdzie 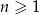 .
.
- Który wyraz ciągu
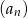 równa się
równa się 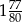 ?
? - Ile wyrazów danego ciągu należy do przedziału
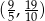 ?
? - Które wyrazy tego ciągu przyjmują wartości całkowite?
Dany jest ciąg 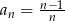 . Wyznacz wzór ogólny ciągu
. Wyznacz wzór ogólny ciągu 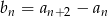 , gdzie
, gdzie 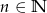 .
.
Dany jest ciąg 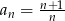 . Wyznacz wzór ogólny ciągu
. Wyznacz wzór ogólny ciągu 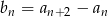 , gdzie
, gdzie 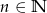 .
.
Podaj wzór na wyraz ogólny ciągu 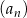 określonego w następujący sposób:
określonego w następujący sposób: 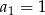 oraz ciąg
oraz ciąg 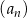 jest ciągiem kolejnych liczb naturalnych, które przy dzieleniu przez 5 dają resztę 1.
jest ciągiem kolejnych liczb naturalnych, które przy dzieleniu przez 5 dają resztę 1.
Dany jest ciąg o wyrazie ogólnym 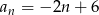 . Wybierz sto kolejnych początkowych wyrazów ciągu
. Wybierz sto kolejnych początkowych wyrazów ciągu 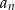 i oblicz dla jakiej liczby naturalnej
i oblicz dla jakiej liczby naturalnej 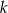 stosunek wyrazu stojącego na miejscu
stosunek wyrazu stojącego na miejscu 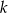 , licząc od początku, do wyrazu stojącego na miejscu
, licząc od początku, do wyrazu stojącego na miejscu 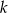 , licząc od końca, jest równy
, licząc od końca, jest równy 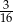 .
.
Suma  początkowych wyrazów ciągu
początkowych wyrazów ciągu 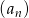 wyraża się wzorem
wyraża się wzorem 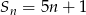 . Wyznacz wzór na
. Wyznacz wzór na  -ty wyraz ciągu
-ty wyraz ciągu 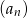 dla
dla 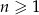 .
.
O ciągu 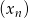 dla
dla 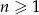 wiadomo, że:
wiadomo, że:
- ciąg
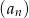 określony wzorem
określony wzorem 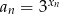 dla
dla 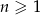 jest geometryczny o ilorazie
jest geometryczny o ilorazie 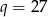 .
. 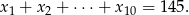
Oblicz 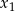 .
.
Wyznacz największy wyraz ciągu 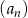 danego wzorem
danego wzorem 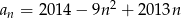 , dla
, dla 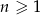 .
.

