Okrąg wpisany w trójkąt prostokątny 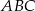 o bokach długości
o bokach długości 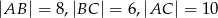 jest styczny do boków
jest styczny do boków 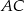 i
i 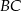 w punktach
w punktach 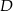 i
i 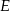 . Proste
. Proste 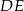 i
i 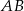 przecinają się punkcie
przecinają się punkcie 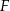 . Oblicz pole trójkąta
. Oblicz pole trójkąta 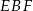 .
.
/Konkursy
Nietaktowny mężczyzna zapytał swoją sąsiadkę, ile ma lat. Sąsiadka odpowiedziała mu: „Jeśli będę żyła równa sto lat, to mój obecny wiek stanowi dwie trzecie czasu, jaki mi pozostał do przeżycia.” Ile lat ma sąsiadka?
A) 20 B) 40 C) 50 D) 60 E) 80
Liczby pierwsze 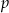 i
i 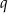 , gdzie
, gdzie 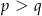 , nazywamy bliźniaczymi, jeżeli
, nazywamy bliźniaczymi, jeżeli 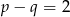 . Udowodnij, że liczby pierwsze
. Udowodnij, że liczby pierwsze 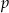 i
i 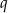 są bliźniacze wtedy i tylko wtedy, gdy
są bliźniacze wtedy i tylko wtedy, gdy 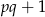 jest kwadratem liczby naturalnej.
jest kwadratem liczby naturalnej.
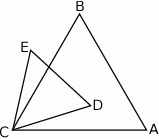
Trójkąty równoboczne 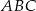 i
i 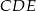 są położone tak, jak na poniższym rysunku. Wykaż, że
są położone tak, jak na poniższym rysunku. Wykaż, że 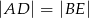 .
.
Rozważamy pary takich liczb całkowitych dodatnich 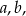 że
że 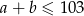 oraz
oraz 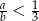 . Największy możliwy iloraz
. Największy możliwy iloraz 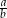 jest równy
jest równy
A) 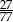 B)
B) 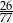 C)
C) 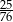 D)
D) 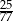 E)
E) 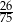
Suma cyfr sumy cyfr liczby 2008 jest równa
A) 2 B) 6 C) 8 D) 10 E) 1
Na ramionach 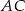 i
i 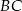 trójkąta równoramiennego
trójkąta równoramiennego 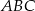 wybrano punkty
wybrano punkty 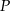 i
i 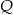 w ten sposób, że odcinek
w ten sposób, że odcinek 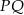 jest równoległy do podstawy
jest równoległy do podstawy 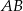 i styczny do okręgu wpisanego w trójkąt
i styczny do okręgu wpisanego w trójkąt 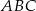 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 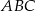 jest równe
jest równe
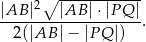
Każdy kąt trójkąta 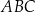 ma miarę mniejszą od
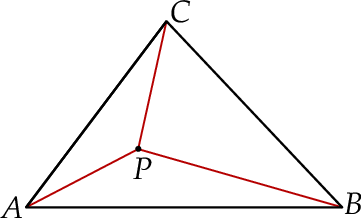
ma miarę mniejszą od 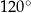 . Wyznacz taki punkt
. Wyznacz taki punkt 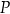 wewnątrz trójkąta
wewnątrz trójkąta 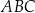 , dla którego suma
, dla którego suma 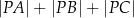 jest najmniejsza możliwa.
jest najmniejsza możliwa.
Odgadnij jakie cyfry kryją się za literami w podanym działaniu, jeżeli różnym literom odpowiadają różne cyfry.

Heron codziennie rano wyrusza ze swojego domu (punkt 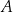 ) do brzegu rzeki (prosta
) do brzegu rzeki (prosta 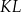 ) aby nabrać wodę (w punkcie
) aby nabrać wodę (w punkcie 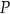 ) i podlać rośliny w sadzie (punkt
) i podlać rośliny w sadzie (punkt 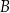 ).
).
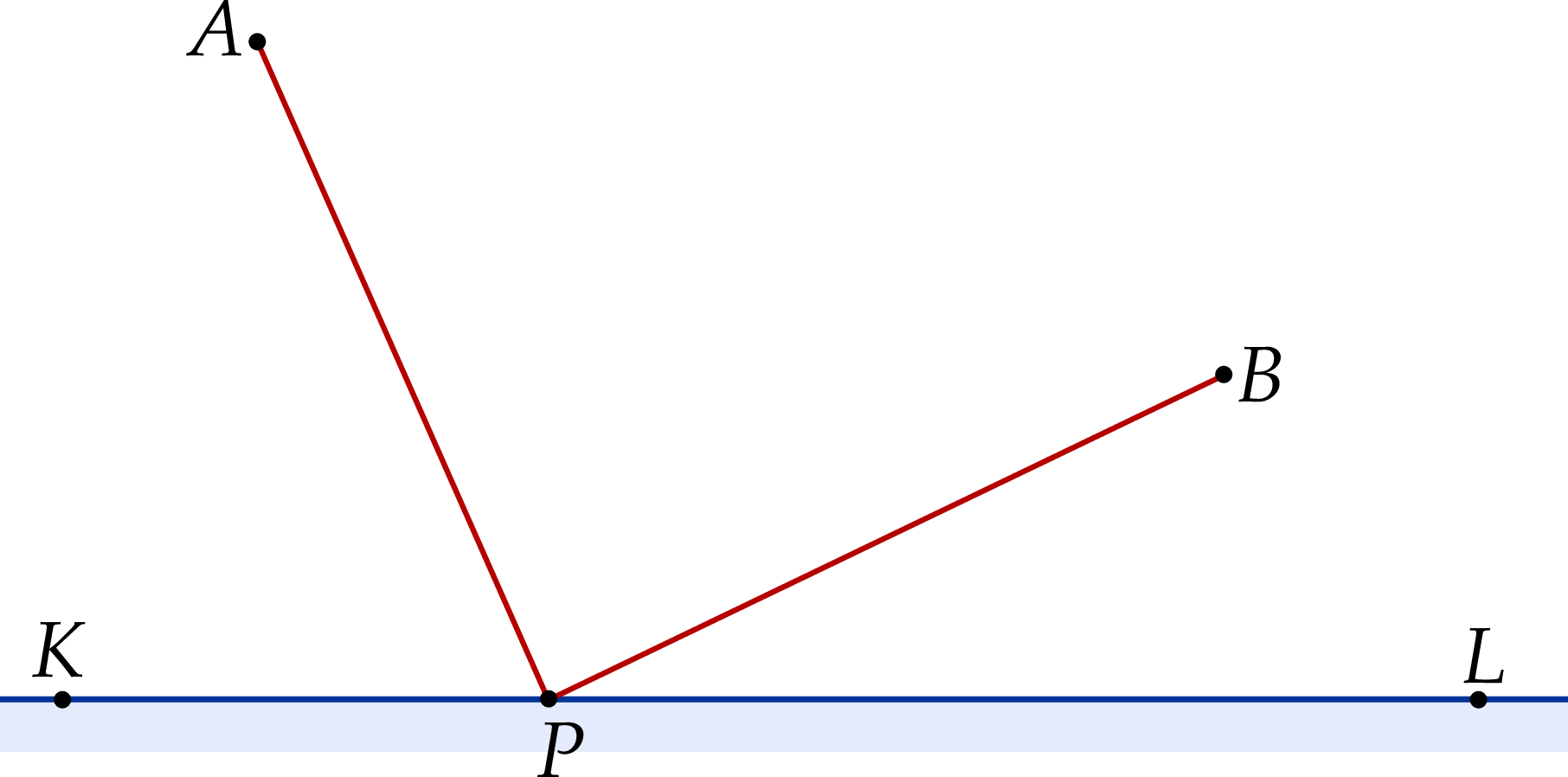
Jakie powinno być położenie punktu 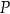 , żeby pokonana przez niego droga (wzdłuż łamanej
, żeby pokonana przez niego droga (wzdłuż łamanej 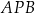 ) była najkrótsza?
) była najkrótsza?
Cztery liczby, wśród nich 2, 3, 4, rozmieszczono w polach tabeli. Wiadomo, że suma liczb w pierwszym wierszu jest równa 9, a suma liczb w drugim wierszu jest równa 6. Czwarta liczbą jest
![]()
A) 4 B) 5 C) 6 D) 7 E) 8
Wykaż, że dla każdej liczby całkowitej nieparzystej  liczba
liczba 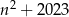 jest podzielna przez 8.
jest podzielna przez 8.
Wykaż, że jeżeli liczba  nie dzieli się przez 3, to liczba
nie dzieli się przez 3, to liczba 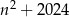 jest podzielna przez 3.
jest podzielna przez 3.
Pociąg składa się z lokomotywy (na początku składu) i pięciu wagonów oznaczonych numerami: I,II,III,IV,V. Na ile sposobów można zestawić skład tego pociągu tak, aby wagon I był bliżej lokomotywy niż wagon II?
A) 120 B) 60 C) 48 D) 30 E) 10
Na okręgu o promieniu  opisano trapez, w którym
opisano trapez, w którym 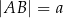 i
i 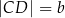 .
.
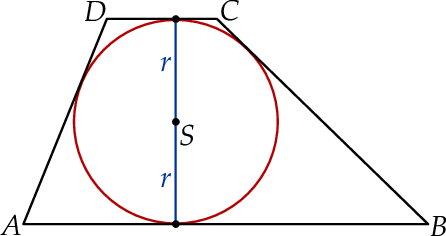
Wykaż, że 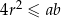 .
.
W trapezie 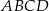 połączono środek
połączono środek 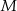 ramienia trapezu
ramienia trapezu 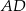 z końcami drugiego ramienia
z końcami drugiego ramienia 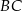 . Wykaż, że pole powstałego trójkąta
. Wykaż, że pole powstałego trójkąta 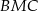 jest równe połowie pola trapezu
jest równe połowie pola trapezu 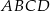 .
.
Punkt 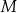 jest środkiem boku
jest środkiem boku 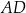 . Udowodnij, że pole trójkąta
. Udowodnij, że pole trójkąta 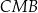 jest połową pola trapezu
jest połową pola trapezu 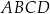 (
(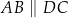 ).
).

Kwadraty przedstawione na rysunku mają boki równe 1. Pole zacieniowanego czworokąta jest równe
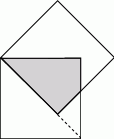
A) 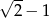 B)
B) 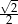 C)
C) 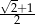 D)
D) 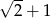 E)
E) 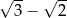
Mirek zmierzył kąty w dwóch trójkątach. Jeden z trójkątów był ostrokątny, a drugi rozwartokątny. Mirek zapamiętał miary czterech z tych katów 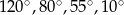 . Jaka jest miara najmniejszego kąta w trójkącie ostrokątnym?
. Jaka jest miara najmniejszego kąta w trójkącie ostrokątnym?
A) 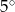 B)
B) 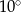 C)
C) 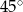 D)
D) 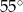 E) Nie można tego ustalić.
E) Nie można tego ustalić.
Iloczyn czterech różnych dodatnich liczb całkowitych jest równy 100. Suma tych liczb jest równa
A) 10 B) 12 C) 15 D) 18 E) 20
Udowodnij, że liczb pierwszych jest nieskończenie wiele.
Konkurs „Kangur Matematyczny” odbywa się w Europie każdego roku począwszy od 1991. W roku 2006 odbywa się on po raz
A) 15 B) 16 C) 17 D) 13 E) 14

