Z punktu 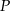 należącego do boku
należącego do boku 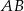 trójkąta równobocznego
trójkąta równobocznego 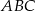 poprowadzono półprostą dzielącą trójkąt na dwie figury o równych polach. Oblicz tangens kąta jaki tworzy ta półprosta z odcinkiem
poprowadzono półprostą dzielącą trójkąt na dwie figury o równych polach. Oblicz tangens kąta jaki tworzy ta półprosta z odcinkiem 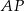 , jeśli
, jeśli 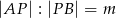 i
i 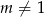 .
.
/Konkursy
Jaka jest najmniejsza wartość wyrażenia 2007–KAN–GA–ROO, w którym różnym literom odpowiadają różne cyfry?
A) 100 B) 110 C) 112 D) 119 E) 129
W gronie uczniów pewnej klasy dziewczęta stanowią więcej niż 45%, ale mniej niż 50% wszystkich uczniów. Jaka jest najmniejsza możliwa liczba dziewcząt w tej klasie?
A) 3 B) 4 C) 5 D) 6 E) 7
Wartość sumy 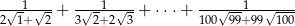 jest równa
jest równa
A) 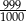 B)
B) 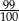 C)
C) 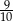 D) 9 E) 1
D) 9 E) 1
Dane są dwa półokręgi o wspólnym środku 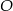 i średnicach odpowiednio
i średnicach odpowiednio 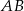 i
i 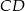 (punkty
(punkty 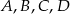 i
i 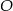 są współliniowe).
są współliniowe).
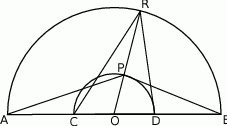
Punkt 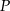 leży na wewnętrznym półokręgu, punkt
leży na wewnętrznym półokręgu, punkt 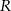 leży na zewnętrznym półokręgu, punkty
leży na zewnętrznym półokręgu, punkty 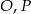 i
i 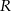 są współliniowe. Udowodnij, że
są współliniowe. Udowodnij, że 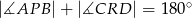 .
.
Babcia upiekła swoim wnukom paszteciki. Gdyby dała każdemu z nich po 2, to pozostałyby jej 3 paszteciki, a gdyby chciała dać każdemu z nich po 3, to zabrakłoby jej 2 pasztecików. Ilu wnuków ma babcia?
A) 2 B) 3 C) 4 D) 5 E) 6
Jeden z boków trójkąta ma długość 120, drugi 130. Która z poniższych liczb nie może być długością trzeciego boku?
A) 40 B) 99 C) 100 D) 150 E) 260
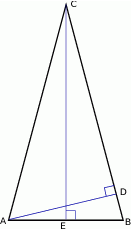
Na przyprostokątnych 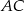 i
i 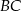 trójkąta prostokątnego
trójkąta prostokątnego 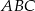 zbudowano, na zewnątrz trójkąta, kwadraty
zbudowano, na zewnątrz trójkąta, kwadraty 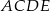 i
i 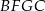 . Odcinek
. Odcinek 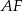 przecina przyprostokątną
przecina przyprostokątną 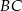 w punkcie
w punkcie 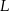 , a odcinek
, a odcinek 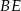 przecina przyprostokątną
przecina przyprostokątną 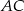 w punkcie
w punkcie 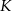 (zobacz rysunek). Udowodnij, że
(zobacz rysunek). Udowodnij, że 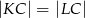 .
.
W pewnej klasie okazało się, że liczba chłopców, którzy rozwiązali zadania kangurowe, jest równa liczbie dziewcząt, które nie potrafiły tego zadania rozwiązać. Kogo było więcej w tej klasie: tych wszystkich, którzy rozwiązali zadanie, czy wszystkich dziewcząt?
A) Wszystkich dziewcząt
B) Tych wszystkich, którzy rozwiązali zadanie
C) Tych, którzy rozwiązali zadanie, było tyle samo co wszystkich dziewcząt
D) Nie da się tego ustalić
E) Opisana sytuacja jest niemożliwa
W trójkącie równoramiennym  , w którym
, w którym 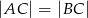 wysokość
wysokość 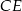 jest dwa razy dłuższa od wysokości
jest dwa razy dłuższa od wysokości 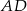 (patrz rysunek). Oblicz kosinusy wszystkich kątów wewnętrznych trójkąta
(patrz rysunek). Oblicz kosinusy wszystkich kątów wewnętrznych trójkąta 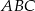 .
.
W trójkącie równobocznym 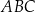 o wysokości
o wysokości 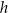 obrano punkt
obrano punkt 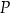 , z którego poprowadzono odcinki prostopadłe do boków tego trójkąta. Wykaż, że suma długości tych odcinków jest równa
, z którego poprowadzono odcinki prostopadłe do boków tego trójkąta. Wykaż, że suma długości tych odcinków jest równa 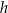 .
.
Liczba  stanowi 125% liczby
stanowi 125% liczby 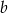 . Ile procent liczby
. Ile procent liczby  stanowi liczba
stanowi liczba 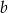 ?
?
A) 50% B) 75% C) 80% D) 90% E) 100%
Iloma zerami kończy się liczba 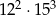 ?
?
A) 6 B) 12 C) 5 D) 3 E) 1
W spotkaniu piłkarskim drużyna gospodarzy jako pierwsza objęła prowadzenie i nie straciła go do końca meczu. Mecz zakończył się zwycięstwem gospodarzy w stosunku 5:4. Na ile sposobów mogły padać bramki w tym meczu?
A) 17 B) 13 C) 20 D) 14 E) 9
Suma cyfr pewnej liczby dwucyfrowej wynosi 12. Jeżeli od liczby utworzonej z przestawienia cyfr liczby początkowej odejemiemy 8 to otrzymamy liczbę 3 razy mniejszą od liczby początkowej. Znajdz tę liczbę.
Z przystani  w kierunku przystani
w kierunku przystani 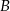 wypłynął statek, który poruszał się z prędkością 10 km/h. W cztery godziny później z tej samej miejscowości i w tym samym kierunku wypłynął drugi statek poruszający się z prędkością 12 km/h. Oba statki dotarły jednocześnie do miejscowości
wypłynął statek, który poruszał się z prędkością 10 km/h. W cztery godziny później z tej samej miejscowości i w tym samym kierunku wypłynął drugi statek poruszający się z prędkością 12 km/h. Oba statki dotarły jednocześnie do miejscowości 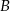 . Jaka jest odległość pomiędzy tymi przystaniami?
. Jaka jest odległość pomiędzy tymi przystaniami?
Dwa lata temu córka była 6 razy młodsza od matki, a za cztery lata matka będzie 3 razy starsza od córki. Ile lat ma teraz córka?
Przez dopisanie do siebie 20 słów KANGAROO powstał ciąg liter KANGAROOKANGAROO...KANGAROO. Na początek, w ciągu tym zmazujemy litery stojące na parzystych miejscach. Następnie, w tak otrzymanym nowym ciągu, zmazujemy litery stojące na parzystych miejscach. Postępowanie to kontynuujemy tak długo, aż pozostanie jedna litera. Jaka to litera?
A) K B) A C) N D) G E) O
Duży kwadrat o polu 1 został podzielony na kwadraty, jak na rysunku obok. Pole małego zacieniowanego kwadratu jest równe.

A) 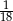 B)
B) 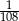 C)
C) 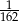 D)
D) 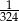 E)
E) 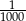
Trójkąt 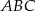 jest podstawą ostrosłupa
jest podstawą ostrosłupa 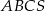 . Punkt
. Punkt 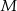 jest środkiem boku
jest środkiem boku 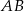 i
i 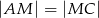 . Odcinek
. Odcinek 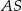 jest wysokością tego ostrosłupa. Wykaż, że kąt
jest wysokością tego ostrosłupa. Wykaż, że kąt 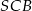 jest prosty.
jest prosty.

