Wykaż, że trójkąt, którego długości boków są trzema kolejnymi wyrazami ciągu geometrycznego, miary kątów zaś trzema kolejnymi wyrazami ciągu arytmetycznego jest trójkątem równobocznym.
/Konkursy
W prostokącie umieszczono sześć identycznych okręgów, jak na rysunku. Wierzchołki małego prostokąta są środkami czterech z tych okręgów. Wiadomo, że obwód małego prostokąta jest równy 60 cm. Ile jest równy obwód dużego prostokąta?
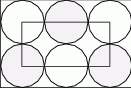
A) 90cm B) 140cm C)120 cm D)100 cm E)80 cm
Na przyprostokątnych 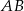 i
i 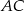 trójkąta prostokątnego równoramiennego
trójkąta prostokątnego równoramiennego 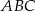 zaznaczono odpowiednio punkty
zaznaczono odpowiednio punkty 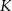 i
i 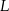 tak, że
tak, że 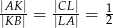 . Odcinki
. Odcinki 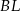 i
i 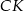 przecinają się w punkcie
przecinają się w punkcie 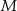 . Oblicz
. Oblicz 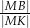 .
.
Punkty 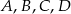 leżą na prostej w pewnym porządku. Wiadomo, że
leżą na prostej w pewnym porządku. Wiadomo, że 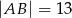 ,
, 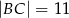 ,
, 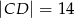 ,
, 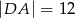 . Ile jest równa odległość pomiędzy skrajnie położonymi punktami?
. Ile jest równa odległość pomiędzy skrajnie położonymi punktami?
A) 25 B) 14 C) 38 D) 50 E) 39
Ile wynosi miara kąta ostrego w rombie, w którym długość boku jest równa średniej geometrycznej długości obu przekątnych?
A) 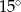 B)
B) 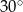 C)
C) 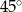 D)
D) 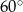 E)
E) 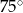
Wykaż, że jeżeli długości 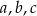 boków trójkąta spełniają równość
boków trójkąta spełniają równość
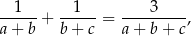
to promień okręgu opisanego na tym trójkącie jest równy 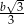 .
.
Liczba 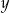 jest sumą cyfr liczby naturalnej
jest sumą cyfr liczby naturalnej  , a liczba
, a liczba  jest sumą cyfr liczby
jest sumą cyfr liczby 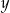 . Dla ilu liczb naturalnych
. Dla ilu liczb naturalnych  zachodzi równość
zachodzi równość 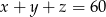 ?
?
A) 0 B) 1 C) 2 D) 3 E) Więcej niż 3
Spośród liczb wpisanych do tablicy obok wybieramy trzy liczby tak, aby żadne dwie z nich nie leżały w tym samym wierszu ani w tej samej kolumnie. Największa suma liczb w tak wybranych trójkach jest równa

A) 12 B) 15 C) 18 D) 21 E) 24
Wewnątrz trójąta 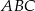 obrano punkt
obrano punkt 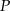 odległy od prostych
odległy od prostych 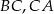 i
i 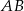 odpowiednio o
odpowiednio o 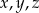 . Wykaż że
. Wykaż że
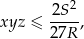
gdzie 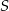 jest polem trójkąta, a
jest polem trójkąta, a 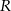 promieniem okręgu opisanego. Dla jakich punktów
promieniem okręgu opisanego. Dla jakich punktów 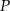 zachodzi równość?
zachodzi równość?
O godzinie 21:00 kierowca stwierdził, że jedzie z prędkością 100 km/h. Przy tej prędkości paliwa wystarczy mu na przejechanie 80 km. Najbliższa stacja paliw, gdzie może on zatankować, znajduje się w odległości 100 km. Kierowca wiedząc, że zużycie paliwa jest proporcjonalne do prędkości samochodu, postanowił w jak najkrótszym czasie dojechać do tej stacji. O której godzinie kierowca będzie na stacji?
A) 22:12 B) 22:15 C) 22:20 D) 22:25 E) 22:30
Turysta wybrał się na pieszą wędrówkę, składającą się najpierw z odcinka płaskiego, a następnie z krótkiej wspinaczki. Po dojściu do celu wrócił tą samą drogą, tzn. najpierw zszedł w dół, a potem ponownie przebył płaski odcinek. Cała wędrówka trwała 2 godziny. Ile kilometrów przewędrował jeśli wiadomo, że po płaskim terenie poruszał się z prędkością 4 km/h, wspinał się z prędkością 3 km/h, a schodził w dół z prędkością 6 km/h?
A) Za mało informacji, aby to obliczyć B) 6 km C) 7,5 km D) 8 km E) 10 km
Odcinki 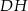 i
i 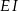 są równoległe do boku
są równoległe do boku 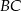 trójkąta
trójkąta 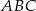 , a odcinki
, a odcinki 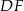 i
i 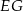 są równoległe do boku
są równoległe do boku 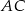 . Uzasadnij, że jeżeli
. Uzasadnij, że jeżeli 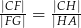 , to
, to 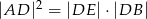 .
.
Na poniższym rysunku w pierwszym wierszu umieszczono 11 kart i na każdej z nich 2 litery.

Drugi wiersz powstał z pierwszego przez zmianę kolejności niektórych kart, przy czym nie ujawniono dolnych liter. Który z poniższych układów liter może wystapić w dolnej linii drugiego wiersza?
A) ANJAMKILIOR
B) RLIIMKOJNAA
C) JANAMKILIRO
D) RAONJMILIKA
E) ANMAIKOLIRJ
Wykaż, że jeżeli między współczynnikami trójmianów 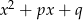 i
i 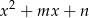 zachodzi związek
zachodzi związek 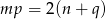 , to przynajmniej jedno z równań
, to przynajmniej jedno z równań 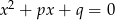 lub
lub 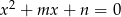 ma rozwiązanie.
ma rozwiązanie.
Proste zawierające cięciwy 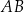 i
i 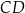 okręgu
okręgu  przecinają się w punkcie
przecinają się w punkcie 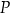 , który nie należy do okręgu
, który nie należy do okręgu  . Wykaż, że
. Wykaż, że
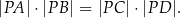
(Jest to tzw. twierdzenie o siecznych okręgu.)
W równości 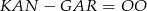 każda litera oznacza pewną cyfrę (różne litery odpowiadają różnym cyfrom). Jaka jest największa możliwa wartość liczby
każda litera oznacza pewną cyfrę (różne litery odpowiadają różnym cyfrom). Jaka jest największa możliwa wartość liczby 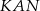 ?
?
A) 987 B) 876 C) 865 D) 864 E) 785
Ile liczb trzycyfrowych ma sumę cyfr równą 4?
A) 11 B) 6 C) 9 D) 8 E) 10
Grzyby w lesie zawierają 90% wody w swojej masie, a po wysuszeniu zawierają 15% wody w swojej masie . Oblicz ile trzeba zebrać grzybów aby uzyskać 0,5 kg suszonych grzybów.
Wielomian 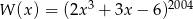 , po wykonaniu potęgowania i dokonaniu redukcji wyrazów podobnych, zapisano w postaci
, po wykonaniu potęgowania i dokonaniu redukcji wyrazów podobnych, zapisano w postaci 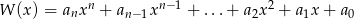 . Oblicz sumę
. Oblicz sumę 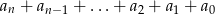 .
.
Trzy okręgi o promieniach 2, 4 i 6 są parami zewnętrznie styczne. Oblicz długość promienia okręgu zawierającego punkty styczności tych okręgów.

