Podstawy trapezu mają długości  i
i 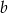 (
(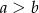 ). Suma miar kątów wewnętrznych przy dłuższej podstawie wynosi
). Suma miar kątów wewnętrznych przy dłuższej podstawie wynosi 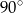 . Oblicz długość odcinka łączącego środki podstaw trapezu.
. Oblicz długość odcinka łączącego środki podstaw trapezu.
/Konkursy
Wykaż, że jeśli  jest liczbą nieparzystą, to liczba
jest liczbą nieparzystą, to liczba 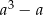 jest podzielna przez 12.
jest podzielna przez 12.
Wykaż, że dla każdej liczby naturalnej 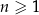 liczba
liczba 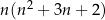 jest podzielna przez 6.
jest podzielna przez 6.
Wykaż, że dla każdej liczby całkowitej  liczba
liczba 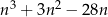 jest podzielna przez 6.
jest podzielna przez 6.
Wykaż, że dla każdej liczby naturalnej 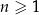 liczba
liczba 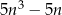 jest podzielna przez 30.
jest podzielna przez 30.
Dane są dwa zbiory liczb czterocyfrowych: zbiór 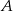 tych liczb, których iloczyn cyfr jest równy 25, oraz zbiór
tych liczb, których iloczyn cyfr jest równy 25, oraz zbiór 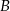 tych liczb, których iloczyn cyfr jest równy 15. Do którego zbioru należy więcej liczb i ile razy więcej liczb jest w tym zbiorze?
tych liczb, których iloczyn cyfr jest równy 15. Do którego zbioru należy więcej liczb i ile razy więcej liczb jest w tym zbiorze?
A) Zbiór 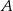 ma
ma  razy więcej elementów niż zbiór
razy więcej elementów niż zbiór 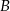 .
.
B) Zbiór 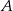 ma 2 razy więcej elementów niż zbiór
ma 2 razy więcej elementów niż zbiór 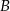 .
.
C) Zbiór 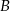 ma
ma 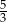 razy więcej elementów niż zbiór
razy więcej elementów niż zbiór 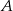 .
.
D) Zbiór 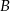 ma 2 razy więcej elementów niż zbiór
ma 2 razy więcej elementów niż zbiór 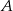 .
.
E) Oba zbiory mają po tyle samo elemantów
Wykaż, że jeżeli wielomian 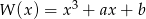 ma pierwiastek dwukrotny, to
ma pierwiastek dwukrotny, to 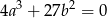 .
.
Pewien chłopiec w czwartki i piątki zawsze mówi prawdę, we wtorki zawsze kłamie, a w pozostałe dni tygodnia udziela odpowiedzi losowo, to znaczy czasem kłamie, a czasem mówi prawdę. Przez siedem kolejnych dni pytano go, jak ma na imię. Podczas pierwszych sześciu dni chłopiec udzielił następujących odpowiedzi, w takiej oto kolejności: Jan , Robert, Jan, Robert, Piotr, Robert. Jakiej odpowiedzi udzielił siódmego dnia?
A) Jan B) Robert C) Piotr D) Kasia E) Inna odpowiedź
Bieg maratoński rozgrywany jest na dystansie 42,196 km. Jarek wystartował do tego biegu o godzinie 13:37, a do mety dobiegł o godzinie 16:18. W ciągu ilu minut Jarek pokonał tę trasę?
A) 131 B) 91 C) 151 D) 185 E) 161
Na osi liczbowej zaznaczono liczby 2006 i 6002. Liczbą jednakowo odległą od nich jest
A) 3998 B) 4000 C) 4002 D) 4004 E) 4006
Wykaż, że dla dowolnych dodatnich liczb rzeczywistych  i
i 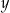 prawdziwa jest nierówność
prawdziwa jest nierówność
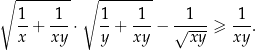
Kangurowa maszyna licząca może wykonać następujące operacje: pomnożyć daną liczbę przez 2 lub przez 3 albo podnieść daną liczbę do potęgi drugiej lub trzeciej. Którą z poniższych liczb możemy otrzymać, jeżeli maszyna rozpocznie działanie na liczbie 15 i wykona 5 operacji, kolejno na otrzymanych wcześniej wynikach?
A) 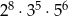 B)
B) 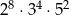 C)
C) 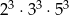 D)
D) 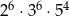 E)
E) 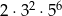
Liczbę pierwszą nazywamy specjalną jeżeli jest jednocyfrową liczbą pierwszą albo liczbą pierwszą o większej liczbie cyfr, ale taką, że po skreśleniu dowolnej skrajnej cyfry zawsze otrzymamy specjalną liczbę pierwszą. Ile jest specjalnych liczb pierwszych?
A) 4 B) 7 C) 8 D) 9 E) 11
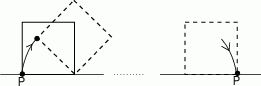
Kwadrat o boku długości 10 „toczymy” bez poślizgu wzdłuż prostej (patrz rysunek) tak długo, aż punkt 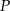 ponownie znajdzie się na tej prostej. Jaka jest długość drogi, którą zakreślił punkt
ponownie znajdzie się na tej prostej. Jaka jest długość drogi, którą zakreślił punkt 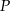 ?
?
A) 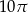 B)
B) 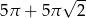 C)
C) 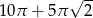 D)
D) 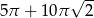 E)
E) 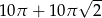
Ile razy od godziny 00:00 do godziny 23:59 zegarek elektroniczny pokaże wszystkie cyfry 2, 0, 0, 6 (w dowolnej kolejności)?
A) 2 B) 4 C) 5 D) 6 E) 12
Podstawy trapezu 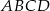 mają długości
mają długości 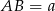 i
i 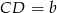 . Na ramionach trapezu wybrano punkty
. Na ramionach trapezu wybrano punkty 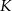 i
i 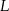 w ten sposób, że odcinek
w ten sposób, że odcinek 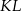 jest równoległy do podstaw oraz
jest równoległy do podstaw oraz 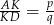 . Oblicz długość odcinka
. Oblicz długość odcinka 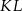 .
.
W maratonie ulicznym udział wzięło 2009 zawodników. Liczba zawodników pokonanych przez Piotra, startującego w tym maratonie, okazała się trzy razy większa niż liczba zawodników, z którymi Piotr przegrał. Które miejsce zajął Piotr w tym maratonie?
A) 503 B) 501 C) 500 D) 1503 E) 1507
Która z poniższych liczb jest największa?
A) 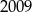 B)
B) 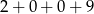 C)
C) 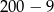 D)
D) 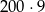 E)
E) 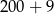
Uzasadnij, że dla każdej liczby całkowitej 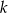 liczba
liczba 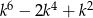 jest podzielna przez 36.
jest podzielna przez 36.
Odcinek 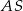 jest środkową trójkąta
jest środkową trójkąta 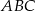 . Udowodnij, że
. Udowodnij, że 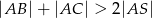 .
.
Z punktu 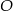 będącego środkiem kwadratu
będącego środkiem kwadratu 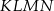 (patrz rysunek) prowadzimy odcinki
(patrz rysunek) prowadzimy odcinki 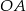 ,
, 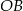 ,
, 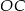 i
i 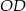 do boków tak, że
do boków tak, że 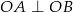 i
i 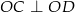 . Ile jest równe pole zacieniowanej części kwadratu, jeśli bok kwadratu ma długość 2?
. Ile jest równe pole zacieniowanej części kwadratu, jeśli bok kwadratu ma długość 2?
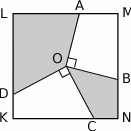
A) 1 B) 2 C) 2,5 D) 2,25 E) zależy od wyboru punktów B i C
W każdym z siedmiu kolejnych lat, zawsze 27 marca, urodził się jeden krasnoludek. Trzy najmłodsze krasnoludki mają razem 42 lata. Ile lat mają razem trzy najstarsze?
A) 51 B) 54 C) 57 D) 60 E) 63
Okrąg wpisany w trójkąt 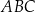 jest styczny do boków
jest styczny do boków 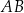 i
i 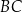 w punktach
w punktach 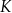 i
i 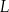 odpowiednio. Na bokach
odpowiednio. Na bokach 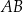 i
i 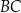 tego trójkąta wybrano punkty
tego trójkąta wybrano punkty 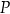 i
i 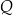 w ten sposób, że odcinek
w ten sposób, że odcinek 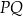 jest styczny do okręgu wpisanego w trójkąt
jest styczny do okręgu wpisanego w trójkąt 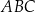 (zobacz rysunek).
(zobacz rysunek).

Wykaż, że jeżeli 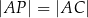 ,
, 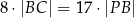 i
i 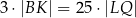 , to trójkąt
, to trójkąt 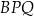 jest rozwartokątny.
jest rozwartokątny.

