Z parametrem/Wykładnicze - zadania z matematyki

/Szkoła średnia/Równania/Wykładnicze/Z parametrem

Wyznacz wszystkie wartości 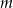, dla których równanie 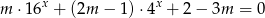m ⋅16x + (2m − 1)⋅4x + 2 − 3m = 0 nie ma pierwiastków rzeczywistych.

Dla jakich wartości parametru 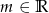m ∈ R równanie 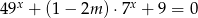x x 49 + (1 − 2m )⋅ 7 + 9 = 0 ma dwa różne rozwiązania?

Ukryj Podobne zadania

Dla jakich wartości parametru 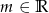m ∈ R równanie 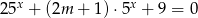x x 25 + (2m + 1)⋅ 5 + 9 = 0 ma dwa różne rozwiązania?

Znajdź zbiór tych wartości parametru 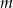dla których równanie 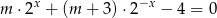m ⋅2x + (m + 3) ⋅2−x − 4 = 0 ma co najmniej jedno rozwiązanie.

Określ funkcję która każdemu argumentowi 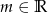m ∈ R przyporządkowuje liczbę rozwiązań równania

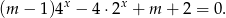
(m − 1)4x − 4 ⋅2x + m + 2 = 0.

Naszkicuj wykres tej funkcji.

Dane jest równanie 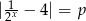-1 |2x − 4| = p z parametrem 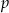. Wyznacz liczbę rozwiązań tego równania w zależności od parametru .

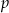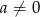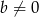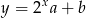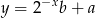Jaki warunek muszą spełniać liczby rzeczywiste a ⁄= 0 i b ⁄= 0 , aby wykresy funkcji y = 2xa + b i y = 2−xb + a miały dokładnie jeden punkt wspólny.

Dla jakich wartości parametru 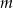równanie 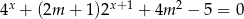x x+ 1 2 4 + (2m + 1)2 + 4m − 5 = 0 nie ma rozwiązań?

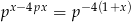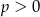Przeprowadź dyskusję liczby rozwiązań równania x−4px −4(1+x) p = p w zależności od parametru p > 0 .