Suma kwadratów długości trzech boków trójkąta prostokątnego jest równa 162. Zatem przeciwprostokątna może mieć długość:
A) 12 B) 81 C) 54 D) 9
/Szkoła średnia/Zadania testowe
Suma kwadratów długości trzech boków trójkąta prostokątnego jest równa 98. Zatem przeciwprostokątna ma długość:
A) 49 B) 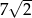 C) 7 D) 9
C) 7 D) 9
Dany jest prostopadłościan 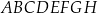 , w którym podstawy
, w którym podstawy 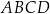 i
i 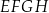 są kwadratami o boku długości 6. Przekątna
są kwadratami o boku długości 6. Przekątna 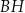 tego prostopadłościanu tworzy z przekątną
tego prostopadłościanu tworzy z przekątną 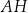 ściany bocznej
ściany bocznej 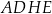 kąt o mierze
kąt o mierze 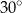 (zobacz rysunek).
(zobacz rysunek).
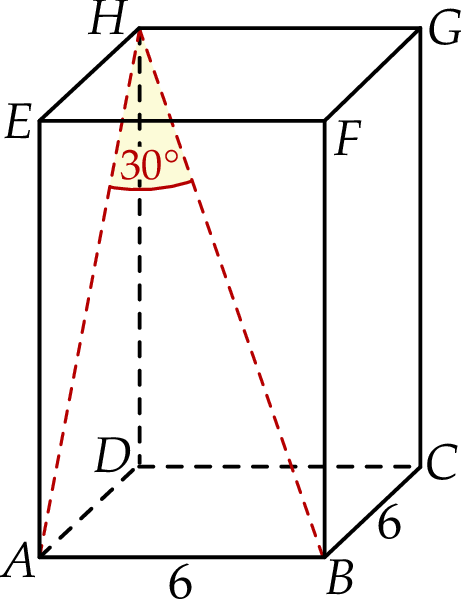
Przekątna 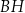 tego prostopadłościanu ma długość równą
tego prostopadłościanu ma długość równą
A) 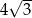 B)
B) 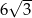 C) 12 D)
C) 12 D) 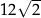
Pierwszy wyraz ciągu arytmetycznego jest równy 5, a suma jego pięciu początkowych wyrazów wynosi 55. Czwarty wyraz tego ciągu jest równy
A) 12 B) 13 C) 14 D) 15
Pierwszy wyraz ciągu arytmetycznego wynosi 7, suma siedmiu początkowych wyrazów ciągu jest równa 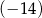 . Czwarty wyraz ciągu jest równy
. Czwarty wyraz ciągu jest równy
A) 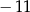 B)
B) 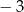 C)
C) 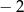 D) 16
D) 16
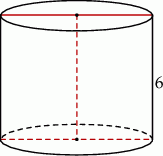
Przekrój osiowy walca jest kwadratem o boku długości 6. Objętość tego walca jest równa
A) 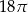 B)
B) 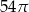 C)
C) 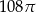 D)
D) 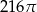
Przekrój osiowy walca jest kwadratem o boku 10. Objętość tego walca jest równa
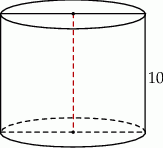
A) 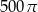 B)
B) 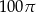 C)
C) 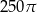 D)
D) 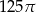
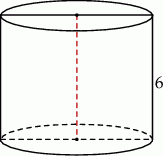
Przekrój osiowy walca jest kwadratem o boku długości 6. Objętość tego walca jest równa
A) 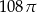 B)
B) 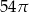 C)
C) 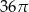 D)
D) 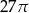
Przekrój osiowy walca jest kwadratem o boku długości 8. Objętość tego walca jest równa
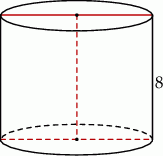
A) 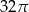 B)
B) 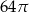 C)
C) 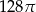 D)
D) 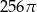
Jeżeli przekrój osiowy walca jest kwadratem o boku 4, to objętość walca jest równa
A) 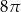 B)
B) 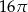 C)
C) 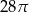 D)
D) 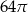
Punkt 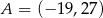 i środek
i środek 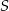 odcinka
odcinka 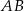 są położone symetrycznie względem początku układu współrzędnych. Zatem punkt
są położone symetrycznie względem początku układu współrzędnych. Zatem punkt 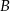 ma współrzędne
ma współrzędne
A) 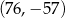 B)
B) 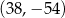 C)
C) 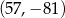 D)
D) 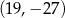
Punkt 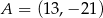 i środek
i środek  odcinka
odcinka  są położone symetrycznie względem początku układu współrzędnych. Zatem punkt
są położone symetrycznie względem początku układu współrzędnych. Zatem punkt 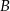 ma współrzędne
ma współrzędne
A) 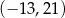 B)
B) 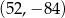 C)
C) 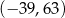 D)
D) 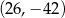
Dane są punkty 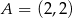 ,
, 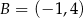 ,
, 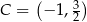 i
i 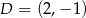 . Pole czworokąta
. Pole czworokąta 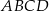 jest równe
jest równe
A) 10,5 B) 16,5 C) 9 D) 8,25
Stosunek pól powierzchni dwóch kul jest równy 1:9. Wobec tego stosunek objętości tych kul jest równy
A) 1:3 B) 1:9 C) 1:27 D) 1:81
Stosunek pól powierzchni dwóch kul jest równy 1:16. Wobec tego stosunek objętości tych kul jest równy
A) 1:256 B) 1:64 C) 1:16 D) 1:4
Stosunek pól powierzchni dwóch kul jest równy 1:4. Wobec tego stosunek objętości tych kul jest równy
A) 1:2 B) 1:8 C) 1:4 D) 1:16
Jeśli promień kuli zwiększymy o 30%, to pole powierzchni kuli wzrośnie o:
A) 30% B) 60% C) 69% D) ponad 100%
Jeśli promień kuli zmniejszymy o 50%, to pole powierzchni kuli zmaleje o:
A) 30% B) 60% C) 75% D) ponad 90%
Jeśli promień kuli zwiększymy o 50%, to pole powierzchni kuli wzrośnie o:
A) 30% B) 60% C) 69% D) ponad 100%
Automat biletowy drukuje 30 biletów w ciągu 2 minut i 6 sekund. Który wzór opisuje zależność między liczbą wydrukowanych biletów ( ), a czasem ich druku w sekundach (
), a czasem ich druku w sekundach ( ), jeżeli tempo drukowania biletów nie ulega zmianie?
), jeżeli tempo drukowania biletów nie ulega zmianie?
A) 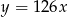 B)
B) 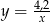 C)
C) 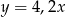 D)
D) 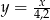
Jeżeli odcinek 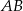 podzielimy na 80 równych części, to każda część ma długość 0,15 cm. Który wzór opisuje zależność między liczbą równych części (
podzielimy na 80 równych części, to każda część ma długość 0,15 cm. Który wzór opisuje zależność między liczbą równych części ( ), na którą dzielimy odcinek
), na którą dzielimy odcinek 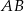 , a długością (
, a długością (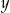 ) jednej takiej części w milimetrach?
) jednej takiej części w milimetrach?
A) 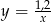 B)
B) 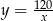 C)
C) 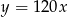 D)
D) 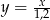
Ciąg 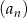 jest ciągiem geometrycznym o ilorazie
jest ciągiem geometrycznym o ilorazie 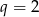 , w którym
, w którym 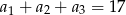 . Suma
. Suma 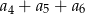 jest równa
jest równa
A) 136 B) 68 C) 34 D) 289
Ciąg 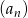 jest ciągiem geometrycznym o ilorazie
jest ciągiem geometrycznym o ilorazie 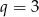 , w którym
, w którym 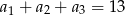 . Suma
. Suma 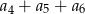 jest równa
jest równa
A) 39 B) 351 C) 117 D) 507
Odległość między środkami stycznych wewnętrznie okręgów o promieniach  i
i 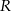 jest równa 7. Odległość między środkami stycznych zewnętrznie okręgów o promieniach
jest równa 7. Odległość między środkami stycznych zewnętrznie okręgów o promieniach  i
i 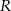 jest równa 23. Promienie
jest równa 23. Promienie  i
i 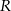 mają długości
mają długości
A) 6 i 17 B) 11 i 12 C) 10 i 13 D) 8 i 15
Wyrażenie 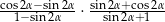 , gdzie
, gdzie  jest kątem ostrym, jest równe
jest kątem ostrym, jest równe
A) 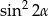 B)
B) 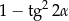 C)
C) 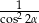 D)
D) 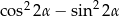
W trójkącie prostokątnym przeciwprostokątna ma długość 3, a długość przyprostokątnej leżącej naprzeciwko kąta  jest równa
jest równa 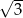 . Zatem
. Zatem
A) 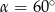 B)
B) 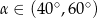 C)
C) 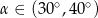 D)
D) 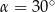
W trójkącie prostokątnym przeciwprostokątna ma długość 3, a długość przyprostokątnej leżącej naprzeciwko kąta  jest równa
jest równa 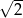 . Zatem
. Zatem
A) 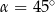 B)
B) 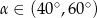 C)
C) 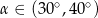 D)
D) 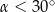
Pole rombu o kącie ostrym 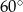 jest równe
jest równe 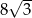 . Bok tego rombu ma długość
. Bok tego rombu ma długość
A) 6 B) 2 C) 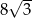 D) 4
D) 4
Pole rombu o kącie ostrym 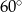 jest równe
jest równe 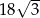 . Bok tego rombu ma długość
. Bok tego rombu ma długość
A) 9 B) 3 C) 6 D) 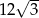
Funkcje 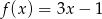 i
i 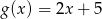 przyjmują równą wartość dla
przyjmują równą wartość dla
A) 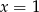 B)
B) 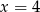 C)
C) 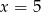 D)
D) 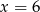
Funkcje 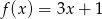 i
i 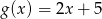 przyjmują równą wartość dla
przyjmują równą wartość dla
A) 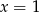 B)
B) 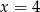 C)
C) 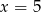 D)
D) 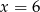
Funkcje 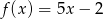 i
i 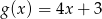 przyjmują równą wartość dla
przyjmują równą wartość dla
A) 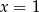 B)
B) 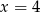 C)
C) 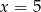 D)
D) 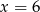
Funkcje 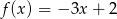 i
i 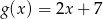 przyjmują równą wartość dla
przyjmują równą wartość dla
A) 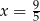 B)
B) 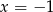 C)
C) 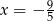 D)
D) 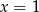
Długości boków trójkąta wychodzących z wierzchołka kąta ostrego  wynoszą odpowiednio 2 dm i 40 cm. Jaką miarę ma kąt
wynoszą odpowiednio 2 dm i 40 cm. Jaką miarę ma kąt  , jeśli pole tego trójkąta jest równe
, jeśli pole tego trójkąta jest równe 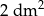 ?
?
A) 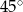 B)
B) 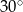 C)
C) 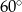 D)
D) 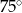
Z pudełka zawierającego dwa rodzaje monet wybieramy losowo dwie. Prawdopodobieństwo wybrania co najmniej jednej monety dwuzłotowej jest równe 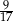 , a prawdopodobieństwo wybrania co najmniej jednej monety pięciozłotowej jest równe
, a prawdopodobieństwo wybrania co najmniej jednej monety pięciozłotowej jest równe 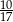 . Zatem prawdopodobieństwo wybrania dokładnie jednej monety dwuzłotowej jest równe
. Zatem prawdopodobieństwo wybrania dokładnie jednej monety dwuzłotowej jest równe
A) 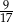 B)
B) 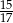 C)
C) 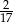 D)
D) 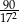
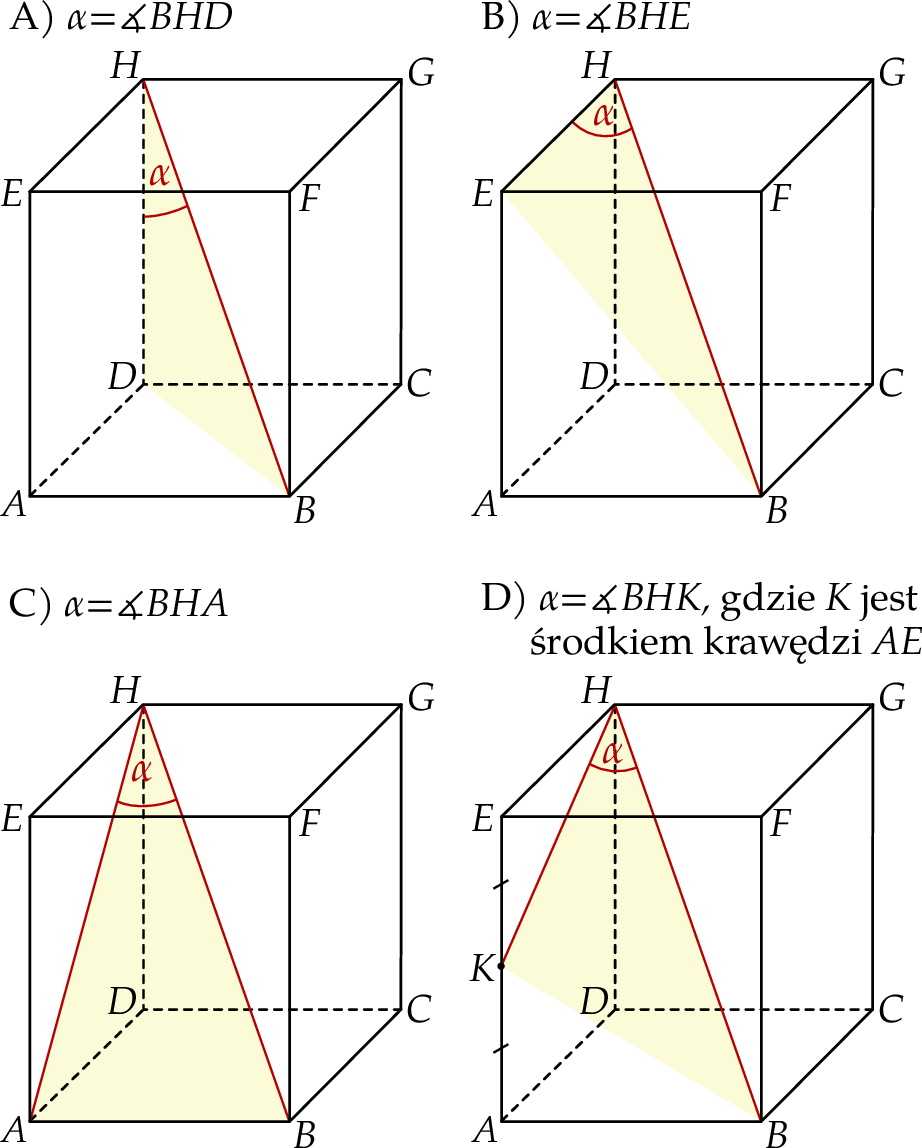
Dany jest prostopadłościan 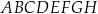 , w którym prostokąty
, w którym prostokąty 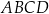 i
i 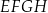 są jego podstawami. Odcinek
są jego podstawami. Odcinek 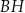 jest przekątną tego prostopadłościanu. Na którym rysunku prawidłowo oznaczono i podpisano kąt
jest przekątną tego prostopadłościanu. Na którym rysunku prawidłowo oznaczono i podpisano kąt  pomiędzy przekątną
pomiędzy przekątną 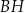 prostopadłościanu a jego ścianą boczną
prostopadłościanu a jego ścianą boczną 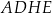 ?
?
Dany jest graniastosłup prawidłowy czworokątny, w którym krawędź podstawy ma długość 15. Przekątna graniastosłupa jest nachylona do płaszczyzny podstawy pod  takim, że
takim, że 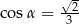 . Długość przekątnej tego graniastosłupa jest równa
. Długość przekątnej tego graniastosłupa jest równa
A) 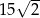 B) 45 C)
B) 45 C) 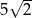 D) 10
D) 10
Dany jest graniastosłup prawidłowy czworokątny, w którym krawędź podstawy ma długość 12. Przekątna graniastosłupa jest nachylona do płaszczyzny podstawy pod  takim, że
takim, że 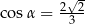 . Długość przekątnej tego graniastosłupa jest równa
. Długość przekątnej tego graniastosłupa jest równa
A) 18 B) 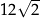 C)
C) 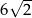 D) 8
D) 8
Liczba 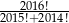 jest równa
jest równa
A) 2015 B) 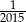 C) 1 D) 2016
C) 1 D) 2016

