Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej 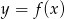 .
.
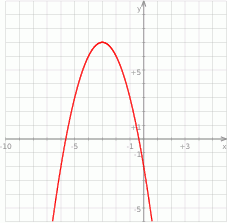
Zbiorem wartości funkcji 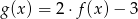 jest przedział
jest przedział
A) 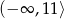 B)
B) 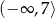 C)
C) 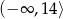 D)
D) 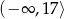
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej 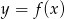 .
.

Zbiorem wartości funkcji 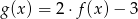 jest przedział
jest przedział
A) 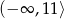 B)
B) 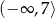 C)
C) 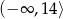 D)
D) 
Na rysunku przedstawiono fragment paraboli będącej wykresem funkcji kwadratowej 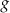 . Wierzchołkiem tej paraboli jest punkt
. Wierzchołkiem tej paraboli jest punkt 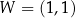 .
.
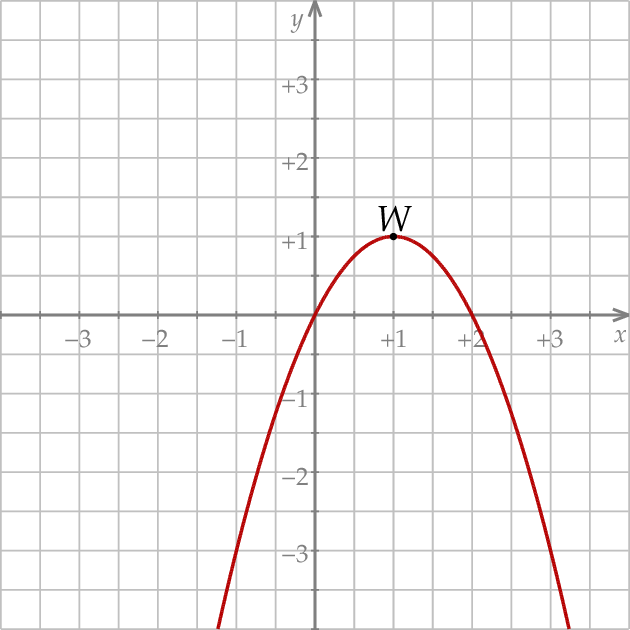
Zbiorem wartości funkcji 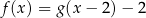 jest przedział
jest przedział
A) 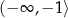 B)
B) 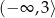 C)
C) 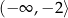 D)
D) 
Na rysunku przedstawiony jest fragment paraboli będącej wykresem funkcji kwadratowej 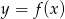 . Wierzchołkiem tej paraboli jest punkt
. Wierzchołkiem tej paraboli jest punkt 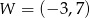 .
.
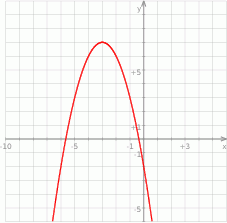
Największa wartość funkcji 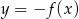 w przedziale
w przedziale 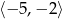 jest równa
jest równa
A) 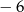 B)
B) 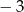 C) 7 D)
C) 7 D) 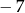
Ciąg 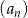 określony jest wzorem
określony jest wzorem 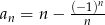 , gdzie
, gdzie 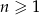 . Suma trzech początkowych wyrazów tego ciągu jest równa
. Suma trzech początkowych wyrazów tego ciągu jest równa
A) 7 B) 6 C) 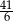 D)
D) 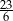
Ciąg 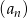 określony jest wzorem
określony jest wzorem 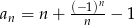 , gdzie
, gdzie 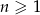 . Suma trzech początkowych wyrazów tego ciągu jest równa
. Suma trzech początkowych wyrazów tego ciągu jest równa
A) 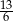 B) 6 C)
B) 6 C) 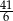 D)
D) 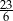
Ciąg 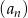 określony jest wzorem
określony jest wzorem 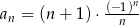 , gdzie
, gdzie 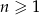 . Suma trzech początkowych wyrazów tego ciągu jest równa
. Suma trzech początkowych wyrazów tego ciągu jest równa
A) 3 B)  C)
C)  D)
D) 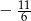
W trapezie prostokątnym kąt ostry ma miarę 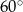 , a podstawy mają długości 6 i 9. Wysokość tego trapezu jest równa
, a podstawy mają długości 6 i 9. Wysokość tego trapezu jest równa
A) 6 B) 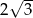 C)
C) 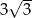 D)
D) 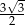
W trapezie prostokątnym kąt ostry ma miarę 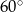 , a podstawy mają długości 10 i 8. Wysokość tego trapezu jest równa
, a podstawy mają długości 10 i 8. Wysokość tego trapezu jest równa
A) 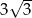 B) 4 C)
B) 4 C) 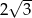 D)
D) 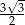
W trapezie prostokątnym kąt ostry ma miarę 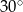 , a podstawy mają długości 8 i 10. Wysokość tego trapezu jest równa
, a podstawy mają długości 8 i 10. Wysokość tego trapezu jest równa
A) 4 B) 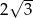 C)
C) 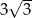 D)
D) 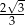
W trapezie prostokątnym kąt ostry ma miarę 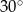 , a podstawy mają długości 6 i 9. Wysokość tego trapezu jest równa
, a podstawy mają długości 6 i 9. Wysokość tego trapezu jest równa
A) 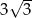 B)
B) 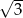 C) 6 D)
C) 6 D) 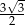
Ze zbioru liczb 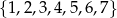 losujemy kolejno dwa razy po jednej cyfrze bez zwracania. Zapisując wylosowane cyfry w kolejności losowania, otrzymujemy liczbę dwucyfrową. Prawdopodobieństwo otrzymania liczby większej od 32 jest równe
losujemy kolejno dwa razy po jednej cyfrze bez zwracania. Zapisując wylosowane cyfry w kolejności losowania, otrzymujemy liczbę dwucyfrową. Prawdopodobieństwo otrzymania liczby większej od 32 jest równe
A) 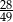 B)
B) 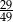 C)
C) 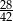 D)
D) 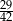
Ze zbioru cyfr 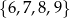 losujemy kolejno bez zwracania dwie cyfry i tworzymy liczbę dwucyfrową. Prawdopodobieństwo tego, że utworzona liczba będzie nie mniejsza niż 89 jest równe
losujemy kolejno bez zwracania dwie cyfry i tworzymy liczbę dwucyfrową. Prawdopodobieństwo tego, że utworzona liczba będzie nie mniejsza niż 89 jest równe
A) 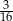 B)
B)  C)
C) 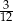 D)
D) 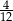
Dany jest zbiór 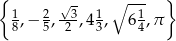 . Ile liczb należących do zbioru
. Ile liczb należących do zbioru 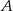 ma rozwinięcie dziesiętne skończone lub nieskończone okresowe?
ma rozwinięcie dziesiętne skończone lub nieskończone okresowe?
A) 2 B) 3 C) 4 D) 5
Dany jest zbiór 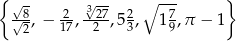 . Ile liczb należących do zbioru
. Ile liczb należących do zbioru 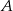 ma rozwinięcie dziesiętne skończone lub nieskończone okresowe?
ma rozwinięcie dziesiętne skończone lub nieskończone okresowe?
A) 5 B) 4 C) 3 D) 2
Punkt 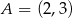 jest wierzchołkiem trójkąta równobocznego
jest wierzchołkiem trójkąta równobocznego 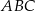 . Punkt
. Punkt 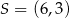 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie 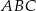 . Wskaż równanie okręgu wpisanego w trójkąt
. Wskaż równanie okręgu wpisanego w trójkąt 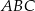 .
.
A) 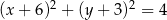 B)
B) 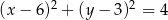
C) 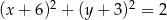 D)
D) 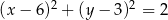
Punkt 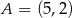 jest wierzchołkiem trójkąta równobocznego
jest wierzchołkiem trójkąta równobocznego 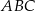 . Punkt
. Punkt 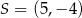 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie 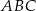 . Wskaż równanie okręgu wpisanego w trójkąt
. Wskaż równanie okręgu wpisanego w trójkąt 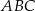 .
.
A) 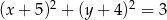 B)
B) 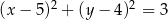
C) 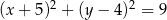 D)
D) 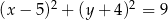
Miejscem zerowym funkcji 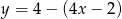 jest:
jest:
A) 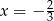 B)
B) 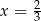 C)
C) 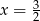 D)
D) 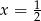
Miejscem zerowym funkcji liniowej 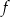 określonej wzorem
określonej wzorem 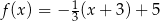 jest liczba
jest liczba
A) 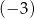 B)
B)  C) 5 D) 12
C) 5 D) 12
Miejscem zerowym funkcji 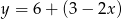 jest:
jest:
A) 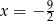 B)
B) 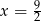 C)
C) 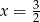 D)
D) 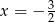
Funkcja liniowa określona jest wzorem 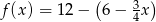 . Miejscem zerowym funkcji
. Miejscem zerowym funkcji 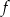 jest
jest
A) 8 B)  C)
C) 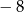 D)
D) 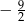
Cenę pewnego towaru obniżono najpierw o 30%, a potem o 50%. Początkowa cena została więc ostatecznie obniżona o 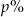 . Wynika stąd, że
. Wynika stąd, że
A) 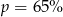 B)
B) 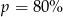 C)
C) 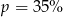 D)
D) 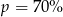
Cenę książki obniżano dwukrotnie, najpierw o 10%, a po miesiącu jeszcze o 5%. W wyniku obu obniżek cena książki zmniejszyła się o
A) 14% B) 14,5% C) 15% D) 15,5%
Cenę towaru obniżano dwa razy. Pierwsza obniżka wynosiła 10%, a druga 20%. O ile procent w wyniku obu obniżek spadła cena towaru?
A) o 24% B) o 26% C) o 28% D) o 30%
Cenę pewnego towaru podwyższono najpierw o 20%, a potem jeszcze o 10%. Rzeczywista podwyżka w procentach wyniosła
A) 20% B) 30% C) 32% D) 34%
Cena towaru została podwyższona o 30%, a po pewnym czasie nową, wyższą cenę ponownie podwyższono, tym razem o 10%. W rezultacie obu podwyżek wyjściowa cena towaru zwiększyła się o
A) 15% B) 20% C) 40% D) 43%
Cenę pewnego towaru obniżono najpierw o 20%, a potem o 30%. Początkowa cena została więc ostatecznie obniżona o 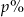 . Wynika stąd, że
. Wynika stąd, że
A) 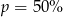 B)
B) 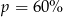 C)
C) 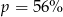 D)
D) 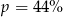
Cenę biurka obniżono o 10%, a następnie nową cenę obniżono o 30%. W wyniku obu tych zmian cena biurka zmniejszyła się w stosunku do ceny sprzed obu obniżek o
A) 43% B) 40% C) 37% D) 63%
Cenę nart obniżono o 20%, a po miesiącu nową cenę obniżono o dalsze 30%. W wyniku obniżek cena nart zmniejszyła się o
A) 44% B) 50% C) 56% D) 60%
Cenę pewnego towaru obniżono o 20%, a następnie nową cenę tego towaru obniżono o 30%. Takie dwie obniżki ceny tego towaru można zastąpić równoważną im jedną obniżką
A) o 50% B) o 56% C) o 44% D) o 66%
Cenę drukarki obniżono o 20%, a następnie nową cenę obniżono o 10%. W wyniku obu tych zmian cena drukarki zmniejszyła się w stosunku do ceny sprzed obu obniżek o
A) 18% B) 28% C) 30% D) 72%
Cenę komputera obniżano dwukrotnie, najpierw o 20%, a po miesiącu jeszcze o 10%. W wyniku obu obniżek cena komputera zmniejszyła się o
A) 31% B) 30% C) 29% D) 28%
Cenę pewnego towaru obniżano dwukrotnie, za każdym razem o 20%. Takie dwie obniżki ceny tego towaru można zastąpić równoważną im jedną obniżką
A) o 40% B) o 36% C) o 32% D) o 28%
Cenę pewnego towaru podwyższono o 20%, a następnie nową cenę tego towaru podwyższono o 30%. Takie dwie podwyżki ceny tego towaru można zastąpić równoważną im jedną podwyżką
A) o 50% B) o 56% C) o 60% D) o 66%
Cenę książki obniżono o 20%, a po miesiącu nową cenę obniżono o dalsze 10%. W wyniku obu obniżek cena książki zmniejszyła się o
A) 25% B) 28% C) 29% D) 30%
Cenę pewnego towaru podwyższono najpierw o 10%, a potem jeszcze o 10%. Rzeczywista podwyżka w procentach wyniosła
A) 20% B) 21% C) 22% D) 10%
Cenę pewnego towaru obniżono najpierw o 40%, a potem o 70%. Początkowa cena została więc ostatecznie obniżona o 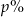 . Wynika stąd, że
. Wynika stąd, że
A) 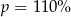 B)
B) 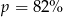 C)
C) 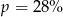 D)
D) 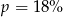
Funkcja kwadratowa 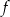 jest określona wzorem
jest określona wzorem 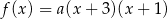 . Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Jednym z punktów tej paraboli jest punkt
. Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Jednym z punktów tej paraboli jest punkt 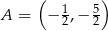 .
.
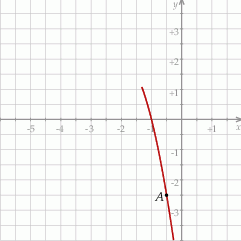
Współczynnik  we wzorze funkcji
we wzorze funkcji 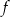 jest równy
jest równy
A) 1 B) 2 C) 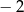 D)
D) 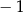
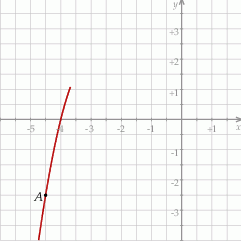
Funkcja kwadratowa 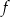 jest określona wzorem
jest określona wzorem 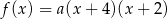 . Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Jednym z punktów tej paraboli jest punkt
. Na rysunku przedstawiono fragment paraboli będącej wykresem tej funkcji. Jednym z punktów tej paraboli jest punkt 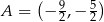 .
.
Współczynnik  we wzorze funkcji
we wzorze funkcji 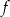 jest równy
jest równy
A) 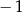 B)
B) 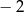 C) 2 D) 1
C) 2 D) 1
Granica 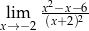
A) nie istnieje B) jest równa 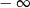 C) jest liczbą rzeczywistą D) jest równa
C) jest liczbą rzeczywistą D) jest równa 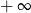
Granica 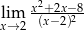
A) nie istnieje B) jest równa 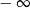 C) jest liczbą rzeczywistą D) jest równa
C) jest liczbą rzeczywistą D) jest równa 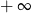
Granica 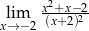
A) jest równa 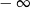 B) jest równa
B) jest równa 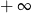 C) jest liczbą rzeczywistą D) nie istnieje
C) jest liczbą rzeczywistą D) nie istnieje
Granica 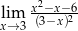
A) jest równa 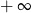 B) jest równa
B) jest równa 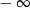 C) nie istnieje D) jest liczbą rzeczywistą
C) nie istnieje D) jest liczbą rzeczywistą
Granica 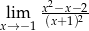
A) jest równa 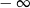 B) jest liczbą rzeczywistą C) nie istnieje D) jest równa
B) jest liczbą rzeczywistą C) nie istnieje D) jest równa 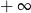
Granica 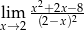
A) jest liczbą rzeczywistą B) nie istnieje C) jest równa 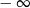 D) jest równa
D) jest równa 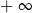
Granica 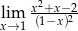
A) nie istnieje B) jest równa 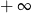 C) jest liczbą rzeczywistą D) jest równa
C) jest liczbą rzeczywistą D) jest równa 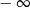
Granica 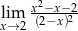
A) nie istnieje B) jest równa 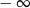 C) jest liczbą rzeczywistą D) jest równa
C) jest liczbą rzeczywistą D) jest równa 
Funkcja wykładnicza określona wzorem 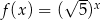 przyjmuje wartość 2 dla argumentu
przyjmuje wartość 2 dla argumentu
A) 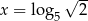 B)
B) 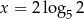 C)
C) 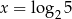 D)
D) 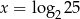
Funkcja wykładnicza określona wzorem 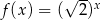 przyjmuje wartość 3 dla argumentu
przyjmuje wartość 3 dla argumentu
A) 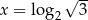 B)
B) 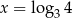 C)
C) 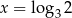 D)
D) 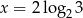
Obrazem trójkąta 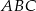 w podobieństwie o skali
w podobieństwie o skali 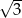 jest trójkąt
jest trójkąt 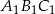 . Pole trójkąta
. Pole trójkąta 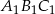 wynosi
wynosi 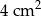 . Zatem pole trójkąta
. Zatem pole trójkąta 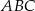 jest równe
jest równe
A) 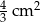 B)
B) 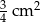 C)
C) 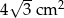 D)
D) 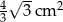
Pole trójkąta 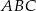 jest równe
jest równe 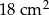 . Trójkąt
. Trójkąt 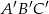 jest podobny do trójkąta
jest podobny do trójkąta 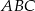 w skali
w skali 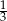 . Pole trójkąta
. Pole trójkąta 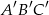 jest równe
jest równe
A) 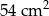 B)
B) 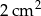 C)
C) 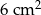 D)
D) 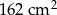
Pole trójkąta 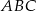 jest równe
jest równe 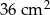 . Trójkąt
. Trójkąt 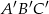 jest podobny do trójkąta
jest podobny do trójkąta 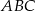 w skali
w skali 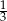 . Pole trójkąta
. Pole trójkąta 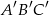 jest równe
jest równe
A) 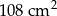 B)
B) 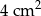 C)
C) 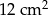 D)
D) 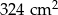
Trójkąt 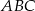 jest podobny do trójkąta
jest podobny do trójkąta 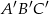 w skali
w skali  , przy czym
, przy czym 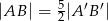 . Stosunek pola trójkąta
. Stosunek pola trójkąta 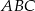 do pola trójkąta
do pola trójkąta 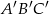 jest równy
jest równy
A) 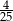 B)
B)  C)
C)  D)
D) 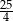
Obrazem trójkąta 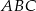 w podobieństwie o skali
w podobieństwie o skali 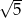 jest trójkąt
jest trójkąt 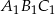 . Pole trójkąta
. Pole trójkąta 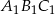 wynosi
wynosi 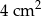 . Zatem pole trójkąta
. Zatem pole trójkąta 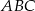 jest równe
jest równe
A) 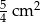 B)
B) 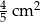 C)
C) 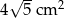 D)
D) 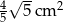
Obrazem trójkąta 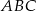 w podobieństwie o skali
w podobieństwie o skali 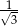 jest trójkąt
jest trójkąt 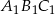 . Pole trójkąta
. Pole trójkąta 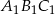 wynosi
wynosi 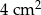 . Zatem pole trójkąta
. Zatem pole trójkąta 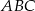 jest równe
jest równe
A) 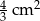 B)
B) 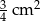 C)
C) 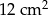 D)
D) 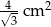
Ciąg geometryczny 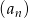 jest określony wzorem
jest określony wzorem 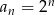 dla
dla 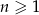 . Suma dziesięciu początkowych kolejnych wyrazów tego ciągu jest równa
. Suma dziesięciu początkowych kolejnych wyrazów tego ciągu jest równa
A) 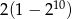 B)
B) 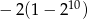 C)
C) 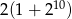 D)
D) 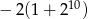
Ciąg geometryczny 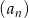 jest określony wzorem
jest określony wzorem 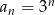 dla
dla 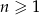 . Suma dziewięciu początkowych kolejnych wyrazów tego ciągu jest równa
. Suma dziewięciu początkowych kolejnych wyrazów tego ciągu jest równa
A) 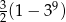 B)
B) 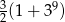 C)
C) 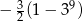 D)
D) 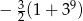
Wysokość 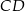 trójkąta równoramiennego
trójkąta równoramiennego 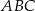 jest równa 8, a ramię
jest równa 8, a ramię 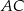 ma długość 10. Podstawa
ma długość 10. Podstawa 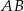 tego trójkąta ma długość
tego trójkąta ma długość
A) 12 B) 6 C) 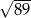 D)
D) 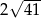
Wysokość 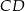 trójkąta równoramiennego
trójkąta równoramiennego 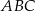 jest równa 10, a ramię
jest równa 10, a ramię 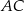 ma długość 14. Podstawa
ma długość 14. Podstawa 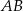 tego trójkąta ma długość
tego trójkąta ma długość
A) 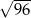 B)
B) 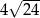 C)
C) 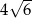 D)
D) 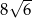
W trójkącie równoramiennym 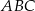 dane są
dane są 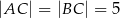 oraz wysokość
oraz wysokość 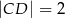 . Podstawa
. Podstawa 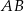 tego trójkąta ma długość
tego trójkąta ma długość
A) 6 B) 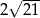 C)
C) 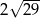 D) 14
D) 14
W trójkącie równoramiennym 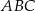 dane są
dane są 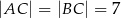 oraz wysokość
oraz wysokość 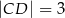 . Podstawa
. Podstawa 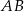 tego trójkąta ma długość
tego trójkąta ma długość
A) 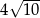 B)
B) 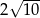 C)
C) 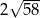 D) 10
D) 10
Do wykresu funkcji wykładniczej 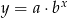 należą punkty
należą punkty 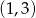 i
i 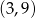 . Zatem liczba
. Zatem liczba 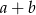 jest równa
jest równa
A) 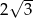 B) 12 C)
B) 12 C) 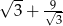 D)
D) 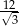
Do wykresu funkcji wykładniczej 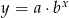 należą punkty
należą punkty 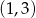 i
i 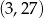 . Zatem liczba
. Zatem liczba 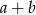 jest równa
jest równa
A) 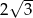 B) 12 C) 4 D)
B) 12 C) 4 D) 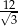
Po usunięciu jednej liczby z listy danych: 3, 2, 4, 1, 5, 1, 4, 1, 5, 2 średnia arytmetyczna zwiększyła się o 0,2. Którą liczbę usunięto z listy?
A) 1 B) 2 C) 3 D) 4
Po usunięciu jednej liczby z listy danych: 3, 2, 5, 4, 1, 5, 2, 4, 1, 5 średnia arytmetyczna zmniejszyła się o 0,2. Którą liczbę usunięto z listy?
A) 2 B) 3 C) 4 D) 5
Przedstawiony na rysunku wykres może być wykresem funkcji
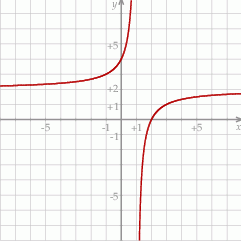
A) 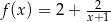 B)
B) 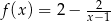 C)
C) 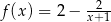 D)
D) 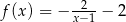
Przedstawiony na rysunku wykres może być wykresem funkcji
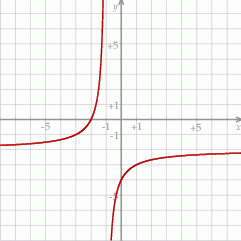
A) 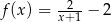 B)
B) 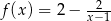 C)
C) 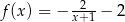 D)
D) 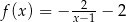
W ostrosłupie prawidłowym czworokątnym wszystkie krawędzie mają jednakową długość, a pole powierzchni całkowitej tego ostrosłupa jest równe 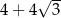 . Wobec tego długość wysokości tego ostrosłupa jest równa
. Wobec tego długość wysokości tego ostrosłupa jest równa
A) 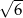 B) 2 C)
B) 2 C) 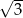 D)
D) 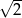
Jakim procentem koła jest pole wycinka koła zaznaczonego na rysunku?
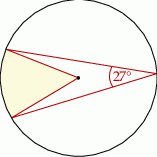
A) 7,5% B) 15% C) 20% D) 25%
Jakim procentem koła jest pole wycinka koła zaznaczonego na rysunku?
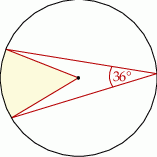
A) 7,5% B) 15% C) 20% D) 10%
Jakim procentem koła jest pole wycinka koła zaznaczonego na rysunku?
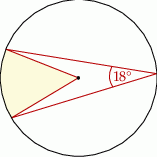
A) 5% B) 15% C) 20% D) 10%
Kąt  jest ostry i
jest ostry i 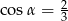 . Wartość wyrażenia
. Wartość wyrażenia 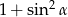 jest równa
jest równa
A) 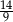 B)
B) 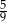 C)
C)  D)
D) 
Kąt  jest ostry i
jest ostry i 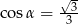 . Wtedy wartość wyrażenia
. Wtedy wartość wyrażenia 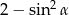 jest równa
jest równa
A) 0 B)  C)
C) 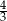 D) 1
D) 1
